Что такое дискретная непрерывность
Дискретная непрерывность и разрывы (Австралия)
Если какая-то целочисленная величина в процессе меняется на каждом шаге не больше чем на 1 (в ту или другую сторону), то она обязательно проходит через все промежуточные значения между начальным и конечным. Такая величина называется дискретной, а прием – дискретной непрерывностью..
1. В футбольном матче первым забил «Спартак», а выиграло «Торпедо». Докажите, что в какой то момент счет был ничейный.
2. В ряд выложены 200 шаров, из них 100 черных и 100 красных, причем первый и последний шары – черные. Докажите, что можно убрать с правого края несколько шаров подряд так, чтобы красных и черных шаров осталось поровну.
Полезно раскрасить объекты в два цвета так, чтобы граница или разрыв отделяли цвета.
3. В последовательности целых чисел каждое число, начиная со второго, на 1 больше предыдущего или в 3 раза меньше предыдущего. Первое число равно 1, последнее равно 100. Докажите, что среди чисел есть и 77. ( Могут быть и числа больше 100)
4. В ряд лежат 100 яблок, соседние отличаются не более чем на 10 г. Докажите, что если выложить яблоки в ряд по возрастанию веса, то и тогда соседние будут отличаться не более чем на 10 г.
Если процесса нет, организуй сам. Подбери начало и конец процесса так, чтобы они были по разные стороны от нужного значения.
5. В ряд сидит 15 мальчиков и 15 девочек.
а) Докажите, что можно выбрать 10 школьников подряд, чтобы среди них мальчиков и девочек было поровну.
б) Всегда ли из них можно выбрать 20 школьников подряд, среди которых мальчиков и девочек поровну?
6. а) По кругу сидят 30 школьников, среди них мальчиков и девочек поровну. Докажите, что можно выбрать 20 школьников подряд, чтобы среди них мальчиков и девочек было поровну.
б) По кругу сидят 30 школьников, среди них мальчиков и девочек поровну. Докажите, что можно выбрать 18 школьников подряд, чтобы среди них мальчиков и девочек было поровну.
7. На клетчатой доске 100×100 стоит 3000 шашек. Докажите, что где бы они не стояли, доску можно разрезать по границам клеток на три части, в каждой из которых будет по 1000 шашек.
В некоторых процессах полезно начало и конец поменять местами. Тут помогает расположение на окружности.
8. На клетчатой рамке 100×100 толщиной в одну клетку стоит 150 шашек. Докажите, что рамку можно разрезать по границам клеток на две равные части с равным количеством шашек.
9. На клетчатой доске 100×100 стоит 1000 шашек. Докажите, доску можно разрезать по границам клеток на две равные части с равным количеством шашек.
Задачи посложнее сводятся к типовым с помощью приёма «засада на переправе»: показывается, что нужный результат достигается в момент прохода дискретной величины через определённое значение.
10. У Кости была кучка из 100 камешков. Каждым ходом он делил какую-то из кучек на две меньших, пока у него в итоге не оказалось 100 кучек по одному камешку. Докажите, что в какой-то момент в каких-то 30 кучках было в сумме ровно 60 камешков.
Московские сборы, 9 класс, А. Шаповалов www. ashap. info 7 апреля 2013 г.
Дискретная непрерывность. Домашнее задание (Австралия)
ДН1. В ряд стоят несколько солдат. Рост соседей отличается не более чем на 2,4 см.
а) В строю есть солдат ростом 152 см, и солдат ростом 198 см. Докажите, что есть солдат, чей рост отличается от 170 см не более, чем на 1,2 см.
б) Докажите, что если солдаты встанут по росту, то по-прежнему рост соседей будет отличаться не более, чем на 2,4 см.
ДН3. В бесконечной последовательности натуральных чисел каждое следующее число получается прибавлением к предыдущему одной из его ненулевых цифр. Докажите, что в этой последовательности найдется четное число.
ДН4. За круглым столом равномерно посажены 100 дедов, причем у любых двух соседей количество волос в бородах отличается не больше, чем на 100. Докажите, что найдется пара дедов, сидящих напротив друг друга, у которых количество волос в бородах также отличается не больше, чем на 100.
ДН5’. В строке шестизначных чисел первое число последнее 654321. Соседние числа отличаются на 1 или на 1000. Ни одно число не делится на 1000. Докажите, что хотя бы одно число делится на 13.
ДН6. В одном из 100 окопов, расположенных в ряд, спрятался робот-пехотинец. Автоматическая пушка может одним выстрелом накрыть любой окоп. В каждом промежутке между выстрелами робот (если уцелел) обязательно перебегает в соседний окоп (быть может, только что обстрелянный).
а) Известно, что вначале слева от робота – нечетное число пустых окопов. Сможет ли пушка наверняка накрыть робота?
б) Вначале робот может быть в любом из окопов. Сможет ли пушка наверняка накрыть робота?
ДН7. Дракон заточил рыцаря в темницу и выдал ему 100 различных монет, половина из которых – фальшивые (но какие именно – знает только дракон). Каждый день рыцарь раскладывает монеты на две кучки (не обязательно равные). Если в какой-то день в этих кучках окажется поровну настоящих монет, либо поровну фальшивых, то дракон отпустит рыцаря. Сможет ли рыцарь гарантированно освободиться не позже, чем на двадцать пятый день?
Дискретность в физике и математике. Лекция. Катющи
Дискретный простыми словами – прерывный, разделенный, зернистый, отдельный
— свойство, противопоставляемое непрерывности.
Каждый способен отличить прерывное от непрерывного.
Но если смотреть глубже, то дискретность можно разделить на наружную и внутреннюю.
И гранат например имеет внутреннюю дискретность (состоит из отдельных зёрен), а так же сам может быть рассмотрен как отдельное зерно. На своей поверхности гранат прервался и дальше уже не гранат.
И когда мы например, говорим: «Маша мыла раму», мы должны четко понимать, что Маша так же имеет наружную дискретность – то есть: имеет самостоятельный внешний контур – является самостоятельным объектом.
Так же Маша имеет внутреннюю дискретность – состоит из клеточек. И швабра у Маши так же имеет и внешнюю и внутреннюю дискретность.
И здесь тоже все просто.
Но есть определенные подробности и у многих людей с недискретным, с непрерывным возникают трудности. Попробуем пояснить почему.
Представьте человека, который вырос в глухой степи и по случайному стечению обстоятельств ему никто не рассказал про экскаватор.
И единственное что у него в голове срабатывает:
— Это какие же здесь суслики водятся, что они такую яму вырыли.
И есть вполне конкретные типы задач, который в определенном смысле навязывает воображаемого кимберлитового суслика.
В этом списке и задача на дискретность.
И опять же накладываются представления, что все что нас окружает – состоит из атомов, имеет корпускулярную сущность.
Например, стена её можно пощупать и мы воспринимаем её относительную непрерывность, но жизненный опыт показывает, что у этой непрерывности должен быть внешний край, конец, а значит и стена какая бы длинная она не была в конечном итоге дискретна ( и сама по себе это тоже отдельный элемент). То есть непрерывность (на примере стены) конечна – имеет место наружная дискретность, наружная прерывность.
Следующая позиция №4
Непрерывность материальная, но не вещественная.
Что у нас в природе вообще есть материальное, но не вещественное?
И что материальное может быть фундаментально непрерывным?
И применительно к полю ряд людей вновь, сами не понимая почему – готовы сделать выбор в пользу дискретного решения.
Человеку просто кажется, что и в этом случае неизменно должны быть какие-то дискретные штуки.
В этих случаях помочь не всегда возможно, но на всякий случай сообщаем.
Справочно:
Кимберлитовые суслики не внесены в красную книгу
не находятся под защитой здравого смысла и их можно смело утилизировать.
Для остальных просто напомним, что поле не имеет массы, не имеет вещественности. У поля нет той самой штуки которая может обеспечить внутреннюю дискретность.
Так же у поля нет наружной дискретности. Потому что поле не ограничивается с расстоянием.
И это мы можем наглядно продемонстрировать через график распределения поля в пространстве.
Если мы расположим в пространстве некий единичный источник воздействия, и окружим его некой сферой, то с расширением этой сферы её площадь будет увеличиваться и следовательно будет уменьшаться доля воздействия выпадающая на единицу площади этой сферы.
Формульно это выражается через площадь поверхности сферы
А поскольку речь идет о рассеивании единичного воздействия на поверхность сферы то мы имеем единицу деленную на площадь поверхности сферы, то есть
данное распределение воздействия соответствует приведенному графику.
И в связи с эти мы должны понимать, что даже поле от маленького комаринного магнитика распространяется бесконечно далеко и не имеет внешних границ.
При этом по мере удаления потенциал поля стремится к нулю но никогда через этот нуль не переходит.
Итого применительно к физике мы можем выделить 4 вида дискретных и недискретных состояний.
позиция №1
— Наружная дискретность. Присуща материи разделенной на отдельные фрагменты. Материя имеющая внешние границы.
Позиция № 2
— внутренняя дискретность в рамках некой непрерывности
— присуща материи имеющей общую протяженную вещественную непрерывность, и внутреннее дискретное строение в форме отдельных элементов.
В эту категорию попадают все объекты состоящие из вещества, которые внешне воспринимаются как непрерывные, но по своей структуре состоят из более мелких частей.
Позиция № 3
непрерывность нематериальная (присущая пространству) не имеющая внутренней структуры (внутренней дискретности).
позиция №4
Непрерывность материальная невещественная (присущая физическому полю).
Данные четыре позиции желательно твёрдо запомнить. Это облегчит понимание физики в целом.
Собственно всё.
С вами был Виктор Катющик.
Подписывайтесь на видеоканал.
Следите за нашими публикациями.
Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.
Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
Далее проанализируем особенности применения термина в различных областях.
Дискретная математика
Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.
ДМ условно подразделяется на пять направлений:
Дискретная величина
Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.
Дискретность в информатике
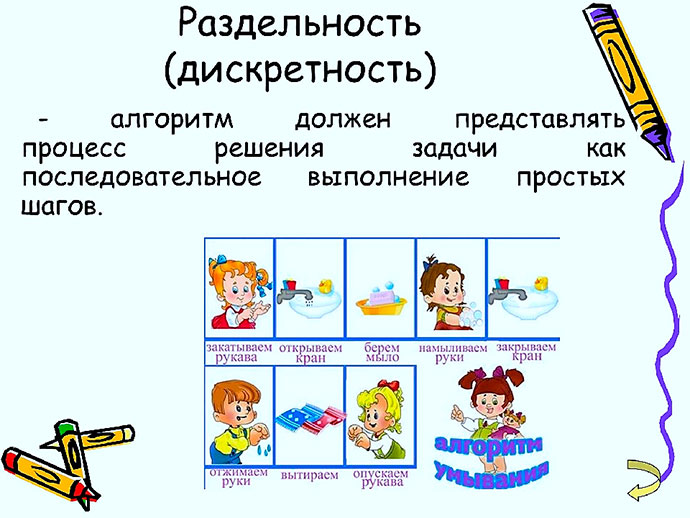
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).
Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.
Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):
Дискретная видеокарта
Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.
Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.
Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.
Дискретность в биологии
Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Благодарю за дискретное изложение материала
Что такое дискретная непрерывность
3. На базе диалектической логики возможен синтез этих подходов, и он характерен для современной науки. Но об этом – ниже.
Гипотеза о Д. времени занимает важное место в атомистике древних. Об этом рассказывает Аристотель. По-видимому, время у них складывается из ничтожных по длительности и больше неделимых мгновений. Вместе они образуют моменты единого для всего мира «настоящего времени» или «теперь». События, происшедшие в одно и то же мгновение, – одновременны. Фактически, это была первая версия т.н. «абсолютного времени». Изначально, в основе этого атомизма лежала идея о тождестве строения макро- и микрокосмоса: природа, будучи единой, должна быть устроена и в малейшей своей части так же, как и в величайшей. Эта идея в ХХ веке воплотилась сначала в планетарной модели атома Э.Резерфорда (1871-1937). Она стала основой и системно-структурного фундаментализма ХХ века (как у А.А.Богданова в его тектологии и Л.фон Берталанфи и др. в общей теории систем, в органицизме). Однако научное открытие атомов вещества произошло раньше всего в химии.
3) Химический атомизм, опираясь на взгляды Ньютона, создал впервые в Англии Дж.Дальтон (1766-1844). Он ввел представление об атомном весе, специфическом для каждого сорта атомов вещества. Атом в химии – самая маленькая порция вещества определенного вида. Появилось представление о молекулах как сочетании атомов, образующих все многообразие вещества в природе. Единицей атомного веса стал атом водорода. Впоследствии эти результаты привели русского химика Д.И.Менделеева (1834-1907) к созданию знаменитой химической периодической «системы Менделеева», обладавшей большими эвристическими возможностями для открытия новых и новых элементов. В XIX веке усилиями А.Купера и Ф.Кекуле была развита идея валентности, объяснение которой, как и химизма вообще, осуществила уже физика в атомной теории Н.Бора (1885-1962). Между тем, происходит познание новых видов движений и соответствующих им законов. Мы сегодня уже хотим узнать верхние и нижние границы химизма (например, есть ли т.н. “остров стабильности” в районе 120 номера таблицы Менделеева). Сейчас возникли вопросы о влиянии на наш мир темной материи и движения, роли нейтрино в рамках этой материи и др. вопросы.
По определению, Н. – неразрывная связь в бытии или переход в его становлении. Здесь действует закон, установленный Г.Лейбницем: «природа не делает скачков», ибо в ней все процессы сплошь состоят из скачков, и что в ней нет никаких пробелов и все связано благодаря переходам (см.: Непрерывность // Краткая философская …, с. 299-300). Вряд ли можно считать, что квантовая теория, где квант – атом энергии, оправдывает абсолютность квантования для всего микромира: каждый кантовый скачок в состояния электронов в атоме все-таки не происходит с бесконечно большой скоростью. Это вроде бы запрещено принципами релятивистской физики, кроме того, мы не знаем, что в это же время происходит с темной энергией и в её «среде».
Естествознание. 10 класс
Конспект урока
Естествознание, 10 класс
Урок 11. Дискретность и непрерывность в природе
Перечень вопросов, рассматриваемых в теме: В чем суть дискретной и непрерывной концепции строения материи? Как с позиций дискретного и непрерывного подходов описываю различные природные объекты? Что такое поле? Для описания каких объектов применяют понятие поля? Как наглядно можно изобразить поле?
Континуальная концепция – концепция, согласно которой материя непрерывна (делима до бесконечности).
Корпускулярная концепция – концепция, согласно которой материя имеет дискретную (прерывистую) структуру и состоит из отдельных, предельно малых частиц.
Скалярное поле – область пространства, в каждой точке которой определено числовое значение некоторой величины.
Векторное поле – область пространства, в каждой точке которого задан вектор с началом в данной точке.
Основная и дополнительная литература по теме урока:
1. Естествознание. 10 класс: учебник для общеобразоват. организаций: базовый уровень / И.Ю. Алексашина, К.В. Галактионов, И.С. Дмитриев, А.В. Ляпцев и др. / под ред. И.Ю. Алексашиной. – 3-е изд. – М.: Просвещение, 2017. – С. 50-52.
2. Энциклопедия для детей. Том 16. Физика. Ч. 1. Биография физики. Путешествие в глубь материи. Механическая картина мира / Глав. ред. В.А. Володин. – М.: Аванта+, 2000. – С. 37-40, 342-350.
3. Эйнштейн А., Инфельд Л. Эволюция физики: развитие идей от первоначальных понятий до теории относительности и квантов / А. Эйнштейн, Л. Инфельд. – СПб.: Амфора, 2013. – С. 200-203.
Открытые электронные ресурсы по теме урока
Новая философская энциклопедия. Непрерывность и прерывность. URL:
Теоретический материал для самостоятельного изучения
Понятие материи является ключевым для естествознания. Два противоположных представления о структуре материального мира возникли в рамках античных натурфилософских учений. Представления о непрерывности, внутренней однородности, целостности материи, заполняющей собой всё пространство и не оставляющей пустоты, лежат в основе континуальной концепции (Аристотель). Согласно этой концепции деление материи возможно до бесконечности. Пространство и время рассматривалось как особый вид отношений между материальными объектами. Представления о дискретности пространственно-временного строения материи, лежат в основе корпускулярной (атомистической) концепции (Демокрит). Согласно атомистике деление материи возможно до определённого предела – мельчайших частиц (атомов), движение которых не возможно без существования пустоты.
Развитие научного познания попеременно приводило к укреплению позиций то одной, то другой концепции. Так вплоть до XVII века господствующее положение занимали континуальные представления в изложении Аристотеля. Создание И. Ньютоном основ классической механики серьезно укрепило позиции корпускулярной концепции. В то же время представление о непрерывности материи нашло свое отражение в развитии концепции эфира и волновой оптики (Р. Декарт, Х. Гюйгенс). Создание во второй половине XIX века Дж. Максвеллом теории электромагнитного поля выдвинуло на передовые позиции континуальную концепцию. Современные представления о природе микрообъектов сочетают обе концепции, что нашло свое отражение в принципе корпускулярно-волнового дуализма.
Представления о дискретности и непрерывности материального мира лежат в основе двух подходов к описанию природных объектов. Каждый из подходов использует определенные математические средства и позволяет получить различные наглядные изображения описываемого объекта. Здесь следует напомнить о роли математики в естественных науках. Одним из важнейших математических понятий является функция. С ее помощью выражают зависимость между переменными величинами. Так, описывая движение материальной точки, мы учитывать зависимость ее координат от времени, т.е. координаты определяются как функции от времени x=x(t), y=y(t), z=z(t).
Корпускулярное описание. Описываемый объект рассматривается как дискретный, состоящий из отдельных частей. Для каждой из частей объекта задаются различные параметры. Тогда, совокупность заданных для всех частей объекта параметров и будет описанием данного объекта. Так, при описании Солнечной системы каждую из планет рассматривают как материальную точку, которой задаются координаты как функции от времени. Обозначим совокупность всех координат в некоторой системе отсчета как
Для описания, например, течения воды корпускулярный подход невозможен, слишком большое число молекул воды требуется описать. Для протяженных объектов используется континуальный подход, основывающийся на идеях непрерывности материи.
При континуальном описании используется такое математическое понятие как поле. Под полем будем понимать область в пространстве, в каждой точке которой определено значение некоторой величины. Если в каждой точке пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Так если провести некоторую плоскость над поверхностью земли и задать систему координат, а каждой точке М(х,у) фрагмента этой плоскости поставить в соответствие температуру, то получим поле температуры. Так как температура величина скалярное, то и такое поле называется скалярным. Скалярные поля задаются функциями от координат. Примерами скалярных полей являются поля давления, плотности, высоты над уровнем моря и т.д. Для векторных величин, которые характеризуются не только числовым значением, но и направлением, задают векторное поле. Векторное поле – это область пространства, в каждой точке которого задан вектор с началом в данной точке. Примером векторного поля может служить магнитное поле Земли.
Приведем еще примеры. Чтобы дать характеристику лесу, которая была бы полезна лесозаготовителям, можно рассмотреть среднее количество деловой древесины в м 3 на квадратный километр леса в определенном районе. Обозначим эту величину за М и введем координаты x и y, так как эта величина зависит от конкретного района. Зависимость величины М от координат обозначим как функцию М (x,y). Поскольку число деревья в лесу меняется: одни растут, другие могут погибнуть, необходимо учесть зависимость от времени М (x,y,t). Функция М (x,y,t) представляет собой скалярное поле, характеризующее плотность деловой древесины в лесу.
При описании рельефа земной поверхности используют поле высоты над уровнем моря или глубины океана. На географических картах это обычно изображают цветом. Математически данные характеристики можно описать как функции h(ϕ,θ) где ϕ и θ географическая широта и долгота. На топографических картах скалярное поле высоты над уровнем моря изображают как линии равных высот для обозначения холмов и впадин.
Для того, чтобы охарактеризовать течение воды в различных точках водных объектов, необходимо знать скорость 
, с которой перемещается вода в данной точке. Т.е. необходимо задать функцию скорости от координат 
(x,y,z), а если еще учесть зависимость от времени, то 
(x,y,z,t). Напомним, что скорость величина векторная. Функция 
(x,y,z,t) представляет собой векторное поле, характеризующее скорость течения жидкости. Изобразить векторное поле можно с помощью векторных линий. Так, для поля скоростей текущей жидкости векторные линии – это траектории, по вдоль которых движутся частицы жидкости. Скорость воды в любой точке траектории направлена по касательной к ней. Наглядным изображением такого векторного поля являются линии течений, которые стрелками изображаются на географических картах.
Описание природных объектов основывается на двух противоположных подходах, отражающих представления о дискретности или непрерывности материи. Корпускулярное описание объекта заключается в задании различных параметров, характеризующих каждую из его составляющих частей. Если параметры зависят от времени, то учитывается и эта зависимость. При континуальном описании протяжённых объектов используют понятие поля, под которым понимается некоторая характеристика объекта, выраженная как функция от координат и времени. Поля наглядно можно изобразить на плоскости в виде линий. Скалярное поле изображается линиями постоянного значения поля. Для векторного поля направленные линии проводятся так, что в каждой точке линии вектор, соответствующий полю в данной точке, будет касательным к линии.
Примеры и разбор решения заданий тренировочного модуля:
1. Укажите верные утверждения:
Правильный ответ и пояснение
А. Чтобы описать объект с позиций корпускулярного подхода, необходимо задать параметры для каждой из составных частей объекта.
Правильное утверждение. При корпускулярном подходе объект рассматривается как состоящий их отдельных частей, поэтому задают параметры для каждой из них.
Б. Изобары (линии, соединяющие места одинакового атмосферного давления) на картах погоды соответствуют векторному полю.
Неправильное утверждение. Давление величина скалярная, а скалярным величинам соответствуют скалярные поля.
В. Чтобы описать объект с позиций континуального подхода, необходимо задать поле величины, характеризующей объект.
Правильное утверждение. При континуальном подходе объект рассматривается как непрерывный и для его описания используют поля определенных величин.
Г. Поле скоростей жидкости, изображенное на географических картах как линии течений, является скалярным полем.
Неправильное утверждение. Скорость – величина векторная, то поле скорости – векторное поле.
Д. Корпускулярный подход используется при описании движения тел в рамках классической механики.
Правильное утверждение. Классическая механика основывается на корпускулярной концепции строения материи.
Правильный ответ: А, В, Д.
2. Установление соответствие между элементами двух множеств. К каждой позиции первого столбца подберите соответствующую позицию второго.
Наглядное изображение поля
1.Линии равных высот на топографических картах
2. Линии течений на географических картах
3. Линии равных средних годовых температур на климатических картах
Правильный ответ: 1 – А; 2 – Б; 3 – А.
Пояснения: Скалярным величинам задают скалярные поля, векторным – векторные поля Высота и температура – скалярные величины, а скорость течения воды – векторная (характеризуется направлением).