Что такое динамика в механике
Техническая механика
Динамика
Основные понятия и аксиомы динамики
Динамика есть часть теоретической механики, изучающая механическое движение тел в зависимости от сил, влияющих на это движение.
Динамика основывается на ряде положений, которые являются аксиомами и называются законами динамики.
Прежде чем перейти к рассмотрению этих законов, необходимо раскрыть сущность понятий материальной точки и изолированной материальной точки.
Под материальной точкой подразумевают некое тело, имеющее определенную массу (т. е. содержащее некоторое количество материи), но не имеющее линейных размеров (бесконечно малый объем пространства).
Изолированной считается материальная точка, на которую не оказывают действие другие материальные точки.
В реальном мире изолированных материальных точек, как и изолированных тел, не существует, это понятие является условным.
Первый закон Ньютона (первый закон динамики)
В кинематике было установлено, что прямолинейное равномерное движение является единственным видом движения, при котором ускорение равно нулю, поэтому аксиому инерции можно сформулировать следующим образом: ускорение изолированной материальной точки равно нулю.
Второй закон Ньютона (второй закон динамики)
Следовательно, для данной материальной точки отношение любой силы к вызываемому ею ускорению есть величина постоянная. Эту величину (отношение силы к ускорению) называют массой материальной точки, и обозначают ее m :
Что такое масса тела
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства. Ньютон называл массой количество материи, заключенной в теле, считая массу каждого тела величиной постоянной.
Современное представление о мире, после открытий, совершенных А. Эйнштейном, опровергает этот вывод И. Ньютона – масса не является постоянной величиной для тела, она зависит от скорости, с которой это тело движется. Так, например, наблюдения за движением заряженных частиц в ускорителях показали, что инертность частицы (т. е. способность сохранять свою скорость) возрастает с увеличением ее скорости.
Теория относительности устанавливает следующую зависимость между массой тела, находящегося в покое, и массой движущегося тела:
где m – масса движущегося тела, m0 – масса покоящегося тела (масса покоя), v = скорость движения тела, c – скорость света.
Из этой формулы видно, что чем больше скорость движения тела, тем больше его масса и, следовательно, тем труднее сообщить ему дальнейшее ускорение. При скоростях близких к скорости света масса тела стремится к бесконечности, и для дальнейшего ускорения такого тела требуется сила бесконечной величины.
Очевидно, что материальное тело не может двигаться со скоростью света, поскольку не существует реальная сила, способная ускорить его до такого состояния.
Второй закон Ньютона выражается равенством:
Ускорение свободного падения
Опытным путем установлено, что под действием притяжения Земли в вакууме тела падают с одинаковым ускорением, которое называется ускорением свободного падения.
т. е. силы тяжести тел пропорциональны их массам, что позволяет сравнивать массы различных тел путем взвешивания (сравнивания их сил тяжести при помощи весов).
Из второго закона Ньютона следует, что под действием постоянной силы находившаяся в покое свободная материальная точка движется прямолинейно равнопеременно (с постоянным ускорением).
Движение под действием постоянной силы может быть и прямолинейным и криволинейным (в последнем случае материальная точка имеет начальную скорость, вектор которой не совпадает с вектором силы). Пример движения под действием постоянной силы – свободное падение тел.
Третий закон Ньютона
К основным законам динамики относится и рассмотренная в Статике аксиома взаимодействия, или третий закон Ньютона.
Применительно к материальной точке закон формулируется так: силы взаимодействия двух материальных точек по модулю равны между собой и направлены в противоположные стороны (действие равно противодействию).
На основании этого закона можно сделать вывод, что сила, как мера взаимодействия между телами, не может проявляться без пары, т. е. если возникает какое-либо силовое воздействие, то существует и «двойник» этого силового воздействия, равный по модулю и противоположный по вектору.
Тема 3.1. Основные понятия и аксиомы динамики
§1. Динамика точки. Основные понятия и определения.
В разделе кинематики исследовалось движение тел без учета причин, обеспечивающих это движение. Рассматривалось движение, заданное каким-либо способом и определялись траектории, скорости и ускорения точек этого тела.
В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.
Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.
Понятие о силе, как о величине, характеризующей меру механического взаимодействия материальных тел, было введено в статике. Но при этом в статике мы, по существу, считали все силы постоянными. Между тем, на движущееся тело наряду с постоянными силами (постоянной, например, можно считать силу тяжести) действуют обычно силы переменные, модули и направления которых при движении тела изменяются.
Сила – векторная физическая величина, характеризующая действие одного тела на другое, в результате чего у тела изменяется скорость, то есть появляется ускорение, или происходит деформация тела, либо имеет место и то, и другое. В том случае, когда тело при взаимодействии получает ускорение, говорят о динамическом проявлении сил. В том случае, когда тело при взаимодействии деформируется, говорят о статическом проявлении сил.
Как показывает опыт, переменные силы могут определенным образом зависеть от времени, от положения тела и от его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата; от положения тела зависит сила упругости пружины; от скорости движения зависят силы сопротивления среды (воды, воздуха).
К понятию об инертности тел мы приходим, сравнивая результаты действия одной и той же силы на разные материальные тела. Опыт показывает, что если одну и ту же силу приложить к двум разным, свободным от других воздействий покоящимся телам, то в общем случае по истечении одного и того же промежутка времени эти тела пройдут разные расстояния и будут иметь разные скорости.
Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.
Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.
За единицу массы принят эталон – сплав платины и иридия, хранящийся в палате мер и весов в Париже: [m]=кг. Масса–величина аддитивная
и скалярная.
В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т.е. от распределения масс).
Под материальной точкой понимают материальное тело столь малых размеров, что различием в движении отдельных его точек можно пренебречь и положение которого можно определить координатами одной из его точек.
Практически данное тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела при его движении, очень велики по сравнению с размерами самого тела. Кроме того, как будет показано в динамике системы поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.
Наконец, материальными точками можно считать частицы, на которые мы будем мысленно разбивать любое тело при определении тех или иных его динамических характеристик.
Точку будем называть изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется. Конечно, трудно привести пример подобного состояния. Но представить такое можно.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
§2. Законы динамики
В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные обширной общественно-исторической практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном.
Первый закон (закон инерции), открытый Галилеем, гласит: существуют такие системы отсчета, относительно которых тело покоится или движется прямолинейно и равномерно, если на него не действуют другие тела или действие этих тел компенсировано.
или в другой формулировке
если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое.
Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.
Основы механики для «чайников». Часть 2: Динамика
В чем сила, брат?
Красота – страшная сила! А еще, конечно, сила в правде, а у кого-то в деньгах. Но мы-то знаем, что все это заблуждения и домыслы. Сила – в Ньютонах!
Сила – векторная физическая величина, количественная мера интенсивности взаимодействия тел.
Единицей измерения силы в системе СИ является Ньютон. Один Ньютон – это такая сила, которую мы можем приложить к телу массой один килограмм. При этом она изменит скорость тела на 1 м/с за одну секунду.
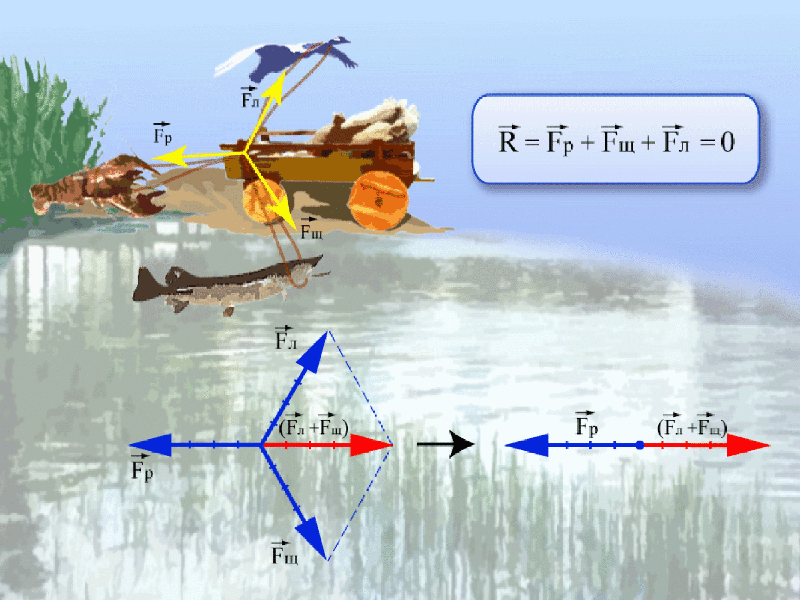
Например, на рисунке ниже равнодействующая сил равна нулю, потому как лебедь рак и щука так никуда и не сдвинули воз.
Масса и Вес
Масса – скалярная аддитивная физическая величина, являющаяся количественной мерой инертности тела, то есть его способности сохранять постоянную скорость.
В системе СИ измеряется в килограммах. Если не ищете легких путей и хотите быть особенно экстравагантным, можете измерять в фунтах, пудах и унциях.
Важно! Не стоит путать массу тела и вес. Ведь масса – скалярная величина, а вес – это сила, с которой тело действует на опору или подвес. Другими словами, масса всегда остается постоянной, это собственная характеристика тела. А вот вес может меняться. Например, Ваш лунный вес будет отличаться от земного, т.к. ускорение свободного падения на планетах различно.
Первый закон Ньютона
Как мы уже знаем, движение осуществляется в системе отсчета. Так вот, существуют такие системы отсчета, которые называются инерциальными (ИСО). Что это значит? Это тоже идеализация, наподобие материальной точки. Существование ИСО постулируется первым законом Ньютона, который собственно гласит вот что:
Существуют системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно или покоятся, если на них не действуют никакие силы, или действие других сил скомпенсировано (равнодействующая равна нулю).
Если в инерциальной системе отсчета мы разгоним автомобиль до скорости 60 км/ч, пренебрежем силой трения колес об асфальт и сопротивлением воздуха, а потом выключим двигатель, авто продолжит катиться по прямой со скоростью 60 км/ч бесконечно долго, пока не закончится дорога.
Второй закон Ньютона
Второй закон Ньютона еще называют основным законом динамики. Самая простая его формулировка такова:
В ИСО ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела.
Еще одна формулировка второго закона Ньютона: производная импульса материальной точки по времени равна действующей на материальную точку силе. Импульс – мера количества движения, равняется произведению массы на скорость.
Действительно, вспомним кинематику (производная от скорости равна ускорению) и запишем:
Третий закон Ньютона
В ИСО тела действуют друг на друга с силами, лежащими на одной прямой, противоположными по направлению и равными по модулю.
Напоследок, как всегда, приведем пример решения задачи на основы динамики.
Брусок массой 5кг тянут по горизонтальной поверхности за веревку, составляющую угол 30 градусов с горизонтом. Сила натяжения веревки – 30 Ньютонов. За 10 секунд, двигаясь равноускоренно, брусок изменил скорость с 2 м/с до 12 м/с. Найти коэффициент трения бруска о плоскость.
Нарисуем брусок. На него действуют сила тяжести, сила нормальной реакции опоры, сила трения и сила натяжения веревки. Веревку будем считать нерастяжимой. Первым делом найдем ускорение бруска, а затем вычислим проекцию сил на горизонтальную ось и запишем второй закон Ньютона.
Основы динамики в физике очень важны для понимания процесса движения. Помните, друзья, в экстремальных условиях сессии наши авторы всегда готовы поддержать Вас и облегчить учебную нагрузку. Удачи Вам!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Что такое динамика в механике
Если в кинематике только описывается движение тел, то в динамике изучаются причины этого движения под действием сил, действующих на тело.
Динамика – раздел механики, который изучает взаимодействия тел, причины возникновения движения и тип возникающего движения. Взаимодействие – процесс, в ходе которого тела оказывают взаимное действие друг на друга. В физике все взаимодействия обязательно парные. Это значит, что тела взаимодействуют друг с другом парами. То есть всякое действие обязательно порождает противодействие.
Сила – это количественная мера интенсивности взаимодействия тел. Сила является причиной изменения скорости тела целиком или его частей (деформации). Сила является векторной величиной. Прямая, вдоль которой направлена сила, называется линией действия силы. Сила характеризуется тремя параметрами: точкой приложения, модулем (численным значением) и направлением. В Международной системе единиц (СИ) сила измеряется в Ньютонах (Н). Для измерения сил используют откалиброванные пружины. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра.
Сила, оказывающая на тело такое же действие, как и все силы, действующие на него, вместе взятые, называется равнодействующей силой. Она равна векторной сумма всех сил, действующих на тело:
Чтобы найти векторную сумму нескольких сил нужно выполнить чертеж, где правильно нарисовать все силы и их векторную сумму, и по данному чертежу с использованием знаний из геометрии (в основном это теорема Пифагора и теорема косинусов) найти длину результирующего вектора.
Виды сил:
1. Сила тяжести. Приложена к центру масс тела и направлена вертикально вниз (или что тоже самое: перпендикулярно линии горизонта), и равна:
2. Сила трения. Приложена к поверхности соприкосновения тела с опорой и направлена по касательной к ней в сторону противоположную той, куда тянут, или пытаются тянуть тело другие силы.
3. Сила вязкого трения (сила сопротивления среды). Возникает при движении тела в жидкости или газе и направлена против скорости движения.
4. Сила реакции опоры. Действует на тело со стороны опоры и направлена перпендикулярно опоре от нее. Когда тело опирается на угол, то сила реакции опоры направлена перпендикулярно поверхности тела.
5. Сила натяжения нити. Направлена вдоль нити от тела.
6. Сила упругости. Возникает при деформации тела и направлена против деформации.
Обратите внимание и отметьте для себя очевидный факт: если тело находится в покое, то равнодействующая сил равна нулю.
Проекции сил
В большинстве задач по динамике на тело действует больше чем одна сила. Для того чтобы найти равнодействующую всех сил в этом случае можно пользоваться следующим алгоритмом:
При этом, обратите особое внимание на то, что:
Законы Ньютона
Законы динамики, описывающие влияние различных взаимодействий на движение тел, были в одной из своих простейших форм, впервые четко и ясно сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год), поэтому эти законы также называют Законами Ньютона. Ньютоновская формулировка законов движения справедлива только в инерциальных системах отсчета (ИСО). ИСО – система отсчета, связанная с телом, движущимся по инерции (равномерно и прямолинейно).
Есть и другие ограничения на применимость законов Ньютона. Например, они дают точные результаты только до тех пор, пока применяются к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика).
Первый закон Ньютона (или закон инерции)
Формулировка: В ИСО, если на тело не действуют никакие силы или действие сил скомпенсировано (то есть равнодействующая сил равна нулю), то тело сохраняет состояние покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции. Итак, причиной изменения скорости движения тела целиком или его частей всегда является его взаимодействие с другими телами. Для количественного описания изменения движения тела под воздействием других тел необходимо ввести новую величину – массу тела.
Масса – это свойство тела, характеризующее его инертность (способность сохранять скорость постоянной). В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг). Масса тела – скалярная величина. Масса также является мерой количества вещества:
Второй закон Ньютона – основной закон динамики
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела и сила. Первая из этих величин – масса – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила – является количественной мерой действия одного тела на другое.
Формулировка: Ускорение, приобретаемое телом в ИСО, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе этого тела:
Однако при решении задач по динамике второй закон Ньютона целесообразно записывать в виде:
Если на тело одновременно действуют несколько сил, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил. Если равнодействующая сила равна нолю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения, т.к. ускорение будет нулевым (первый закон Ньютона).
Третий закон Ньютона
Формулировка: В ИСО тела действуют друг на друга с силами, равными по модулю и противоположными по направлению, лежащими на одной прямой и имеющими одну физическую природу:
Эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга. Обратите внимание, что складывать можно только силы, которые одновременно действуют на одно из тел. При взаимодействии двух тел возникают силы, равные по величине и противоположные по направлению, но складывать их нельзя, т.к. приложены они к разным телам.
Алгоритм решения задач по динамике
Задачи по динамике решаются с помощью законов Ньютона. Рекомендуется следующий порядок действий:
1. Проанализировав условие задачи, установить, какие силы действуют и на какие тела;
2. Показать на рисунке все силы в виде векторов, то есть направленных отрезков, приложенных к телам, на которые они действуют;
3. Выбрать систему отсчета, при этом полезно одну координатную ось направить туда же, куда направлено ускорение рассматриваемого тела, а другую – перпендикулярно ускорению;
4. Записать II закон Ньютона в векторной форме:
5. Перейти к скалярной форме уравнения, то есть записать все его члены в том же порядке в проекциях на каждую из осей, без знаков векторов, но учитывая, что силы, направленные против выбранных осей будут иметь отрицательные проекции, и, таким образом, в левой части закона Ньютона они будут уже вычитаться, а не прибавляться. В результате получатся выражения вида:
6. Составить систему уравнений, дополнив уравнения, полученные в предыдущем пункте, в случае необходимости, кинематическими или другими простыми уравнениями;
7. Провести далее все необходимые математические этапы решения;
8. Если в движении участвует несколько тел, анализ сил и запись уравнений производится для каждого из них по отдельности. Если в задаче по динамике описывается несколько ситуаций, то подобный анализ производится для каждой ситуации.
При решении задач учитывайте также следующее: направление скорости тела и равнодействующей сил необязательно совпадают.
Сила упругости
Деформацией называют любое изменение формы или размеров тела. Упругими называют такие деформации, при которых тело полностью восстанавливает свою форму после прекращения действия деформирующей силы. Например, после того, как груз сняли с пружины, её длина в недеформированном состоянии не изменилась. При упругой деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Ее называют силой упругости. Простейшим видом деформации является деформация одностороннего растяжения или сжатия.
При малых деформациях модуль силы упругости пропорционален деформации тела. При этом сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации, и может быть рассчитана по формуле:
где: k – жесткость тела, х – величина растяжения (или сжатия, другими словами: деформации тела), она равна модулю разности между конечной и начальной длиной деформируемого тела. Важно, что величина растяжения или сжатия не равна ни начальной, ни конечной длине тела в отдельности. Жесткость не зависит ни от величины приложенной силы, ни от деформации тела, а определяется только материалом, из которого изготовлено тело, его формой и размерами. В системе СИ жесткость измеряется в Н/м.
Утверждение о пропорциональности силы упругости и деформации называют законом Гука. В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром.
Таким образом, у каждого конкретного тела (а не материала) есть своя жесткость и она не изменяется для данного тела. Таким образом, если у Вас в задаче по динамике несколько раз растягивали одну и ту же пружину Вы должны понимать, что ее жесткость во всех случаях была одна и та же. С другой стороны если в задаче было несколько пружин разных габаритов, но, например, все они были стальные, то тем не менее у них у всех будут разные жесткости. Так как жесткость не является характеристикой материала, то ее нельзя найти ни в каких таблицах. Жесткость каждого конкретного тела будет либо Вам дана в задаче по динамике, либо ее значение должно стать предметом некоторых дополнительных изысканий при решении данной задачи.
При сжатии сила упругости препятствует сжатию, а при растяжении – препятствует растяжению. Рассмотрим также то, как можно выразить жесткость нескольких пружин соединенных определённым образом. При параллельном соединении пружин общий коэффициент жесткости рассчитывается по формуле:
При последовательном соединении пружин общий коэффициент жесткости может быть найден из выражения:
Вес тела
Силу тяжести, с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни в неправильном смысле, под весом подразумевается масса, однако это не так.
Невесомость – это состояние, которое наступает, когда вес тела равен нолю. В этом состоянии тело не действует на опору, а опора на тело.
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Перегрузка рассчитывается по формуле:
где: P – вес тела, испытывающего перегрузку, P0 – вес этого же тела в состоянии покоя. Перегрузка – безразмерная величина. Это хорошо видно из формулы. Поэтому не верьте писателям-фантастам, которые в своих книгах измеряют ее в g.
Запомните, что вес никогда не изображается на рисунках. Он просто вычисляется по формулам. А на рисунках изображается сила натяжения нити либо сила реакции опоры, которые по третьему закону Ньютона численно равны весу, но направлены в другую сторону.
Итак, отметим еще раз три существенно важных момента в которых часто путаются:
Сила трения
Трение – один из видов взаимодействия тел. Оно возникает в области соприкосновения двух тел при их относительном движении или попытке вызвать такое движение. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней вызывающей силе и направлена в противоположную ей сторону. Сила трения покоя не может превышать некоторого максимального значения, которое определяется по формуле:
где: μ – безразмерная величина, называемая коэффициентом трения покоя, а N – сила реакции опоры.
Если внешняя сила больше максимального значения силы трения, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения. Силу трения скольжения можно считать равной максимальной силе трения покоя.
Коэффициент пропорциональности μ поэтому называют также коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Коэффициент трения положителен и меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки их поверхностей. Таким образом коэффициент трения является неким конкретным числом для каждой конкретной пары взаимодействующих тел. Вы не сможете найти его ни в каких таблицах. Для Вас он должен либо быть дан в задаче, либо Вы сами должны найти его в ходе решения из каких-либо формул.
Если в рамках решения задачи у Вас получается коэффициент трения больше единицы или отрицательный – Вы неправильно решаете эту задачу по динамике.
Если в условии задачи просят найти минимальную силу, под действием которой начинается движение, то ищут максимальную силу, под действием которой, движение ещё не начинается. Это позволяет приравнять ускорение тел к нулю, а значит значительно упростить решение задачи. При этом силу трения полагают равной ее максимальному значению. Таким образом рассматривается момент, при котором увеличение искомой силы на очень малую величину сразу вызовет движение.
Особенности решения задач по динамике с несколькими телами
Связанные тела
Алгоритм решения задач по динамике в которых рассматриваются несколько тел связанных нитями:
Движение тела по телу
В задачах этого типа важно учесть, что сила трения на поверхности соприкасающихся тел действует и на верхнее тело, и на нижнее тело, то есть силы трения возникают парами. При этом они направлены в разные стороны и имеют равную величину, определяемую весом верхнего тела. Если нижнее тело тоже движется, то необходимо учитывать, что на него также действует сила трения со стороны опоры.
Вращательное движение
При движении тела по окружности независимо от того, в какой плоскости происходит движение, тело будет двигаться с центростремительным ускорением, которое будет направлено к центру окружности, по которой движется тело. При этом понятие окружность не надо воспринимать буквально. Тело может проходить только дугу окружности (например, двигаться по мосту). Во всех задачах этого типа одна из осей обязательно выбирается по направлению центростремительного ускорения, т.е. к центру окружности (или дуги окружности). Вторую ось целесообразно направить перпендикулярно первой. В остальном алгоритм решения этих задач совпадает с решением остальных задач по динамике:
1. Выбрав оси, записать закон Ньютона в проекциях на каждую ось, для каждого из тел, участвующих в задаче, или для каждой из ситуаций, описываемых в задаче.
2. Если это необходимо, дополнить систему уравнений нужными уравнениями из других тем по физике. Особенно хорошо нужно помнить формулу для центростремительного ускорения:
3. Решить полученную систему уравнений математическими методами.
Так же есть ряд задач на вращение в вертикальной плоскости на стержне или нити. На первый взгляд может показаться, что такие задачи будут одинаковы. Это не так. Дело в том, что стержень может испытывать деформации как растяжения, так и сжатия. Нить же невозможно сжать, она сразу прогибается, а тело на ней просто проваливается.
Движение на нити. Так как нить только растягиваться, то при движении тела на нити в вертикальной плоскости в нити будет возникать только деформация растяжения и, как следствие, сила упругости, возникающая в нити, будет всегда направлена к центру окружности.
Движение тела на стержне. Стержень, в отличие от нити, может сжиматься. Поэтому в верхней точке траектории скорость тела, прикрепленного к стержню, может быть равна нулю, в отличии от нити, где скорость должна быть не меньше определенного значения, чтобы нить не сложилась. Силы упругости, возникающие в стержне, могут быть направлены как к центру окружности, так и в противоположную сторону.
Поворот машины. Если тело движется по твердой горизонтальной поверхности по окружности (например, автомобиль проходит поворот), то силой, которая удерживает тело на траектории, будет являться сила трения. При этом сила трения направлена в сторону поворота, а не против него (наиболее частая ошибка), она помогает машине поворачивать. Например, когда машина поворачивает направо, сила трения направлена в сторону поворота (направо).
Закон всемирного тяготения. Спутники
Все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними. Таким образом закон всемирного тяготения в виде формулы выглядит следующим образом:
Такая запись закона всемирного тяготения справедлива для материальных точек, шаров, сфер, для которых r измеряется между центрами. Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной. В системы СИ он равен:
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле или другой планете. Если M – масса планеты, Rп – ее радиус, то ускорение свободного падения у поверхности планеты:
Если же удалиться от поверхности Земли на некоторое расстояние h, то ускорение свободного падения на этой высоте станет равно (при помощи нехитрых преобразований можно также получить соотношение между ускорением свободного падения на поверхности планеты и ускорением свободного падения на некоторой высоте над поверхностью планеты):
Рассмотрим теперь вопрос об искусственных спутниках планет. Искусственные спутники движутся за пределами атмосферы (если таковая у планеты имеется), и на них действуют только силы тяготения со стороны планеты. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой орбите практически на нулевой высоте над планетой. Радиус орбиты таких спутников (расстояние между центром планеты и точкой где находится спутник) можно приближенно принять равным радиусу планеты Rп. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Скорость спутника на орбите вблизи поверхности (на нулевой высоте над поверхностью планеты) называют первой космической скоростью. Первая космическая скорость находится по формуле:
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу планеты. Для спутников, движущихся по круговым траекториям на значительном удалении от планеты, гравитационное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника в таком случае находится с помощью формулы:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Если речь идёт о планете Земля, то нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.