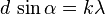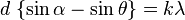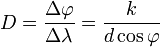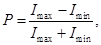Что такое дифракция френеля
Что такое дифракция френеля
Определить понятие зоны Френеля можно для дифракции на отверстии любой формы и даже вообще без отверстия, но практически полезно рассмотрение зон Френеля только при дифракции на круглом отверстии, причем в случае, когда источник света и точка наблюдения находятся на прямой, перпендикулярной к плоскости экрана с отверстием и проходящей через центр отверстия.
Если оба расстояния и гораздо больше диаметра отверстия, а обычно рассматривают именно такой случай, то из геометрических соображений (рис. 36) можно получить
Картина построения на комплексной плоскости совершенно аналогична картине для дифракции Фраунгофера на одной щели.
Рассмотрим теперь, как изменяется картина сложения комплексных амплитуд при изменении радиуса отверстия и сохранении остальных параметров задачи.
Если отверстие открывает две зоны Френеля, то картина сложения амплитуд будет иметь вид окружности. В этом случае суммарная амплитуда света в точке равна нулю (нулевая длина хорды).
Если открыто три зоны Френеля, то картина представляет собой полторы окружности, и так далее.
Для четного числа зон Френеля амплитуда в точке наблюдения равна нулю. Для нечетного числа амплитуда одинаковая, максимальная и равна длине диаметра окружности на комплексной плоскости сложения амплитуд.
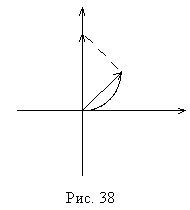
Иногда в задачах говорится, что какое-то (дробное) число зон закрыто, затем сколько-то зон открыто и остальные закрыты. Тогда суммарную амплитуду поля можно найти, как векторную разность амплитуд двух задач.
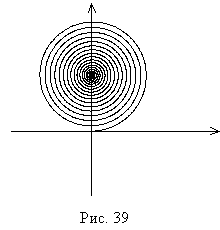
Центр спирали находится в середине окружности из первых двух зон, поэтому амплитуда поля при всех открытых зонах вдвое меньше, чем амплитуда поля при открытой одной первой зоне, а интенсивности различаются в четыре раза. Интенсивность света при открытой первой зоне Френеля в четыре раза больше интенсивности света перед экраном с отверстием.
Дифракция Фраунгофера.
Дифракция Френеля.
Сравнение линзы и зонной пластинки.
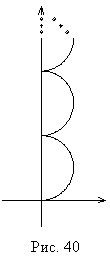
Препятствие на пути световой волны, в котором открыты только четные или только нечетные зоны Френеля, называется зонной пластинкой. Интенсивность света в точке наблюдения за зонной пластинкой многократно превышает интенсивность света, падающего на зонную пластинку. Причина этого в том, что свет от каждой открытой зоны Френеля приходит в точку наблюдения в одной и той же фазе. Ситуация похожа на фокусировку света линзой.
Линза в отличии от зонной пластинки никакие зоны Френеля не закрывает, она сдвигает по фазе на свет от тех зон, которые закрывает зонная пластинка. За счет этого амплитуда света удваивается. Кроме того линза устраняет взаимные фазовые сдвиги световых волн, проходящих внутри одной зоны Френеля. Она разворачивает пол окружности на комплексной плоскости для каждой зоны Френеля в отрезок прямой линии. За счет этого амплитуда возрастает еще в раз. В результате всю спираль сложения комплексных амплитуд на комплексной плоскости линза разворачивает в прямую линию.
Как линза выравнивает фазы дифрагированных волн? Линза выравнивает оптическую длину пути различных лучей, от источника до изображения. Это, в свою очередь, возможно потому, что оптическая длина пути в стекле в раз больше геометрической длины.
Получение изображения точечного источника с помощью линзы можно рассматривать или по правилам геометрической оптики, или как результат дифракции и интерференции волн, проходящих через различные участки линзы. В последнем случае большая интенсивность света в точке изображения получается, как результат интерференции волн, прошедших через разные участки линзы и пришедших в точку изображения в одинаковой фазе. В другие точки за линзой свет приходит через различные участки линзы в различных фазах, поэтому интенсивность света в других точках намного меньше, чем в точке изображения.
Дифракционный предел разрешения.
Более строгая теория для некогерентного освещения объекта дает выражение
Величину называют числовой апертурой.
Явление дифракции также ограничивает спектральное разрешение спектрометра. Вспомните нормальную ширину щели.
VII. ЗАКЛЮЧЕНИЕ.
В заключении сделаем несколько замечаний о полезности применения соображений размерности.
Многие соотношения в оптике, как и вообще в физике, могут быть получены путем построения простейшей зависимости требуемых величин с учетом необходимой размерности результата.
Подробнее смотрите литературу [2, 3].
VIII. ЛИТЕРАТУРА.
2. Бутиков Е.И. Оптика: Учеб. пособие для вузов/ Под ред. Н.И. Калитеевского.- М.: Высш. шк., 1986. 512с.
3. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720с.
Что такое дифракция френеля
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.
Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).
Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.
Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Что такое дифракция френеля
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.
Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).
Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.
Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Дифракция на круглом отверстии и диске.



Дифракция – огибание светом препятствия, проникновение света в область геометрической тени.
Принцип Гюйгенса—Френеля: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля 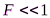
Суть метода такова. Пусть от светящейся точки 
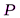
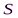
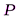
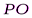
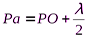
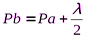
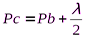


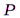
Дифракция Френеля на круглом отверстии:
С 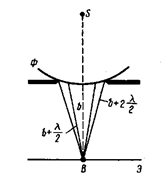
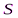
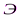
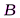
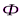
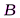
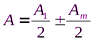

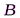
Дифракция Френеля на диске:
Сферическая волна, распространяющаяся из точечного источника 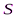
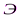
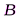
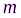
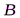
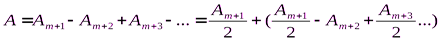
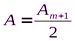
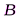
44) Дифракционная решетка
Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если известно число штрихов ( 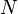
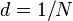
Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
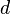
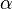
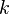
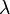
Если же свет падает на решётку под углом 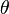
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом φ для длины волны λ и под углом φ+Δφ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δφ/Δλ. Выражение для D можно получить если продифференцировать формулу дифракционной решётки
Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра k.
45) Дисперсия света
Диспе?рсия све?та (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютономоколо 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.
Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно, чем больше частота световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде:
Однако в некоторых веществах (например в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет.
Дисперсия света позволила впервые вполне убедительно показать составную природу белого света.
По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу.
Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая).
Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов.
Огюстен Коши предложил эмпирическую формулу для аппроксимации зависимости показателя преломления среды от длины волны:
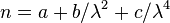
где 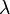
46) Поляризация света. Закон Малюса.
Испускание кванта света происходит в результате перехода электрона из возбужденного состояния в основное. Электромагнитная волна, испускаемая в результате этого перехода, является поперечной, то есть вектора 
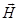



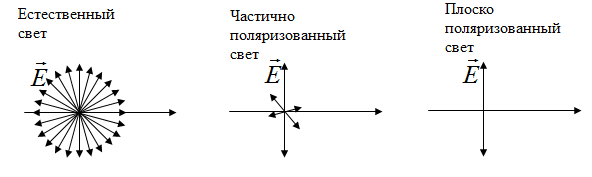
Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волна независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равновероятными колебаниями светового вектора 



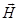
Вектор 
Степенью поляризации называется величина
где Imax и Imin – максимальная и минимальная компоненты интенсивности света, соответствующие двум взаимно перпендикулярным компонентам вектора