Что такое диаграмма состояния
диаграмма состояния
Полезное
Смотреть что такое «диаграмма состояния» в других словарях:
ДИАГРАММА СОСТОЯНИЯ — [phase equilibrium diagram) графическое изображение фазовых равновесий при разных значениях термодинамических параметров: температуры, давления и концентраций компонентов в фазах. В случае систем, не содержащих газовую фазу, слабым влиянием… … Металлургический словарь
ДИАГРАММА СОСТОЯНИЯ — диаграмма равновесия, фазовая диаграмма, графич. изображение равновесных состояний (см. Равновесие термодинамическое) в ва в виде точек в n мерном пространстве, по осям координат к рого отложены п независимых параметров состояния рассматриваемой… … Большой энциклопедический политехнический словарь
ДИАГРАММА СОСТОЯНИЯ — (фазовая Диаграмма) графическое изображение соотношения между параметрами состояния термодинамически равновесной системы (температурой, давлением, составом и др.). Диаграмма состояния позволяет определить, сколько и каких конкретно фаз образуют… … Большой Энциклопедический словарь
ДИАГРАММА СОСТОЯНИЯ — (диаграмма равновесия, фазовая диаграмма), геом. изображение равновесных состояний термодинамич. системы при разных значениях параметров, определяющих эти состояния: темп ры Т, давления р, состава системы (концентраций компонентов xi), мольного… … Физическая энциклопедия
Диаграмма состояния — диаграмма равновесия, фазовая диаграмма, графическое изображение соотношений между параметрами состояния физико химической системы (температурой, давлением и др.) и её составом. В простейшем случае, когда система состоит только из одного… … Большая советская энциклопедия
ДИАГРАММА СОСТОЯНИЯ — (фазовая диаграмма) графическое изображение равновесных состояний вещества в виде точек в n мерном пространстве, по осям координат которого отложены n независимых параметров состояния (объём, давление, температура, (см.), концентрации веществ и… … Большая политехническая энциклопедия
Диаграмма состояния — (фазовая) – графическое изображение всех возможных фазовых состояний термодинамической системы в пространстве основных параметров состояния – температуры, давления, объема или состава для многокомпонентных систем. [Ушеров Маршак А. В … Энциклопедия терминов, определений и пояснений строительных материалов
диаграмма состояния — Геометрическое изображение фазовых равновесий при разных значениях термодинамич. параметров: темп ры, давления и концентраций компонентов в фазах. В случае систем, не содержащих газ. фазу, слабым влиянием давления на фазовые равновесия обычно… … Справочник технического переводчика
диаграмма состояния — [phase equilibrium diagram] геометрическое изображение фазовых равновесий при разных значениях термодинамических параметров: температуры, давления и концентраций компонентов в фазах. В случае систем, не содержащих газовую фазу, слабым влиянием… … Энциклопедический словарь по металлургии
ДИАГРАММА СОСТОЯНИЯ — (фазовая диаграмма), графич. изображение всех возможных состояний термодинамич. системы в пространстве осн. параметров состояния т ры Т, давления ри состава х(обычно выражаемого молярными или массовыми долями компонентов). Для сложных систем,… … Химическая энциклопедия
State & Transition Diagram — что это и как применять
State & Transition Diagram (сокращенно S&T) — схема состояний и переходов. Техника для визуализации ТЗ. Она наглядно показывает, как некий объект переходит из одного состояния в другое.
Вот объект находился в состоянии А, потом произошло какое-то действие, и он попал в состояние В. Потом он попадет в состояние С и другие. Принцип не меняется, было одно состояние, стало другое.
кружочки — состояния объекта;
стрелочки — то, благодаря чему из состояния А в состояние В. Это действие, но его может совершить не только пользователь, но и система сама. Например, задача запустилась автоматически в 10 часов вечера.
Такая схема позволяет нам сразу визуально оценить, какие переходы вообще возможны и что надо протестировать. Ведь нам надо протестировать и эту стрелку, и эту. Так что стрелочки — это наши готовые тест-кейсы!
Схема состояний и переходов относится к техникам тест-дизайна. Значит, про неё спрашивают на собеседованиях. И поэтому я сделаю небольшой цикл статей по таким техникам в помощь начинающим тестировщикам. Чтобы ознакомиться с каждой техникой:
State & Transition Diagram (схема состояний и переходов) — текущая статья
Сегодня поговорим про State & Transition Diagram:
Как рисовать диаграмму
Очень важно: S&T рисуется на объект! Один объект. В идеале — на объект, имеющий аналог в базе данных продукта.
Шаг 1. Вы выбираете объект в своём проекте (рабочем или учебном, не суть).
Шаг 2. Думаете, какие у него состояния. Они не должны пересекаться, то есть: объект не может быть разом в двух состояниях, и при этом он всегда хоть в каком-то одном есть
Шаг 3. Рисуете эти состояния кружочками.
Шаг 5. Смотрите, что получилось и анализируете, есть ли у объекта другие состояния? А другие действия между текущими состояниями? Переход на шаг 2.
Кто не будет выполнять эту последовательность шагов, очень рискует вместо S&T нарисовать схему вышивки крестиком)))
Чтобы начать, задайте себе вопросы:
Какой конкретно объект вы выбрали? Как он называется? (только один!)
Какие у этого объекта есть состояния?
Основное определение состояния — «набор доступных и недоступных действий с объектом». Продукт всегда должен знать, в каком состоянии каждый его объект. Вообще, когда будете думать об объектах и состояниях, старайтесь представлять их аппаратную реализацию.
Объект — это практически всегда строка в базе данных, старайтесь абстрагироваться от интерфейса вообще, и представляйте те действия, которые вы могли бы делать с объектом прямыми запросами в базу.
Вот пример хорошей диаграммы:
State Transition на примере тортика!
В чатике моей школы для тестировщиков был очень интересный диалог по поводу рисования State Transition. Студентка рисует его для просмотра сериала и пытается разобраться, как это сделать:
— В ДЗ получила фидбэк, что сделала не схему состояний и переходов, а некую инструкцию по просмотру сериала, по факту показывающую одно его состояние — в процессе просмотра. Но суть как раз в том, что сериал из непросмотренного может быть перемещен в другие состояния, отраженные в виде разделов в личном кабинете, с помощью четырех кнопок, которые на схеме являются действиями. Больше никаких действий с сериалом пользователю не доступно (загрузка, редактирование и т.д.)
— Ну смотрите, Вы продолжаете описывать и смотреть на вещи, как пользователь, а надо как тестировщик. Сериалы из пустоты не берутся. Кто-то их закачивает. Значит, все же связка «сериала не существует» и «сериал загружен на сайт» — уже есть)
— Да, конечно, есть, но выполнять ее может очень ограниченный круг лиц, и я в процессе тестирования не могу. (студенты выбирают любой общедоступный проект и тестируют его. Разумеется, доступа в админку у них нет)
— По-хорошему у тестировщиков на это есть права) и им дают необходимый доступ.
— То есть важны состояния только по отношению к сайту, а что там с этим сериалом происходит в аккаунте уже считается как одно — просмотр? Тестировщик я без году неделя, а пользователь — много лет 🙂 Поэтому и прошу постановки мозгов.
Тут моя коллега решила объяснить рисование карты на примере. Тортика! Дальнейший диалог был просто потрясающий, не могу не поделиться им с вами (разумеется, с разрешения коллеги, все же это ее идея, а не моя). Итак, приступаем:
— Вот смотрите. Торт любите? Или другую еду какую-нибудь)
Чтобы приготовить торт, нам нужны ингредиенты, правильно? Это то, из чего он состоит. Как и наши объекты из параметров, но только в граммах.
Так вот, от того, что какого-то ингредиента будет больше/меньше, состояние торта не изменится. Он будет по-прежнему «не существует».
Чтобы его состояние изменилось — надо начать что-то с ними делать. Например, смешать, залить в форму и отправить в духовку. Тогда состояние будет «В процессе готовки».
Потом, когда бисквит испечется, мажем его кремом и украшаем. Он становится у нас «Торт украшен».
Но сразу есть его нельзя, мы ставим в холодильник, чтобы украшение застыло, а только потом мы можем его есть. После холодильника состояние становится «Торт готов». А вот дальше — разнообразие)
Мы можем съесть торт, тогда он станет «Торт съеден».
Возможно, мы уедем и не съедим торт, пока его можно есть. Тогда он станет «Торт испорчен».
Кстати, в процессе приготовления могли быть и другие ответвления. Например:
— передержали бы бисквит, состояние изменилось бы на «Торт испорчен»;
— не стали бы украшать бисквит и корж испортился бы → «Торт испорчен»;
— Ну тут-то я, получается, покупаю готовый торт. И уже размышляю, что с ним делать.
— Ок, изначально торта у Вас не было. Потом у Вас появилось состояние «Торт куплен». А дальше то, что происходит после «Торт готов» ¯\_(ツ)_/¯
Торт может быть съеден, может стать испорченным, может быть подарен, а только потом его уже съедят/не съедят, может быть выброшен. Все зависит от системы.
— То есть, я правильно понимаю?
2. Поставила в холодильник на потом
3. Передумала, достала, надкусала
4. Снова передумала, решила съесть целиком, осилила половину
5. Расстроилась и решила не доедать вообще и выкинуть
Это всё не важно и состояние торта не меняется, пока он не съеден или не стух?)
— Ну он же еще является тортом? Если его начали есть, но не закончили — можно ввести промежуточное состояние «В процессе уничтожения» =))
1-2 это торт куплен
3-4 это в процессе уничтожения
— Тогда чем это отличается от
1. Купила — добавлен на сайт/загружен на сайт/находится на сайте
2. Поставила в холодильник на потом — сохранен, чтобы посмотреть позже
5. Расстроилась и решила не доедать вообще и выкинуть — просмотр прерван/торт в помойке
— 5-е он еще в процессе.
У сериалов обычно прогресс есть, и его просто так не убрать 🙂
— либо он в процессе просмотра
Примеры S&T
Примеры диаграмм можно посмотреть в конфлюенсе (доступ открытый без авторизации). Туда я выношу хорошие работы своих студентов. Их там сильно больше, чем в этом разделе статьи + обычно там можно и сам исходник скачать, чтобы внимательно всё рассмотреть. Welcome =)
Вот некоторые из этих работ:
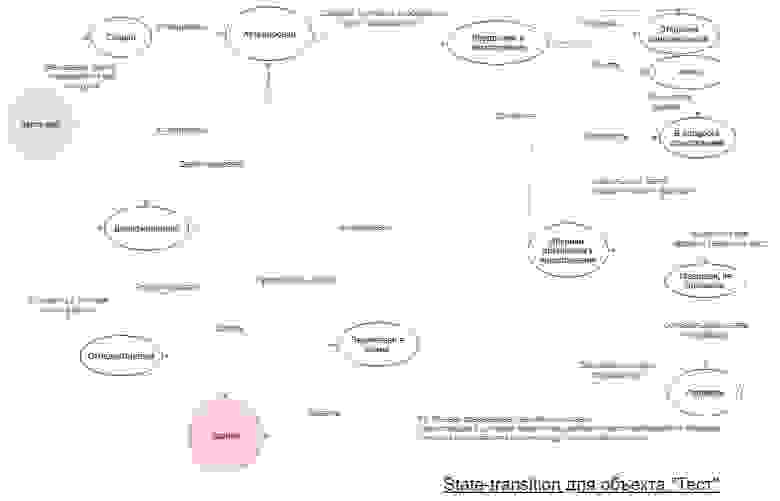
Ольга (объект — тест)
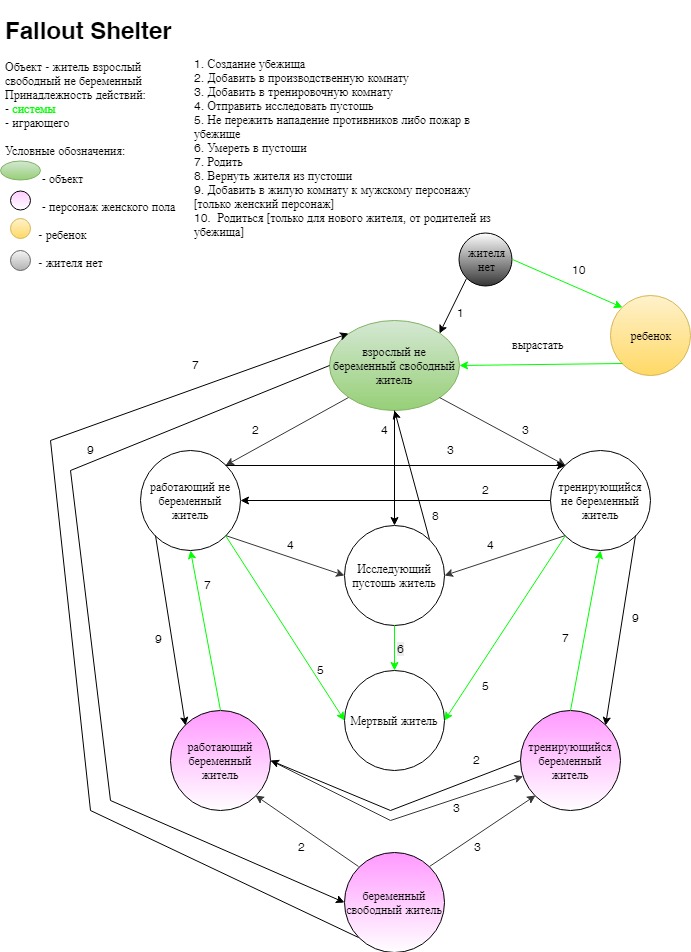
Кристина (Fallout Shelter)
Fallout Shelter — игра под iOS, Android. В постапокалиптическом мире несколько людей было выбрано для создания светлого будущего. Их поместили в небольшое убежище, уходящее под землю. Это убежище необходимо развивать, защищать от угроз из внешнего мира, увеличивать количество жителей, производить ресурсы, выполнять квесты.
State Transition для пина в Pinterest
Типовые ошибки при составлении карты
На примере своих студентов мы собрали несколько типовых ошибок, которые допускают тестировщики, впервые рисуя карту:
1. Вместо объекта — GUI
Очень важно: S&T рисуется на объект! Это не зарисовка графического интерфейса «открыта страница такая, открыта страница сякая». Если вы описываете разные странички GUI — это уже не S&T.
Зарисовывать страницы смысла обычно нет. Это как при рисовании майнд-карты — мы не рисуем графический интерфейс, мы описываем функционал. То, зачем пользователь вообще пришел на сайт. Это намного полезнее!
Другой вариант той же ошибки: искать билет — (результаты поиска) — открыть форму покупки — (форма открыта) — ввести данные кредитной карты — (данные введены).
2. Несколько объектов в одной карте
На прошлой картинке у нас несколько объектов: результаты поиска, форма, данные. И все — плохие. Потому что там мы явно что-то покупаем, вот это «что-то» и есть объект!
Но когда мы описываем покупку, тоже легко скатиться в несколько объектов в одной карте: «пицца в корзине», «заказ оформлен».
Товар тоже очень часто путают, потому что есть два варианта:
как на авито — продается конкретная вещь: «Нет на сайте», «Продается», «Продан».
просто «товарная позиция», как какие-нибудь носки в магазине одежды: «Отсутствует», «В наличии», «Ожидается поступление» и так далее.
Если речь о сайте типа авито, то объект лучше выбрать «объявление», будет логичнее. А вот если мы покупаем пиццу — это будет товарной позицией.
3. Несколько одинаковых состояний
Вспомните пример с тортиком:
Поставила в холодильник на потом.
Передумала, достала, надкусала.
Снова передумала, решила съесть целиком, осилила половину.
Расстроилась, решила не доедать вообще и выкинуть.
Половину пунктов можно объединить. Ведь состояние торта не меняется от того, купили вы его только что или час назад, сидите любуетесь на него, переставляете с места на место или убираете в холодильник:
1-2 это торт куплен;
3-4 в процессе уничтожения;
Другой пример — объект «пин»:
пин перенесен другим пользователем себе на доску.
Но, когда пин откомментирован или сдублирован — это тоже самое, когда он просто создан. Состояние самого пина не меняется!
товар найден при поиске
Одно и то же с точки зрения товара. Он как был, так и есть.
Плюсы подхода
Плюс рисования — это визуализация ТЗ, которая:
Позволяет увидеть, что мы упустили
На входе унылая стена текста, а мы красиво зарисовали, при этом разными цветами — вот данные попали туда, вот сюда. В итоге наглядно видим весь маршрут нашего объекта.
И пока мы рисуем его маршрут, мы можем сразу же заметить, что «Ага! Вот из этого состояния, наверное, можно вернуться ещё вот в это», то есть мы можем понять, что упускаем. А если бы не нарисовали, то даже не додумались бы до такого теста!
Минусы подхода
Не всегда визуализация делает ТЗ понятнее. И тогда начинаем думать, как это решать:
Слишком насыщенная карта — разбиваем на несколько маленьких.
Сложно поддерживать — нужна ли она вообще?
Если на диаграмме куча всего — это плохо, ведь ее главная фишка — понятность. И если мы на нее смотрим и просто теряемся в этом объеме стрелочек — значит, схема нам не помогает.
Поэтому если схема насыщенная — разбиваем на мелкие. Которые, возможно, ссылаются друг на друга. То есть вот есть верхнеуровневая схема, а вот на каждое действие есть уровни подетализированнее.
Не стоит рисовать все-все-все стрелочки. Из любого состояния можно закрыть браузер, но не надо рисовать это. Просто держите в уме, что есть кнопка «закрыть», а еще может интернет пропасть, или сервер упадет, или еще какая катастрофа случится.
На диаграмме же показываем все важные стрелочки. Если их слишком много, то придумываем, как уменьшить их количество, чтобы не переборщить, потеряв наглядность.
Инструменты для рисования
Xmind (freemind, etc)
Основной инструмент — ручка и бумага, или маркер и доска. Потому что если вам надо просто обсудить, что будет, «если из этого состояния перейти в это, и как должна система реагировать, если происходит вот то», то вполне достаточно нарисовать это от руки.
К тому же от руки получается быстрее, а иногда еще и красивее. Почему? Потому что когда мы начинаем использовать инструмент, то он нас ограничивает. Вот, нам надо нарисовать стрелочку, так, а как нам это сделать. Мы начинаем думать в стиле инструмента. Это как когда мы создаем презентации в power point, то вместо мыслей о докладе думаем, как бы назвать новый слайд.
А если бумажка рядом, можно спокойно генерить в голове идеи и условия. Что придумал? Зарисовал кое-как. Если очень хочется, потом перерисовал красиво. А, может, и так сойдет.
В любом случае смотрите сами. Если удобен какой-то инструмент — используйте его! Хорошо получаются такие схемы в Xmind или Yed, или в гуглодокументах. Попробуйте использовать несколько разных инструментов, а потом выберите тот, что больше по душе. Но в целом бумага и ручка вполне себе вариант!
Итого
Рисунок — мощнейший инструмент визуализации. Вот вы открываете статью с картинками, типа этой. На что вы смотрите в первую очередь — на картинку или на текст? Правильно, на картинку.
Поэтому я за то, что рисовать! Нарисовали? Добавили в ТЗ! Всем удобнее, даже заказчику. Ведь с картинками текс становится понятнее.
Настоятельно рекомендую рисовать диаграмму состояний и переходов. Пусть даже одноразово, маркером на доске, чтобы обсудить новое ТЗ, которое пришло от аналитиков.
Зарисовали, позвали аналитика и стали обсуждать:
— А вот смотрите, вот эта стрелочка. может нам стоит сделать еще вот это?
— А что будет, если вот так?
Кстати, лайфхак. Если зарисовали маркером и жалко свое творчество (уж больно продуктивное общение с командой вышло) — сфотографируйте и выложите в конфлюенс рисунок! Не обязательно тратить время на перерисовку =)
См также (напомню ссылочки):
Как составлять вариант использования — вариант оформления требований без рисований.
Проектирование диаграммы состояний UML (Statechart Diagram)
Программные решения для бизнеса
В данном занятии демонстрируется построение диаграммы состояний заявки клиента. Основные шаги построения диаграммы состояний:
Каждый переход имеет метку, состоящую из следующих необязательных частей:
Триггер-идентификатор — единственное событие, способное вызвать изменение состояния. Пропуск этой части означает, что переход происходит немедленно
Защита — логическое условие, выполнение которого обязательно для осуществления перехода. Пропуск защиты означает, что в ответ на инициирующее событие переход всегда осуществляется
Активность — поведение системы во время перехода. Пропуск активности означает, что в процессе перехода ничего не происходит
Внутренние активности (internal activities) используются для описания действий объекта, совершаемых без перехода. Список основных действий включает следующие значения:
Автоматное программирование. Часть 2. Диаграмма состояний и переходов
В первой статье я дал пример автоматного программирования от общего к частному, а точнее конструктивную декомпозицию. Следующий этап проектирования, проработка получившихся модулей. Но сначала я покажу чем являются автоматы с математической и практической точки зрения. В основе автоматов лежит модель описывающая процесс протекающий во времени, называемая диаграмма состояний, и невозможно себе представить автоматное программирование без этой сущности. Почему это так рассматривается в сегодняшней статье.
Автомат vs автомат
Специалисты приводят довольно разветвлённую классификацию автоматов: детерминированные и недетерминированные, конечные и бесконечные, Мили и Мура, синхронные и асинхронные, и т.д. Однако с точки зрения пользователя это всё равно, как если бы человек хотел решить для себя — нужен ли ему личный автомобиль в мегаполисе, а ему рассказывали бы о количестве цилиндров, и инжекторе.
Как популяризатор отмечу, что с точки зрения использования автоматы делятся на две связанные категории:
Рисунок 1. Автоматное проектирование и автоматная реализация
Насколько становится понятно из общения с коллегами, существует категория формалистов, людей рассматривающих автоматы как:
То, ради чего хочется использовать автоматы – простота и в то же время глубина проектирования. В предыдущей части было показано, что в основе автоматно-ориентированного проектирования модулей, лежит разбиение задачи на операционный автомат (ОА) и управляющий автомат (УА), причём операционный автомат в свою очередь может быть повторно разбит на операционный автомат нижнего уровня и его управляющий автомат.
Операционный автомат это полуфабрикат, который может оптимально выполнять некоторое действие, но при этом его «не волнует» когда выполнять это действие и с какими параметрами. Операционный автомат может делать это с любыми допустимыми параметрами. Отличный пример операционного автомата АЛУ.
В свою очередь, параметризация и запуск операционного автомата ложится на плечи управляющего автомата.Многоступенчатость разбиения позволяет избежать получения сложного управляющего автомата с не очевидной, хотя и железной логикой, заменив его несколькими простыми управляющими автоматами с максимально понятным функционированием.
Реализация управляющего автомата при этом может быть совсем не автоматной, или быть автоматной, но без таких атрибутов как: состояния закатанные в отдельные функции, таблицы сигналов и соответствующих им переходов. И, наконец, замечу, что любая программа является автоматом, и тем не менее не все программы являются автоматно реализованными.
Но в таком случае, что подразумевать под автоматно реализованной программой?
Реализация: автоматная vs не автоматная.
Главным атрибутом автоматно реализованной программы является:
Теперь есть чёткий критерий, по которому мы относим программы к автоматно реализованным программам, но кто-то спросит: в чём прикол автоматной реализации, почему в некоторых случаях она более ценна?
Главное, что отличает автоматно-реализованные алгоритмы от реализованных неавтоматно лежит в сфере нашей психики, а точнее того как мы мыслим. Как метко заметил коллега:
«Человеческий разум устроен так, что ему проще понимать алгоритмы, которым скармливают данные на входе и получают данные на выходе, и результат зависит только от входа, но не от внутреннего состояния. Такие «чистые функции» (назовём их аналитические прим.авт.) проще понимать, тестировать и использовать повторно».
Поведение аналитической функции можно представить в виде некоторой таблицы или графика: есть что-то на входе и есть однозначное соответствие на выходе. Однако цифровые устройства в большинстве таковы, что используя в качестве кирпичиков аналитические функции, в результате мы всё равно получаем программу, поведение которой зависит уже и от внутреннего состояния. То есть, использование аналитических функций не решает проблему «понимаемости», перемещая её на другой уровень!
Чтобы проиллюстрировать термин «понимаемость» и особенности человеческого мышления, предлагаю рассмотреть, как записывается один и тот же абстрактный алгоритм, реализованный автоматно и неавтоматно.
Рисунок 2. Обобщённый пример управляющего устройства (а) и граф-схема описывающая работу этого устройства (б).
Некая программа предназначена для управления неким устройством. Как показано на рис 2 а, непосредственно «железом» управляет не уточняемый ОА, которым управляет УА, алгоритм работы которого изображён на рис. 2 (б). УА обрабатывает внешние команды, условно обозначаемые набором символов <0,1,2>, и транслирует их в набор микроинструкций, управляющих операционным автоматом. Под микроинструкцией я подразумеваю нужный для получения эффекта набор команд. Каждый набор микроинструкций условно обозначен символом <1,2,3,4,5,6>. Флаги
Поскольку это цифровое устройство с памятью, описанный рис 2 алгоритм фактически является автоматом, несмотря на то, что реализация алгоритма неавтоматная. Это приводит к тому, что в нем нет явно выделенных состояний, в результате чего текущее состояние неявно определяется флагами. При этом описание программы граф-схемой само по себе не противоречит автоматному принципу, автоматно-реализованную программу можно описать граф-схемой, будет и такой пример. Основная загвоздка, связанная с граф-схемой — низкая понимаемость программы описанной ГС с точки зрения динамического, т.е. протекающего во времени процесса.
Вот, что я имею в виду: это очень простой пример, но здесь нельзя однозначно сказать, какой выходной сигнал будет соответствовать входному сигналу 0, потому что это будет зависеть от состояния флагов, а точнее флага b, которое в свою очередь зависит от того, что было на входе ранее. Точно также непросто с ходу сказать, какая выходная последовательность будет соответствовать входной последовательности: 2,1,0,2,1,0. Для этого нужно фактически выполнить алгоритм.
Для того чтобы дать полное соответствие входных и выходных сигналов, то есть описать функцию в виде таблицы, потребуется произвести тотальное тестирование, да ещё и к тому же результат получится в виде двухсигнальных последовательностей, в которых по очереди перебираются всевозможные входные комбинации.
Рисунок 3. Временная диаграмма – способ описания поведения систем с памятью.
Поскольку три бинарных флага позволяют отслеживать не более (но возможно и не менее) 8ми предшествовавших символов, то для алфавита из 3х входных символов, чтобы описать все возможные варианты нам потребуется привести 6561 диаграмм, так называемая мощность произведения множества входных сигналов и множества состояний, которая с ростом числа состояний и размера алфавита входных сигналов растёт геометрически.
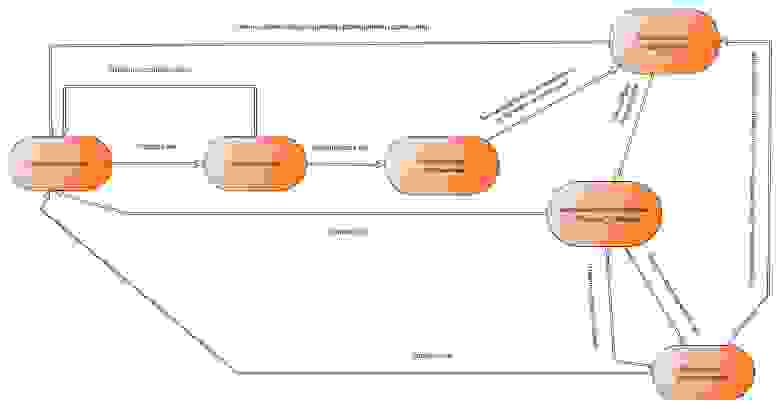
Автоматная реализация программы позволяет описать её при помощи диаграммы состояний, а диаграмма состояний и переходов даёт кардинально иной подход к анализу динамических систем с памятью. Построим автомат, который реализует изображённый на рис 2 б алгоритм (я не буду здесь уточнять как, это тема другого разговора), и который описывается диаграммой состояний и переходов изображённой на рис 4. Название состояния на диаграмме совпадает с выходным символом, когда автомат в этом состоянии.
Рисунок 4. Диаграмма состояний и переходов соответствующая изображённому на рис 2 алгоритму.
Пользоваться этой диаграммой очень удобно, поскольку на переходы влияют только входные символы, нет никаких дополнительных условий. Иными словами, чтобы анализировать реакцию на входной символ для реализации рис 2 нужно иметь перед глазами текущее состояние флагов, в каждой итерации новое, а для того чтобы анализировать поведение устройства реализованного как показано на рис 4, не нужно ничего кроме этой диаграммы.
Это важное преимущество автоматного подхода, называемое:
Взгляд на динамические процессы вне временной оси.
Человеческий мозг устроен так, что легче работать с таблицей цифр, чем если ту же таблицу показывать по одной цифре по очереди. В первом случае человек способен выявлять сложные закономерности, во втором едва ли сможет определить какую-либо закономерность, кроме простейших, даже если прокручивать таблицу циклически.
Рассмотрим пример, пусть у нас есть последовательность команд
Согласитесь, каждое из действий отличается простотой замысла. Однако, не выполнив всех действий нельзя сказать, что у нас получится. Результат выполнения этого алгоритма приведён, на рис. 5 а
а) б)
Рисунок 5. Результат выполнения последовательности команд (а), и результат выполнения этой же последовательности, если допущена ошибка(б).
В то же время, ошибись я в расчётах, и укажи, например, в первом операторе второй строки вместо (1,-3) значение (2,-3) результат работы был бы иной (5 б), но глядя на текст программы этого нельзя понять. И это простой случай, когда результат можно увидеть сразу после выполнения. Если бы мы видели результат в виде отдельно взятой линии в каждый момент времени, или имели дело не с графикой, а с цифрами, наша ошибка была бы не столь очевидна.
Это непростой для человеческого мозга вид информации, называемый динамический процесс, как последовательность действий (в примере отдельные линии), дающих в результате наложения некоторый предполагаемый результат (в примере рисунок).
Неплохим примером взгляда на динамические процессы вне временной оси является анализ сигналов в частотной области. Рассмотрим сигнал рис 6. В чём-то его можно сравнить с временной диаграммой автомата. Это тоже последовательность действий: сигнал пересёк 0, пошёл вверх, достиг максимума, пошёл вниз, снова пересёк 0.
Рисунок 6. График сигнала, аналог временной диаграммы для автоматов.
Очевидно, что это периодический сигнал, можно даже угадать, что он состоит из нескольких синусоид, но нам сложно сказать из каких.
В то же время спектр прямо даёт нам представление о структуре сигнала.
Рисунок 7. Спектр сигнала изображённого на рис 6.
Спектр можно сравнить с автоматной диаграммой вот в каком отношении: он содержит статическое описание того, что лежит в основе процесса, протекающего во времени. И спектр и диаграмма состояний и переходов дают возможность анализировать процесс вне временной оси, охватывая его в целом, а не как последовательность шагов.
Немного математики
Диаграмма состояний и переходов, как строгая математическая категория даёт возможность углублённого анализа.
Проанализируем описанный диаграммой состояний и переходов рис 5 процесс. Для этого нам потребуется понятие изоморфного автомата. Изоморфные автоматы — математический термин, означающий автоматы, которые фактически являются одним и тем же автоматом, с переименованными состояниями и/или сигналами.
Рисунок 8. Изоморфные автоматы.
Из условий задачи следует, что мы ничего не знаем о процессах, которые моделирует алгоритм рис. 2 б. Тем не менее, анализ приведённой на рис. 4 диаграммы позволяет выделить два очень похожих кластера, переключение между которыми производится в основном сигналом 0.
Построим автомат, изоморфный исходному, но у которого переименованы номера состояний как это показано на рис 9 и очертим на нём указанные кластеры. В кластере с состояниями 4,5,6 в скобках указаны идентичные состояния первого кластера.
Рисунок 9. Автомат, изоморфный изображённому на рис.4
Декомпозируем (разобьём) исходный автомат на два параллельных автомата, как показано на рис. 10.
Рисунок 10. Параллельная декомпозиция автомата показанного на рис 9.
Выходной символ каждого из автоматов приведён через слеш после названия состояния. Выходные символы полученных автоматов арифметически складываются, давая на выходе символы от 1 до 6, полностью соответствующие символам на выходе исходного автомата при таких же входных данных. Такое соединение автоматов называется параллельная композиция.
Обратите внимание на Автомат 2. В каком бы состоянии он не находился, входной символ 0, приводит к появлению на выходе символа 1, входной символ 1 к появлению на выходе символа 3, а символ 2 к появлению символа 2. То есть, фактически это комбинационная схема, массив выходных символов, а индекс массива — символ на входе. Изобразим автомат как это показано на рис. 11
Рисунок 11. Автомат эквивалентный автомату изображённому на рис. 10
Поскольку выходные символы у нас кодировали некий набор микроинструкций, может показаться, что арифметические преобразования здесь неуместны, однако, если посмотреть на проблему глазами математика и представить, что у нас есть массив реализованных микроинструкций, в котором каждая микроинструкция имеет индекс, в этом случае корректность произведённых нами преобразований не вызывает сомнений.
Подчеркну особо, поскольку символы 0,1,2 на входе и символы 1,2,3 на выходе относятся к разным алфавитам, то нельзя просто так взять и подать символ 1 с выхода обратно на вход. Однако, могут быть такие автоматы, в которых входной и выходной символы принадлежат одному алфавиту и в этом случае выходные символы автомата можно подавать на его вход. Это называется композиция с обратной связью. Таким композициям посвящён параграф 4.7 лекций.
Из условия задачи не была известна природа объекта, который моделируется алгоритмом
рис. 2 б, и тем не менее, анализируя и декомпозируя автоматы, мы установили что в основе моделируемого явления лежат на самом деле два независимых процесса, которые вносят свой вклад в конечный результат. И хотя в случае абстрактного примера это не даёт ничего, кроме интересного наблюдения, в случае конкретной задачи приведённый анализ может раскрыть неочевидные аспекты моделируемого явления, поэтому он интересен не только с точки зрения программирования, но и с инженерной точки зрения. Для инженера понимание процессов лежащих в основе явления может скорректировать взгляд на разрабатываемое устройство и получить оригинальное, бьющее в самую суть техническое решение.
Рассмотренный пример затрагивает ещё одно важное и полезное свойство автоматов, понятие эквивалентных автоматов. Дело в том, что может существовать сколь угодно много автоматов, с разным количеством состояний (т.е. речь идёт не об изоморфных автоматах), которые на одну и ту же входную последовательность дадут одинаковый отклик. Соответственно, если поместить их в «чёрный ящик», то нельзя будет отличить их, подавая на вход разные последовательности и анализируя отклик.
Одни автоматы при этом будут более «расточительны» с точки зрения количества внутренних состояний, другие более «экономны». Среди всего множества эквивалентных автоматов будет автомат с минимально возможным количеством состояний, и он называется минимальный автомат. Более того, существуют алгоритмические методики получения из любого автомата эквивалентного ему минимального. Это свойство в частности означает, что при составлении диаграммы состояний и переходов не следует гнаться за минимизацией числа состояний, но следует добиться максимально ясной и полной картины. И хотя часто понимаемость и простота реализации связаны, может оказаться, что нагляднее представить результат в виде пары автоматов как в нашем примере. После этого, при помощи математических алгоритмов можно найти эквивалентный минимальный автомат.
Поскольку у меня нет замысла рассматривать в этой статье теорию автоматов, перечислю вкратце основные математические операции, которые можно выполнять над автоматами: композиция, декомпозиция, минимизация, получение автомата из микропрограммы, получение микропрограммы на основе автомата, алгебраические операции над автоматами (сложение, сравнение автоматов), построение имитирующего автомата и пр. Теоретические обоснования и методики выполнения данных преобразований можно найти, например здесь.
В случае автоматной реализации состояние — математическая категория. В каждый момент времени оно однозначно определено, в частности программным счётчиком. Мы сами задаём тот набор состояний, который нужен для решения задачи управления и для каждого состояния явно выбираем исходя из потребностей какое состояние будет следующим, если придёт команда Х или Y. Если не хватает состояний, можно произвольно увеличивать их количество до требуемого, однозначно прописывая связи между ними.
Я хочу, чтоб меня поняли верно. Реализуя программу автоматно, вы тоже не застрахованы от опечаток или неверного замысла. Неправильно смоделировав устройство, можно задать переход не в то состояние, но это уже не ошибка проектирования ПО, а инженерная ошибка, т.е. это не связано с тем какой путь — автоматный или неавтоматный выбран. При неавтоматной реализации к тем же самым ошибкам моделирования и опечаткам добавляется мощный источник потенциальных логических ошибок название которому: динамический процесс как последовательность действий, дающих в результате наложения некоторый предполагаемый результат.
В следующей части мы вернёмся на твёрдую почву практических алгоритмов, устроив соревнования между двумя реализациями примера «Дисплей», одна из которых разработана автоматно, а другая нет, а так же рассмотрим итерационный процесс на примере модификации автомата для примера «Дисплей».
Список рекомендованной литературы. Если есть потрясающий сюжет про автоматы, пишите мне, я добавлю.