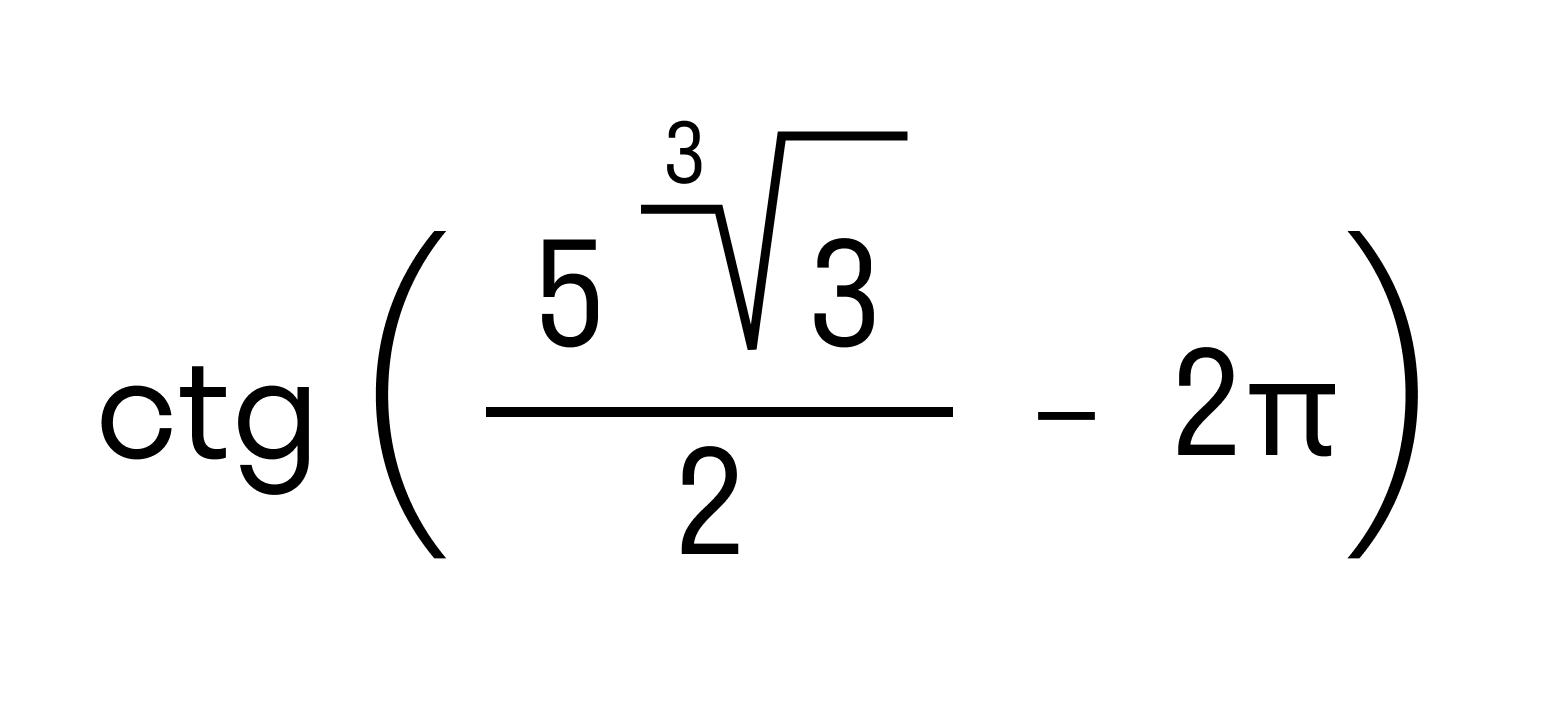Что такое действительные числа в алгебре

Общие сведения

Результатом математических операций (деления, произведения, сложения, вычитания, возведением в степень и т. д. ) могут быть действительные числа. Примерами являются любые значения. Действительное число — совокупность рациональных и иррациональных величин. Международное обозначение — литера «R».

Следует отметить, что рациональные величины представляются в виде десятичной (конечной) или бесконечной периодической десятичной дроби. В первом случае число имеет определенное количество знаков после запятой, результат которого получен при делении двух значений. Например, 8/5 = 1,6. Последняя величина ограничена десятыми долями.

Бесконечная десятичная периодическая дробь представляет собой вещественную величину с бесконечным количеством знаков после запятой. Например, при делении 5 на 3 получается результат, равный 1,(6). Запись читается таким образом: одна целая и 6 в периоде.

В случае иррациональных чисел — бесконечные непериодические дроби, т. е. после запятой идет бесконечная запись, которая не повторяется вообще. Например, 1,213456789523648 и так до бесконечности.

На основании этой информации можно получить другое определение: действительные — это числа, которые можно записать в виде конечной или бесконечной десятичной дроби. Кроме того, нуль принадлежит также множеству R. Он является единственным значением, которое не является положительным и отрицательным. В некоторых источниках можно также встретить другое название действительных чисел — вещественные.

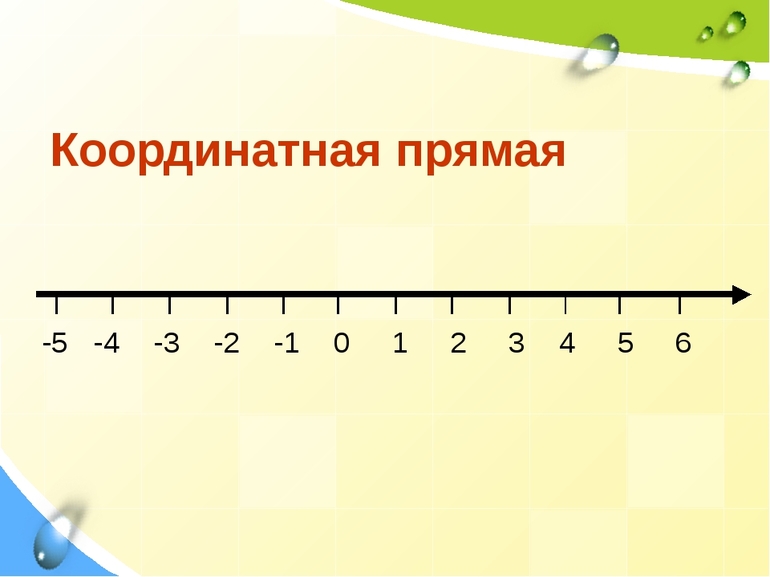
Координатная прямая

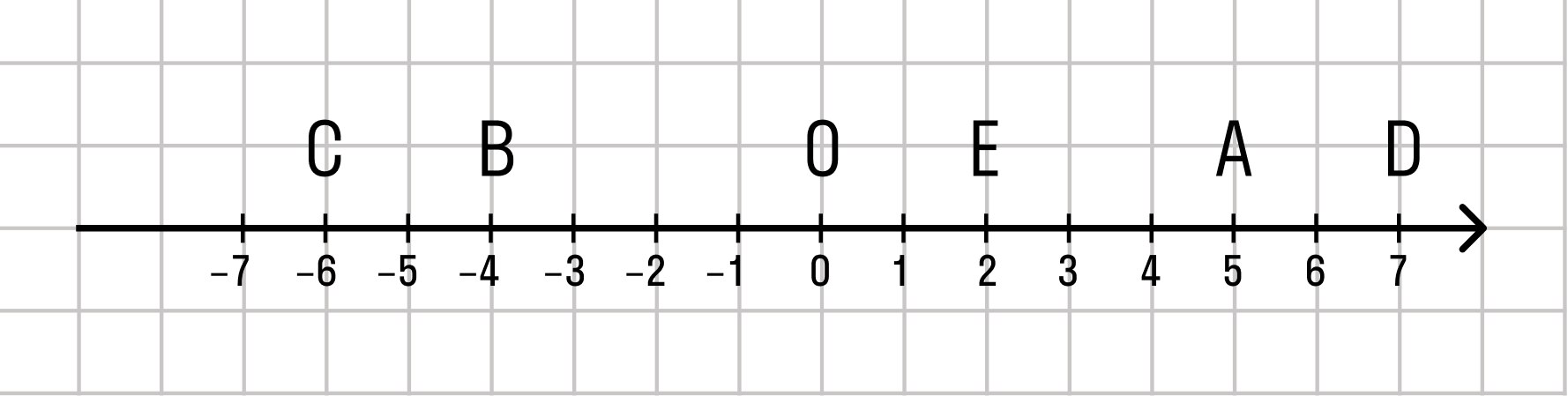
Для представления положения любого R применяется координатная прямая, являющаяся их геометрическим смыслом. Величины на ней отмечаются в порядке возрастания. Перед построением следует начертить произвольную прямую, а затем отметить на ней точку 0 (нулевую отметку). После этого можно приступить к откладыванию числовых значений. Слева от нулевой координаты расположены отрицательные, а справа — положительные числа.

Из курса геометрии 5 класса можно вспомнить следующее определение: прямой называется произвольное геометрическое место точек, расположенных в один ряд до бесконечности. Иными словами, прямая — линия, не имеющая начала и конца, т. е. она не ограничена в пространстве.

Координатную прямую используют при решении дифференциальных уравнений, неравенств, поиска области значения функции и т. д.

Представление действительных чисел

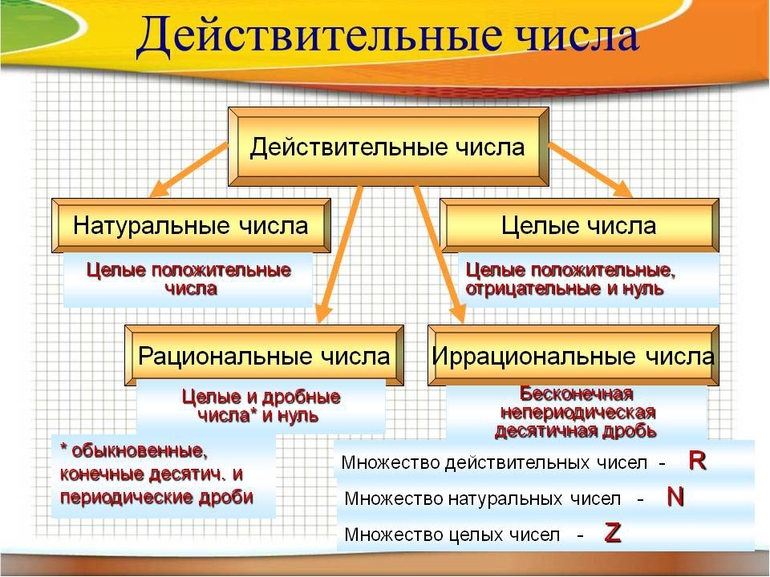
Для представления действительных чисел следует разобрать значения, которые к ним относятся. Эта классификация рекомендована математиками. Она имеет такой вид:

К первой группе относятся числа, которые изобрели древние греки. Их еще называют природными. Они применяются при сложных вычислениях на рынках, магазинах и других разнообразных расчетах. Во вторую категорию входят все целые (положительные и отрицательные) и 0. Дробные состоят из десятичных и обыкновенных дробей. К первым относятся значения, состоящие из целой и дробной частей. Последние отделяются посредством запятой. Например, 0,75. Обыкновенная — дробь, компонентами которой являются числитель (вверху) и знаменатель (внизу). Например, 2/3.

Смешанные дроби записываются в виде целого числа и обыкновенной дроби. Например, 5 2/3. Эта форма записи применяется для приведения результата вычислений к нормальному виду. Например, при расчете некоторой величины получилась неправильная дробь 8/3. Ее можно записать в виде смешанной: 2 2/3. Чтобы опять привести ее к исходному значению, необходимо:

Компонентами рациональных чисел являются целые, натуральные, дробные и смешанные дроби. К иррациональным принадлежат любые значения, не входящие в состав рациональных. Следует отметить, что R представляются в виде степеней, радикалов (корней), тригонометрических функций и логарифмов.

Таким образом, все числа, используемые при расчетах и решения задач в различных дисциплинах с физико-математическим уклоном, называются действительными.

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №15. Действительные числа.

Перечень вопросов, рассматриваемых в теме

1) множество иррациональных чисел;

2) множество рациональных чисел;

3) правила выполнения действий с бесконечными десятичными дробями;

4)определение бесконечно убывающей геометрической прогрессии.

Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.

Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.

Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).

Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.

Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Все числа, которые мы изучаем в школе, называются действительными числами. Они образуют множество действительных чисел, которые принято обозначать латинской буквой R.

В свою очередь все действительные числа можно разделить на 2 группы: рациональные числа и иррациональные числа.

Иррациональные числа— это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.

Рациональные числа, в свою очередь, можно разделить на 2 вида – это целые числа и дробные числа.

Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.

Целые же числа можно разделить еще на несколько групп: отрицательные целые числа, нуль и положительные (натуральные) целые числа.

На числовой оси (Ох) между целыми числами будут находиться дробные иррациональные числа. Все вместе они будут представлять собой множество действительных чисел, R.

Обратите внимание, что все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).

Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.

Числа 4; 4,2; 4,28 и т.д. являются последовательными приближениями значений суммы

.

Пусть это последовательные приближения действительного числа у с точностью до 1, до 0,1, до 0,01 и т.д. Тогда погрешность приближения как угодно близко приближается к нулю.

при или

Читается «модуль разности у и стремится к нулю при n, стремящемся к бесконечности» или «предел модуля разности у и при n, стремящемся к бесконечности, равен нулю»

Т.е. если при или

Модуль действительного числа у обозначается как |у| и определяется так же, как и модуль рационально числа:

.

А теперь давайте вспомним, что такое геометрическая прогрессия.

Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего (Рисунок 1).

В результате, мы получили последовательность сторон квадратов образующих геометрическую прогрессию со знаменателем .

И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,

n=15, ;

n=20, ;

n=21, .

Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.

Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников. (рисунок 2)

Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.

То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.

Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.

Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.

Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.

Используя данное определение можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.

Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: (Рисунок 3)

Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.

Но в левой части этого равенства – сумма бесконечного числа слагаемых.

Рассмотрим сумму n первых слагаемых.

По формуле суммы n первых членов геометрической прогрессии, она равна

Если n неограниченно возрастает, то

или . Поэтому , т.е. .

Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности

Например, для прогрессии , где ,

имеем

Так как то

Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле

Примеры и разборы решений заданий тренировочного модуля

Пример 1:

Найдем значение данного выражения с точностью до единиц.

Округлим полученные результаты до десятых:

Найдем значение данного выражения с точностью до десятых.

Округлим полученные результаты до сотых:

3

Найдем значение данного выражения с точностью до сотых.

Округлим полученные результаты до тысячных:

32

и т.д.

Давайте выясним, является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:

а) ; б)

. Найдем q.

;;

Следовательно, данная геометрическая прогрессия является бесконечно убывающей.

Следовательно, данная последовательность не является бесконечно убывающей геометрической прогрессией.

Источник

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник