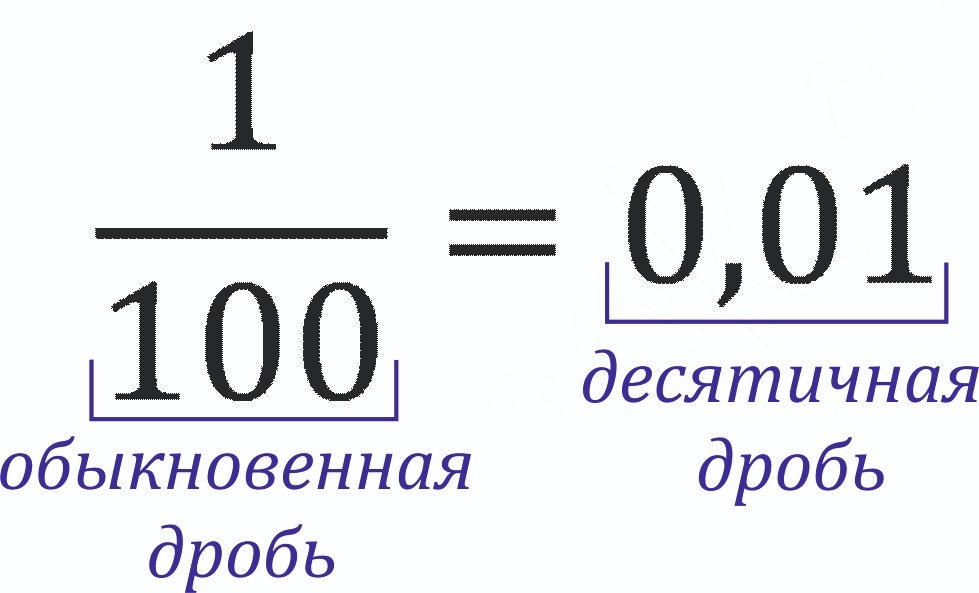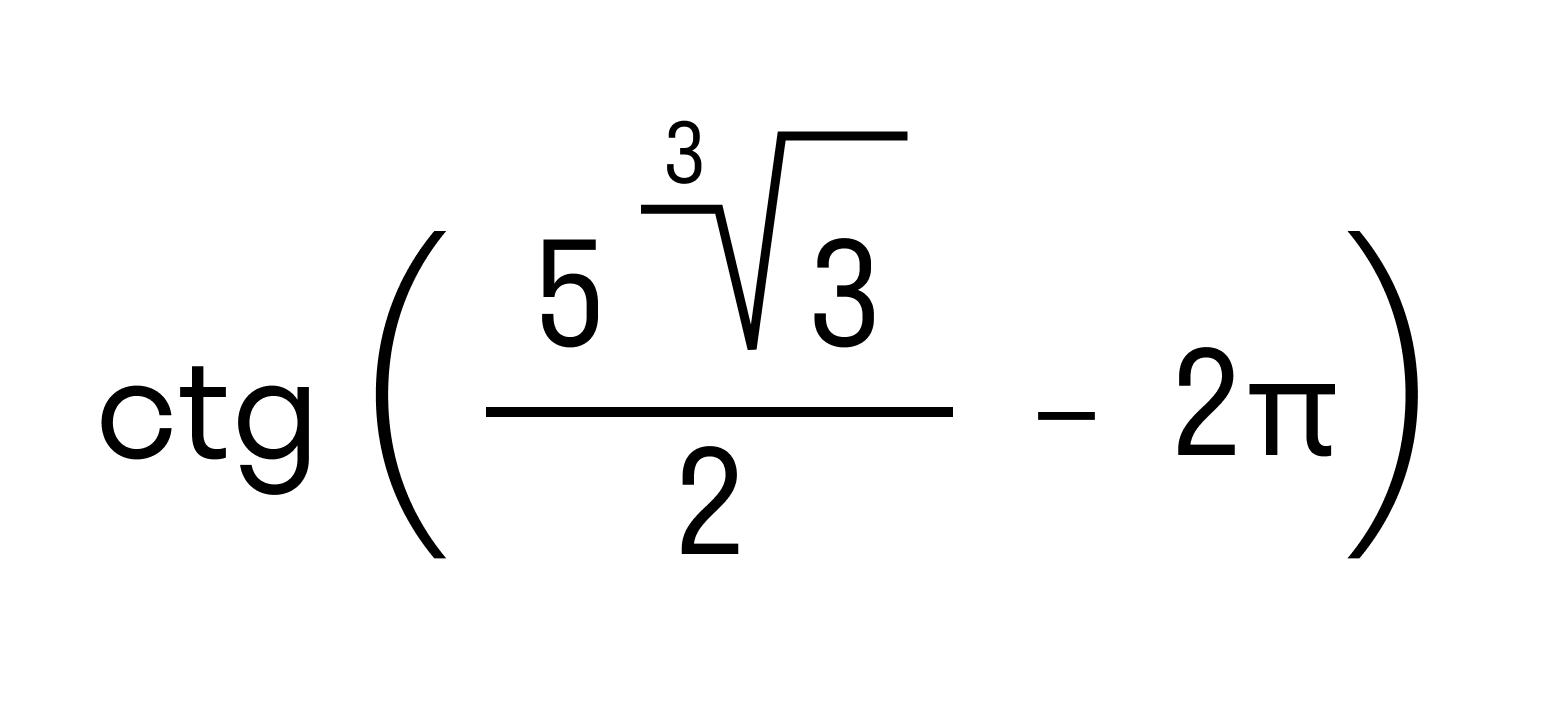Что такое действительные числа определение

Действительные числа, определение, примеры.

В данной статье собраны основные сведения про действительные числа. Сначала дано определение действительных чисел и приведем примеры. Дальше показано положение действительных чисел на координатной прямой. А в заключение разобрано, как действительные числа задаются в виде числовых выражений.

Навигация по странице.

Определение и примеры действительных чисел

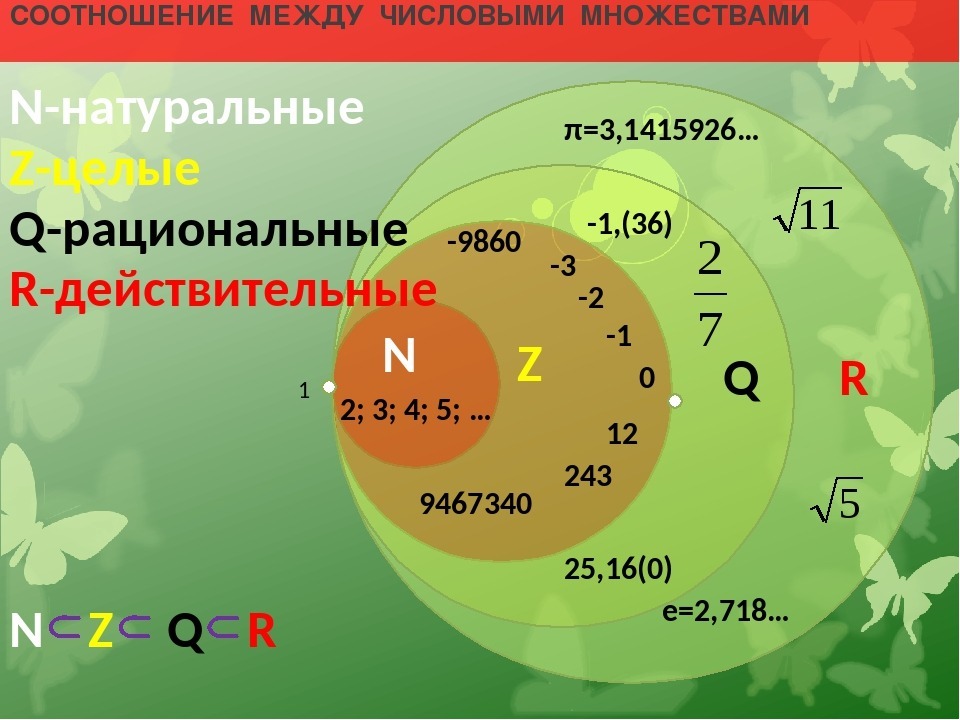
Подобно тому, как рациональные числа объединяют целые числа и дробные числа, действительные числа объединяют рациональные и иррациональные числа. Отсюда вытекает определение действительных чисел.

Действительные числа – это рациональные и иррациональные числа.

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то озвученное определение действительных чисел можно переформулировать следующим образом.

Действительные числа – это числа, которые могут быть записаны в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.

Из определения действительных чисел следует, что существуют как положительные, так и отрицательные действительные числа, а нуль – ни положительное, ни отрицательное действительное число.

Действительные числа позволяют описывать величины, значения которых могут изменяться непрерывно, чего не позволяют делать рациональные и иррациональные числа по отдельности. Другими словами, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное (эталонное) значение этой величины.

В заключение этого пункта заметим, что действительные числа также называют вещественными.

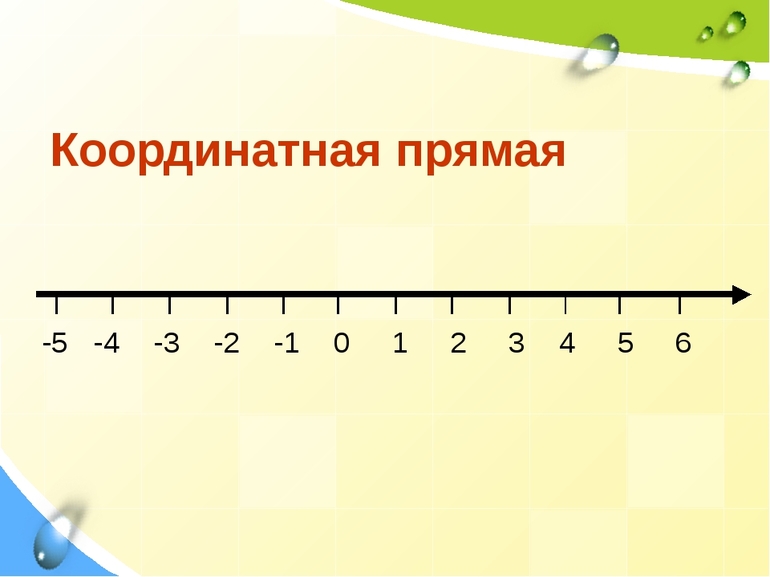
Действительные числа на координатной прямой

Действительные числа заполняют каждую точку координатной прямой. Каждой точке координатной прямой соответствует единственное действительное число – координата этой точки, а каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Действительные числа в виде выражений

А если пойти дальше, то из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций и т.п. можно составлять всевозможные числовые выражения, значения которых также будут действительными числами. Например, значения выражений и есть действительные числа.

В заключение этой статьи заметим, что следующим этапом расширения понятия числа является переход от действительных чисел к комплексным числам.

Источник

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Действительные числа

Что такое действительные числа

Действительное число — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функций.

Схематически понятие действительных значений можно представить совокупностью, образованной рациональными и иррациональными членами. Для наглядности этой совокупности прибегают к числовой прямой.

Стандартным условным обозначением является буква R, выполненная полужирным шрифтом.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Обозначение не случайное, оно взято из английского слова realis (в переводе — действительный).

С позиции конструктивизма вещественные величины для математики не являются строгими понятиями. Их вводят для арифметических операций или определения отношений в каком-либо порядке, а также для доказательства проявляемых свойств.

По своей сути действительное число является бесконечной десятичной дробью. Его можно записать следующим образом:

Как обычно, значение до первой запятой — целое. Если в каком-либо сегменте после запятой образуются нули, они не пишутся.

Если захотеть представить, между какими рациональными величинами находится выражаемое значение, то это будет выглядеть так:

ао, а1, а2….. аn и ао, а1, а2….. аn+10-n

Где n — значение натурального числа.

История термина

Введение в обиход термина «вещественное число» произошло еще в Древней Греции. Школа Пифагора обратила внимание, что, кроме целых значений и их соотношений, существует несоизмеримое множество. С точки зрения современных классификаций, это — числа, не являющиеся рациональными.

Позднее Евдокс Книдский пытался создать общую теорию, которая бы включала также несоизмеримые величины. Однако в практику эти попытки в то время не вошли. Прошло более двух тысяч лет, пока возникла истинная необходимость введения такого понятия. Толчком послужил математический анализ, развиваемый Р.Дедекиндом, Г.Кантором, Э.Гейне и их коллегами. Периодом создания теории вещественных (или действительных) чисел считается вторая половина XIX века.

Для современных математиков то множество, которое объединяет рациональные и иррациональные величины, является непрерывным упорядоченным полем. С позиции изоморфизма оно является единственным.

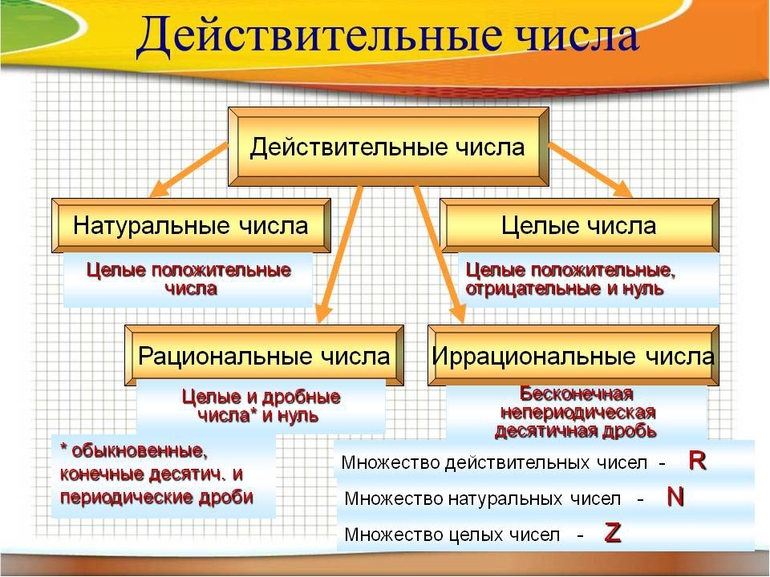
Представления действительных чисел

Как видно из рисунка из действительных выделяют рациональные и иррациональные величины.

Рациональные (Q), в свою очередь, подразделяются на целые (Z) и дробные. В совокупность целых входят ноль, натуральные значения (N) и им противоположные.

Самое простое, что можно представить в математике — это натуральное число. Это то, что мы перечисляем при простом счете. Именно с этих чисел дети начинают учиться решать элементарные примеры. Они же используются в сложнейших математических задачах. Если выстроить натуральные единицы в порядке возрастания, получится натуральный ряд. Он является бесконечным, поскольку после n всегда существует n+1.

Отрицательные числа не относятся к натуральным, ими не получится объективно считать.

Существует две теории определения группы натуральных чисел. Согласно первой, они появляются, когда человек что-либо нумерует. Например: первый, второй, третий и последующий участник. Согласно второй, в них есть необходимость в ситуациях, когда нужно определиться с количеством чего-либо. Например, 1 стул, 0 стульев, 100 стульев. Казалось бы, оба подхода определяют натуральные числа, однако явно заметна разница: в первом случае ноль исключен, во втором — без него не обойтись.

Поэтому сегодня существует два условных обозначения для этой группы:

Характеризуя натуральные числа, обращают внимание на их свойства:

Целые числа

Взяв натуральное множество, включающее нуль и добавив к нему отрицательные значения, получим новую единицу классификации — целые числа. При этом возникает резонный вопрос: зачем нужно дополнительное понятие? Продиктована эта необходимость тем, что, работая с натуральными числами, вычесть из меньшего большее нереально. С целыми это сделать можно.

Действительное значение можно сделать целым при сокращении его дробной части. Так, 7,5 или 124,85 не являются целыми, 2, 8, 12, 154 — являются.

Для обозначения множества целых чисел применяется Z. В математике существует раздел «Теория чисел», который занимается изучением их характеристик.

Структуру множества целых можно представить тремя составляющими:

Натуральные заметны при счете, например, 1, 2, 3 и т.д. Отрицательные имеют впереди знак «-». Для всех целых чисел существует противоположное значение со знаком минус. При этом абсолютная величина числа не содержит минуса. Ее правильным обозначением является ׀a׀.

В решениях задач для целых величин предусматриваются такие действия:

При этом деление может осуществляться с остатком. Целые могут сравниваться друг с другом, при этом Z — это линейно упорядоченное, бесконечное множество. Его мощность идентична мощности натуральных чисел. Оба они применяются для счета.

Десятичные дроби

Не всякую величину можно измерить целыми единицами. Если, кроме него, в значении включена дополнительно ее часть, то такая величина является дробной.

Десятичные дроби записываются так: 5,6; 7,88; 9,2568. Разрядность после запятой может быть различной, но в любом случае десятичная дробь не может иметь знаменателя. Другими словами, он равен 0 целых и 0 десятых.

После запятой могут стоять абсолютно разные цифры. Их значение определяется местом, на котором они расположены после запятой. Так, в десятичной дроби 5,123 цифра 1 соответствует десятым, 2 — сотым, 3 — тысячным и так далее. Если какой-либо ранг пропущен, вместо него обязательно ставится нуль. Так, в числе 5,208 десятым соответствует 2, а тысячным — 8. Сотые в данном примере отсутствуют.

Десятичная дробь может быть конечной либо бесконечной. Схематическая запись конечной выглядит так: ao,a1, a2…an. Число цифр после запятой четко определено.

Примером бесконечной является число π. Его значение равняется 3,1415926535897…Из примера видно, что количество цифр после запятой не определено, т.е. ao, a1, a2…

Бесконечная десятичная дробь может характеризоваться периодичностью. В таком случае в цифрах после запятой наблюдается периодически повторяющаяся группа цифр.

В таком случае цифры 456 называются периодом дроби, а количество цифр в группе (3 цифры) — длина периода.

Появлением десятичных дробей мы обязаны Китаю, когда там, в III веке н.э. считали на счетных досках. Позднее, трактат «Ключи арифметики», от имени Дж. Гияс-ад-дин-аль-Каши (математик и астроном) объявил об их официальном открытии. В Европе первым объявил об их существовании И. Бонфис (1350 год), а пользоваться ими стали в 1585 году, по мере выхода труда Стевина «Десятая».

Обыкновенные дроби

Говоря о дроби, математики имеют ввиду число, которое состоит из одной, двух либо нескольких одинаковых по величине частей от единицы. Эти части называются долями.

Кроме рассмотренных выше десятичных дробей, существуют обыкновенные, схематически выражаемые формулой m/n. Они могут иметь знак «-» либо «+». Значение цифр в обыкновенной дроби следующее: над чертой — числитель (показывает сколько раз взята выбранная доля), под чертой — знаменатель (то, насколько частей разделили первоначальное число).

Дробь, в которой целый числитель и знаменатель отличный от нуля, относится к рациональным числам.

Обыкновенные дроби представлены правильными и неправильными вариантами. Если числитель меньше (по модулю), чем знаменатель, то эта дробь правильная Если наоборот — неправильная (тогда она — рациональное число, которое по модулю превышает либо равно единице).

Различают также смешанные дроби. В их записи присутствует целое число и правильная дробь. Простым языком можно сказать, что смешанная дробь по своему значению равна сумме целого числа и дроби.

Более сложной модификацией является дробь составная, т.е. «многоэтажная». В ней числитель и знаменатель (либо только один из них) также представлены обыкновенными дробями.

С обыкновенными дробями можно производить следующие действия:

То, как обозначаются обыкновенные дроби сегодня, пришло из Древней Индии. Вначале разделительная черта не использовалась, но цифры писались одна под другой. Черта появилась лишь 300 лет назад, с подачи итальянского купца Фибоначчи. Уверенное пользование такими цифрами началось после выхода труда Стевина «Десятая».

Координатная прямая и действительные числа

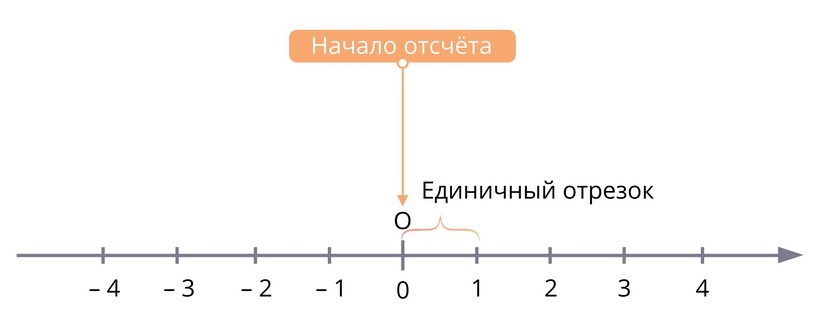
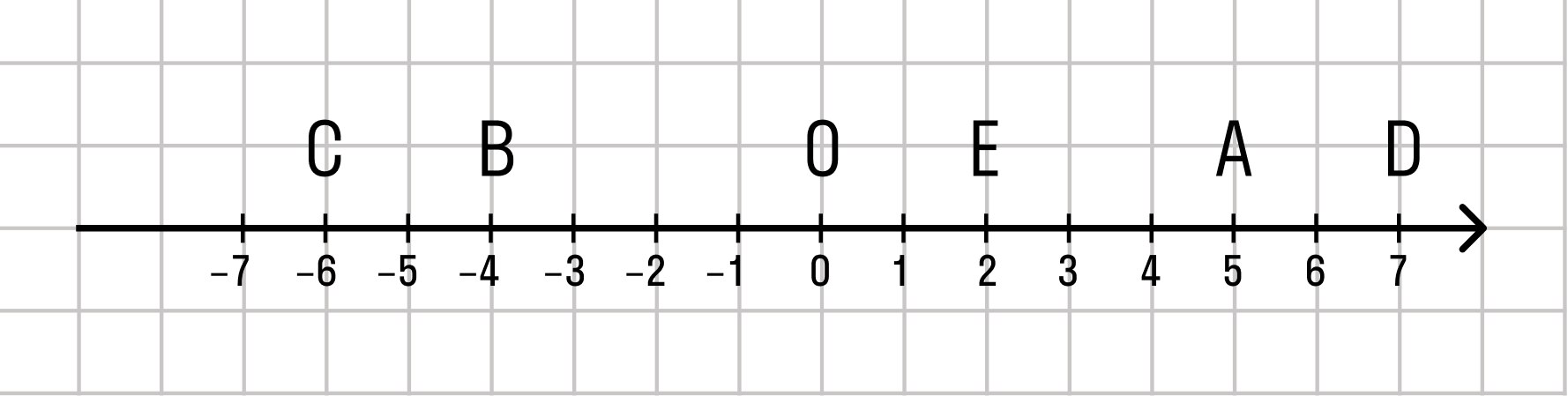
Для решения многих математических задач удобно построить схему, на которой отразить месторасположение какого-либо тела с известными координатами. Если действие можно произвести по одной прямой линии, действительные числа располагаются на ней через равные промежутки, принятые за единицу измерения. Такое изображение называется числовой прямой. На ней обязательно существует 0 (точка отсчета) и единицы измерения — действительные числа — расположенные в порядке возрастания либо убывания (как на рисунке).

Прямая с нанесенными на ней началом отсчета, направлением отсчета и отрезками равной длины называется осью координат. При этом вправо от 0 всегда направлена положительная координатная полуось, а влево — отрицательная.

Координата — число, которое определяет нахождение точки (либо тела) на координатной оси.

С помощью координатной прямой и действительных чисел, нанесенных на ней, можно определять не только местоположение точки, но и сравнивать ее с другими точками, отображать ее координаты в процессе движения.

Координатную прямую часто называют геометрической моделью всего множества действительных чисел. Второе ее название — числовая прямая.

Правила вычисления с действительными числами, формулы

Действительные значения могут участвовать как в простых математических задачах, так и сложных, преобразовательных и упрощаемых заданиях.

Для них действуют формулы типа: a больше (либо меньше) числа b, если при вычитании b из a получается положительная (либо отрицательная) величина.

Кроме того в работе с действительными числами пользуются правилами:

Существуют и правила для сравнения действительных чисел:

Иногда для простоты расчетов прибегают к округлению действительных чисел. При большой разрядности исходного в условии обычно оговаривается до каких единиц произвести округление. Если последующая цифра за заданным рангом 5 и больше, то округление происходит с увеличением, если меньше — с уменьшением.

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Общие сведения

Результатом математических операций (деления, произведения, сложения, вычитания, возведением в степень и т. д. ) могут быть действительные числа. Примерами являются любые значения. Действительное число — совокупность рациональных и иррациональных величин. Международное обозначение — литера «R».

Следует отметить, что рациональные величины представляются в виде десятичной (конечной) или бесконечной периодической десятичной дроби. В первом случае число имеет определенное количество знаков после запятой, результат которого получен при делении двух значений. Например, 8/5 = 1,6. Последняя величина ограничена десятыми долями.

Бесконечная десятичная периодическая дробь представляет собой вещественную величину с бесконечным количеством знаков после запятой. Например, при делении 5 на 3 получается результат, равный 1,(6). Запись читается таким образом: одна целая и 6 в периоде.

В случае иррациональных чисел — бесконечные непериодические дроби, т. е. после запятой идет бесконечная запись, которая не повторяется вообще. Например, 1,213456789523648 и так до бесконечности.

На основании этой информации можно получить другое определение: действительные — это числа, которые можно записать в виде конечной или бесконечной десятичной дроби. Кроме того, нуль принадлежит также множеству R. Он является единственным значением, которое не является положительным и отрицательным. В некоторых источниках можно также встретить другое название действительных чисел — вещественные.

Координатная прямая

Для представления положения любого R применяется координатная прямая, являющаяся их геометрическим смыслом. Величины на ней отмечаются в порядке возрастания. Перед построением следует начертить произвольную прямую, а затем отметить на ней точку 0 (нулевую отметку). После этого можно приступить к откладыванию числовых значений. Слева от нулевой координаты расположены отрицательные, а справа — положительные числа.

Из курса геометрии 5 класса можно вспомнить следующее определение: прямой называется произвольное геометрическое место точек, расположенных в один ряд до бесконечности. Иными словами, прямая — линия, не имеющая начала и конца, т. е. она не ограничена в пространстве.

Координатную прямую используют при решении дифференциальных уравнений, неравенств, поиска области значения функции и т. д.

Представление действительных чисел

Для представления действительных чисел следует разобрать значения, которые к ним относятся. Эта классификация рекомендована математиками. Она имеет такой вид:

К первой группе относятся числа, которые изобрели древние греки. Их еще называют природными. Они применяются при сложных вычислениях на рынках, магазинах и других разнообразных расчетах. Во вторую категорию входят все целые (положительные и отрицательные) и 0. Дробные состоят из десятичных и обыкновенных дробей. К первым относятся значения, состоящие из целой и дробной частей. Последние отделяются посредством запятой. Например, 0,75. Обыкновенная — дробь, компонентами которой являются числитель (вверху) и знаменатель (внизу). Например, 2/3.

Смешанные дроби записываются в виде целого числа и обыкновенной дроби. Например, 5 2/3. Эта форма записи применяется для приведения результата вычислений к нормальному виду. Например, при расчете некоторой величины получилась неправильная дробь 8/3. Ее можно записать в виде смешанной: 2 2/3. Чтобы опять привести ее к исходному значению, необходимо:

Компонентами рациональных чисел являются целые, натуральные, дробные и смешанные дроби. К иррациональным принадлежат любые значения, не входящие в состав рациональных. Следует отметить, что R представляются в виде степеней, радикалов (корней), тригонометрических функций и логарифмов.

Таким образом, все числа, используемые при расчетах и решения задач в различных дисциплинах с физико-математическим уклоном, называются действительными.

Источник