Что такое делительная окружность
Детали машин
Геометрические параметры эвольвентного зацепления
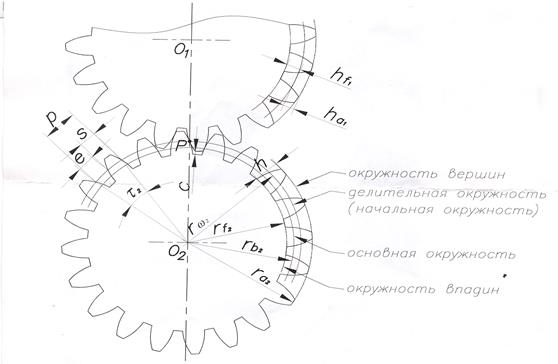
Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.
В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:
Параметрам, относящимся к делительной окружности, индекс не присваивается.
Начальные окружности
Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О1 и О2 до полюса П ) при неизменном межосевом расстоянии О1О2 тоже остается неизменным.
При изменении межосевого расстояния aw меняются и диаметры dw начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.
Межосевое расстояние определяется по формуле:
Делительная окружность
Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.
Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.
У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:
Исключение составляют передачи с угловой модификацией.
Окружной шаг зубьев
Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.
Основной шаг
Окружная толщина зуба и окружная ширина впадины
Окружной модуль зубьев
Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.
Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).
При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.
Высота головки и ножки зуба
Длина активной линии зацепления
Коэффициент торцового перекрытия
Коэффициентом торцового перекрытия εα называют отношение длины активной линии зацепления к основному шагу:
где z1 и z2 – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.
Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.
Делительная окружность
Смотреть что такое «Делительная окружность» в других словарях:
ДЕЛИТЕЛЬНАЯ ОКРУЖНОСТЬ — окружность зубчатого колеса, по к рой шаг зубьев р= Пи*т, где т стандартный торцевой модуль зубьев(см. рис.). Д. о. в торцевом сечении делит зуб на головку и ножку. К ст. Делительная окружность: d диаметр делительной окружности; р шаг зубьев … Большой энциклопедический политехнический словарь
делительная окружность — standard cirle of cylindrical gear Окружность, которая является базовой для определения размеров зубьев цилиндрического зубчатого колеса. Шифр IFToMM: Раздел: СТРУКТУРА МЕХАНИЗМОВ … Теория механизмов и машин
делительная окружность плоского колеса — Окружность пересечения делительной плоскости плоского колеса дополнительным цилиндром. Примечания: 1. Различают внешнюю, среднюю, внутреннюю и др. делительные окружности плоского колеса, соответствующие внешнему, среднему, внутреннему и др.… … Справочник технического переводчика
Делительная окружность кабельного изделия — 196. Делительная окружность кабельного изделия Делительная окружность Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Источник: ГОСТ 15845 80: Изделия кабельные. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Делительная окружность плоского колеса — 78. Делительная окружность плоского колеса Окружность пересечения делительной плоскости плоского колеса дополнительным цилиндром. Примечания: 1. Различают внешнюю, среднюю, внутреннюю и др. делительные окружности плоского колеса, соответствующие… … Словарь-справочник терминов нормативно-технической документации
Делительная окружность кабельного изделия — 1. Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Употребляется в документе: ГОСТ 15845 80 Изделия кабельные. Термины и определения … Телекоммуникационный словарь
Окружность, делительная — Делительная окружность Окружность, проходящая через центры элементов скрутки (проволок, стренг, жил, групп, пучков), образующих повив Смотреть все термины ГОСТ 15845 80. ИЗДЕЛИЯ КАБЕЛЬНЫЕ. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ Источник: ГОСТ 15845 80. ИЗДЕЛИЯ… … Словарь ГОСТированной лексики
Окружность кабельного изделия, делительная — Делительная окружность кабельного изделия … Словарь ГОСТированной лексики
концентрическая окружность конического зубчатого колеса — концентрическая окружность Одна из окружностей пересечения однотипных соосных конусов делительным* (начальным) дополнительным конусом. Примечания 1. Различают концентрические окружности: внешнюю, среднюю, внутреннюю и др. делительные; внешнюю,… … Справочник технического переводчика
2.3. ЭВОЛЬВЕНТНЫЕ ЗУБЧАТЫЕ КОЛЕСА И ИХ ПАРАМЕТРЫ
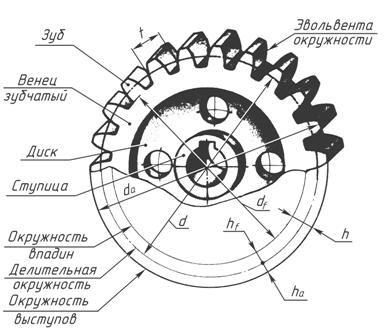
Рисунок 3. Параметры эвольвентного зубчатого колеса.
К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.
Виды модулей: делительный, основной, начальный.
Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.
Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.
Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения
Делительная окружность делит зуб на головку и ножку.
Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.
Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.
Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.
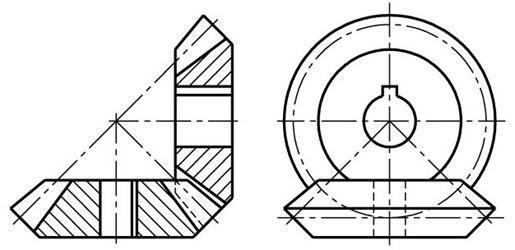
Сумма высот головки ha и ножки hf соответствует высоте зубьев h:
Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.
Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.
Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.
Коэффициент уравнительного смещения Δу:
Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.
Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу
Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев
Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба
S = 0,5 · ρ + 2 · х · m · tg α
Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев
Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.
Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.
Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра
Зубчатого колеса
Окружность вершин — окружность, описанная из центра колеса и ограничивающая вершины зубьев.
Окружность впадин — окружность, описанная из центра колеса и ограничивающая его впадины со стороны колеса.
Делительная окружность— окружность, на которой расстояние между одноименными сторонами двух соседних зубьев равно шагу зуборезного инструмента. Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.
Модуль — значение следует выбирать по СТ СЭВ-310-76. Этим стандартом дан ряд значений от 0,05 до 100 мм:
— 1 ряд (предпочтительный): 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25 и т. д.;- 2 ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; И; 14; 18; 22 и т. д.
Окружной шаг зубчатого зацепления р – есть расстояние между одноименными точками двух соседних зубьев колеса, измеренное по дуге делительной окружности.
Высотой зуба h – называется радиальное расстояние между окружностью вершин и окружность впадин.
Разница в высоте ножки зуба одного колеса и высоте головки зуба другого необходима для образования радиального зазора:
Теоретически толщина зуба s и ширина впадины e по делительной окружности равны между собой:
Однако, чтобы создать боковой зазор, необходимый для нормальной работы зубчатой пары, зуб делается несколько тоньше, вследствие чего он входит во впадину свободно.
Межосевое расстояние двух сцепляющихся зубчатых колес определяется по формуле:
Передаточное отношение (основной закон зацепления):
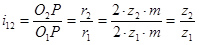
| № п/п | Название | Формула для вычисления (без смещения режущего инструмента) |
| Диаметр окружности вершин | 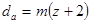 | |
| Диаметр окружности впадин | 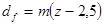 | |
| Диаметр основной окружности | 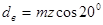 | |
| Диаметр начальной окружности | 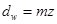 | |
| Диаметр делительной окружности | 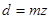 | |
| Модуль | m | |
| Число зубьев | z | |
| Шаг по делительной окружности | 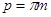 | |
| Высота зуба | 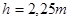 | |
| Высота головки зуба | 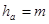 | |
| Высота ножки зуба | 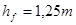 | |
| Толщина зуба по делительной окружности | 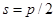 | |
| Ширина впадины между зубьями по делительной окружности | 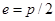 | |
| Угловой шаг | 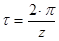 |
Методы изготовления эвольвентных зубчатых колёс
В основу изготовления эвольвентных зубчатых колёс положено два принципиально отличительных метода.
Способ копирования
Рабочие кромки инструмента по форме соответствуют обрабатываемой поверхности (подобны ей, то есть заполняют эту поверхность как отливка заполняет форму).
Нарезание зубчатых колес осуществляется профилированной пальцевой 1 или дисковой 2 фрезами (рис.5.3 а, б), проекция режущих кромок которых соответствует конфигурации впадин. Резание производится в следующем порядке: прорезается впадина первого зуба, затем заготовка с помощью делительного устройства (делительной головки) поворачивается на угловой шаг и прорезается следующая впадина. Операции повторяются до тех пор, пока не будут прорезаны все впадины.
Достоинства:
1.Возиожность нарезания зубьев 6на универсальном фрезерном оборудовании.
Недостатки:
1.Огромная номенклатура режущего инструмента (равна сочетанию модуля и числа зубьев);
2.Принципиальная неточность нарезания зубьев;
3.Нетехнологичность инструмента, малая производительность.
Способ огибания (обкатки)
Достоинства:
1.Принципиальная точность нарезания зубьев;
2.Резкое сокращение номенклатуры и технологичность инструмента;
Недостатки:
1.Требуется специальное зубонарезное оборудование.
Глава 8. зацепления зубчатые
 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
где z – число зубьев;
Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
где t – шаг зацепления.
Диаметр окружности выступов зубьев :
Диаметр окружности впадин :
Служит для передачи вращения при параллельных осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Служит для преобразования вращательного движения в возвратно-поступательное.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращательного движения между валами со скрещивающимися осями.
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Служит для передачи вращения при пересекающихся осях валов.
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.






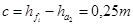
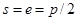
 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.