Что такое быстрое преобразование фурье

Понимание алгоритма БПФ

Здравствуйте, друзья. Уже завтра стартует курс «Алгоритмы для разработчиков», а у нас остался один неопубликованный перевод. Собственно исправляемся и делимся с вами материалом. Поехали.

Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.

Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.

Дискретное преобразование Фурье

БПФ — это быстрый алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:

Прямое дискретное преобразование Фурье (ДПФ):

Обратное дискретное преобразование Фурье (ОДПФ):

Преобразование из xn → Xk является переводом из конфигурационного пространства в пространство частотное и может быть очень полезным как для исследования спектра мощности сигнала, так и для преобразования определенных задач для более эффективного вычисления. Некоторые примеры этого в действии вы можете найти в главе 10 нашей будущей книги по астрономии и статистике, где также можно найти изображения и исходный код на Python. Пример использования БПФ для упрощения интегрирования сложных в противном случае дифференциальных уравнений смотрите в моем посте «Решение уравнения Шредингера в Python».

Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях numpy.fft и scipy.fftpack соответственно. Самый быстрый БПФ, о котором я знаю, находится в пакете FFTW, который также доступен в Python через пакет PyFFTW.

На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.

Вычисление дискретного преобразования Фурье

Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор

с матрицей М, заданной

Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:

Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:

Просто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:

Мы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как , в то время как наш медленный алгоритм масштабируется как . Это означает, что для элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!

Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.

Симметрии в дискретном преобразовании Фурье

Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении . Из нашего выражения выше:

где мы использовали тождество exp [2π i n] = 1, которое выполняется для любого целого числа n.

Последняя строка хорошо показывает свойство симметрии ДПФ:

для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.

ДПФ в БПФ: использование симметрии

Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:

Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ∗ N вычислений, всего .

Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0≤k True

Сопоставим этот алгоритм с нашей медленной версией:
-In [6]:

Наш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически : мы реализовали быстрое преобразование Фурье.

Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за fft numpy, — это реализация на Фортране, которая получила годы доработок и оптимизаций. Кроме того, наше решение NumPy включает в себя как рекурсию стека Python, так и выделение множества временных массивов, что увеличивает время вычислений.

Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.

Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:

Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:

Поскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя DFT_slow :
In [9]:

Мы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.

Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.

Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.

Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.

Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.

Источник

Быстрое преобразование Фурье

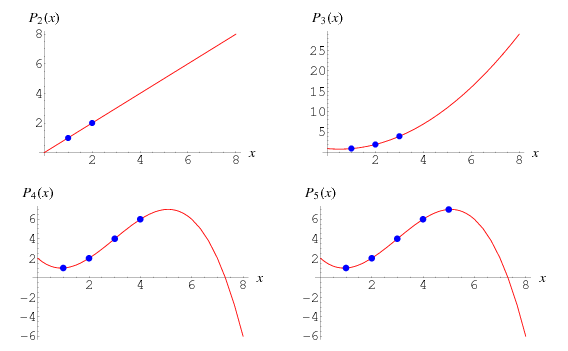
Рассмотрим такую распространённую операцию как умножение двух целых чисел. Квадратичный алгоритм — умножения в столбик — все знают со школы. Долгое время предполагалось, что ничего быстрее придумать нельзя.

\[ T(n)=3T\left(\dfrac n 2\right)+O(n)=O\left(n^<\log_2 3>\right)\approx O(n^<1.58>) \]

Чтобы перейти к алгоритму с лучшей оценкой, нам нужно сначала установить несколько фактов о многочленах.

Умножение многочленов

Обратим внимание на то, что любое число можно представить многочленом:

\[ \begin A(x) &= a_0 + a_1\cdot x + a_2 \cdot x^2 + \dots + a_n \cdot x^n \\ &= a_0 + a_1\cdot 2 + a_2 \cdot 2^2 + \dots + a_n \cdot 2^n \end \]

Основание x при этом может быть выбрано произвольно.

Чтобы перемножить два числа, мы можем перемножить соответствующие им многочлены, а затем произвести каррирование: пройтись от нижних разрядов получившегося многочлена и «сдвинуть» переполнившиеся разряды:

Прямая формула для произведения многочленов имеет вид

\[ \left(\sum_^n a_i x^i\right)\cdot\left(\sum_^m b_j x^j\right)=\sum_^x^k\sum_a_i b_j \]

Её подсчёт требует \(O(n^2)\) операций, что нас не устраивает. Подойдём к этой задаче с другой стороны.

Интерполяция

Доказательство будет конструктивным — можно явным образом задать многочлен, который принимает заданные значения \(y_0, y_1, \ldots, y_n\) в этих точках:

Корректность. Проверим, что в точке \(x_i\) значение действительно будет равно \(y\) :

Этот многочлен называется интерполяционным многочленом Лагранжа, а сама задача проведения многочлена через точки — интерполяцией.

\[ \begin 1 & x_0 & x_0^2 & \ldots & x_0^n \\ 1 & x_1 & x_1^2 & \ldots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \ldots & x_n^n \\ \end \]

Умножение через интерполяцию

Если притвориться, что evaluate и interpolate работают за линейное время, то умножение тоже будет работать за линейное время.

Но что, если бы мы могли вычислять значения в точках и делать интерполяцию быстрее?

Комплексные числа

С комплексными числами можно работать почти так же, как с действительными. Они даже удобнее: все квадратные корни всегда извлекаются, все корни многочленов всегда находятся.

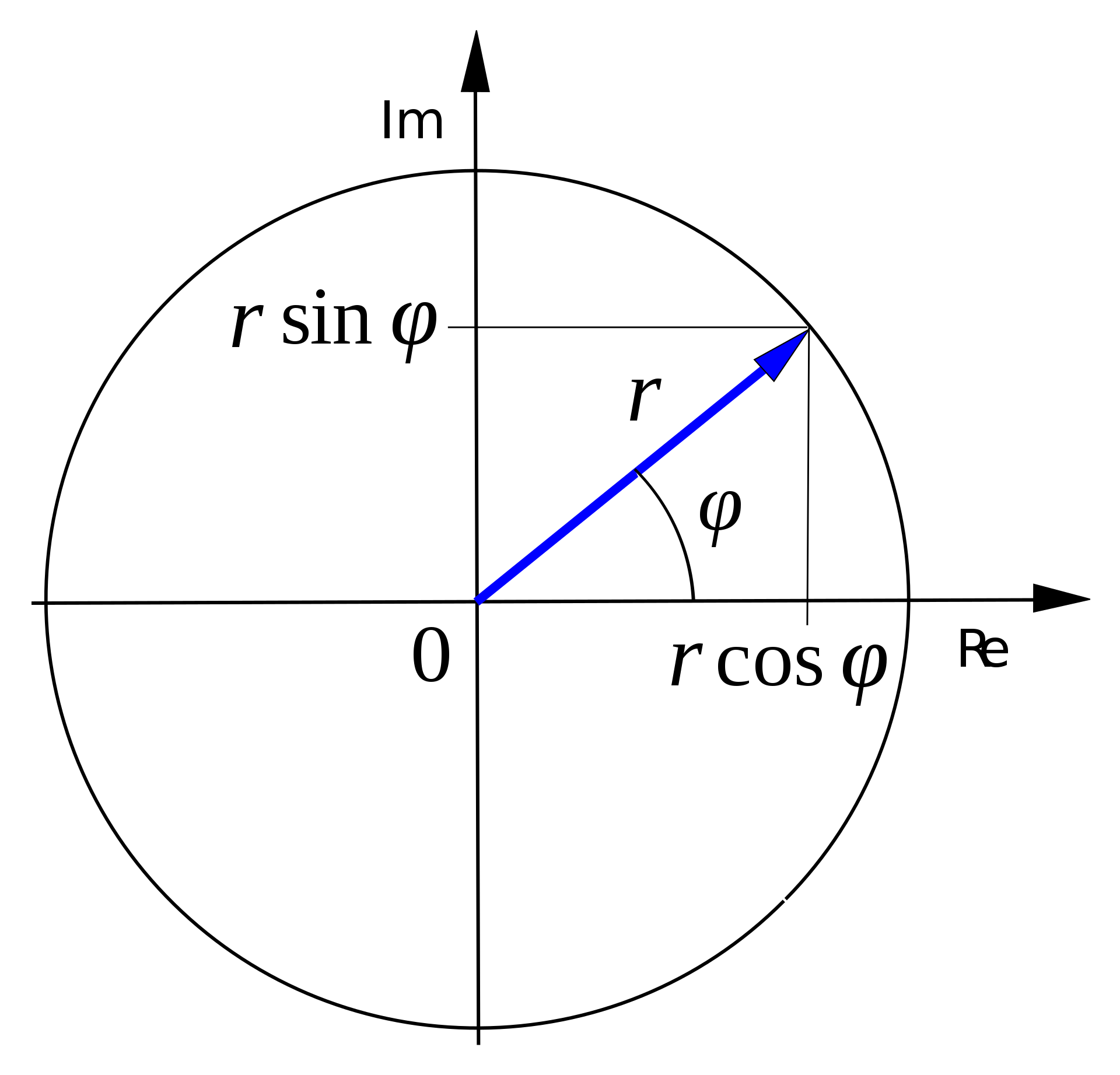
Комплексная плоскость

Комплексные числа удобно изображать на плоскости в виде вектора \((a, b)\) и считать через них всякую геометрию.

Таким образом комплексное число можно представить в полярных координатах:

\[ a+bi = r ( \cos \phi + i \sin \phi ) \]

Подобное представление удобно по следующей причине: чтобы перемножить два комплексных числа, нужно перемножить их модули и сложить аргументы.

Упражнение. Докажите это.

Формула эйлера

Определим число Эйлера \(e\) как число со следующим свойством:

\[ e^ = \cos \phi + i \sin \phi \]

Геометрически, все такие точки живут на единичном круге:

\[ (\cos a + i \sin a) \cdot (\cos b + i \sin b) = e^ \]

Упражнение. Проверьте это: раскройте скобки и проделайте немного алгебры.

Корни из единицы

У комплексных чисел есть много других замечательных свойств, но нам для алгоритма на самом деле потребуется только следующее:

А именно, это будут числа вида:

На комплексной плоскости эти числа располагаются на единичном круге на равном расстоянии друг от друга:

Все 9 комплексных корней степени 9 из единицы

Упражнение. Докажите, что других корней быть не может.

Дискретное преобразование Фурье

Дискретным преобразованием Фурье называется вычисление значений многочлена в комплексных корнях из единицы:

Почему эта формула верна? При вычислении ПФ мы практически применяем матрицу к вектору:

\[ \begin w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^1 & w^2 & w^3 & \dots & w^ <-1>\\ w^0 & w^2 & w^4 & w^6 & \dots & w^ <-2>\\ w^0 & w^3 & w^6 & w^9 & \dots & w^ <-3>\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^ <-1>& w^ <-2>& w^ <-3>& \dots & w^1 \end\begin a_0 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_ \end = \begin y_0 \\ y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_ \end \]

\[ W^ <-1>= \dfrac 1 n\begin w^0 & w^0 & w^0 & w^0 & \dots & w^0 \\ w^0 & w^ <-1>& w^ <-2>& w^ <-3>& \dots & w^ <1>\\ w^0 & w^ <-2>& w^ <-4>& w^ <-6>& \dots & w^ <2>\\ w^0 & w^ <-3>& w^ <-6>& w^ <-9>& \dots & w^ <3>\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ w^0 & w^ <1>& w^ <2>& w^ <3>& \dots & w^ <-1>\end \]

Проверим, что при перемножении \(W\) и \(W^<-1>\) действительно получается единичная матрица:

Зачем это надо?

Напомним, что мы изначально хотели перемножать многочлены следующим алгоритмом:

Посчитаем значения в \(n+m\) каких-нибудь точках обоих многочленов

Интерполяцией получим многочлен-произведение.

В общем случае быстро посчитать интерполяцию и даже просто посчитать значения в точках нельзя, но для корней единицы — можно. Если научиться быстро считать значения в корнях и интерполировать (прямое и обратное преобразование Фурье), но мы можно решить исходную задачу.

Схема Кули-Тьюки

Обычно, алгоритмы «разделяй-и-властвуй» делят задачу на две половины: на первые \(\frac<2>\) элементов и вторые \(\frac<2>\) элементов. Здесь мы поступим по-другому: поделим все элементы на чётные и нечётные.

Зная это, исходную формулу для значения многочлена в точке \(w^t\) можно записать так:

У нас по сути в два раза меньше корней (но они так же равномерно распределены на единичной окружности) и в два раза меньше коэффициентов — мы только что успешно уменьшили нашу задачу в два раз.

\[ T(n)=2T\left(\dfrac n 2\right)+O(n)=O(n\log n) \]

Заметим, что предположение о делимости \(n\) на \(2\) имело существенную роль. Значит, \(n\) должно быть чётным на каждом уровне, кроме последнего, из чего следует, что \(n\) должно быть степенью двойки.

Реализация

Приведём код, вычисляющий БПФ по схеме Кули-Тьюки:

Как обсуждалось выше, обратное преобразование Фурье удобно выразить через прямое:

Теперь мы умеем перемножать два многочлена за \(O(n \log n)\) :

Читателю рекомендуется самостоятельно задуматься о том, как можно улучшить время работы и точность вычислений. Из наиболее важных недостатков:

внутри преобразования не должно происходить выделений памяти

работать желательно с указателями, а не векторами

корни из единицы должны быть посчитаны наперёд

Следует избавиться от операций взятия остатка по модулю

Здесь приведена одна из условно пригодных реализаций.

Но главная проблема в численной стабильности — мы нарушили первое правило действительных чисел. Однако, от неё можно избавиться.

Number-theoretic transform

Нам от комплексных чисел на самом деле нужно было только одно свойство: что у единицы есть \(n\) «корней». На самом деле, помимо комплексных чисел, есть и другие алгебраические объекты, обладающие таким свойством — например, элементы кольца вычетов по модулю.

\[ m = 998244353 = 7 \cdot 17 \cdot 2^ <23>+ 1 \]

Реализация практически не отличается.

Применения

Источник

Преобразование Фурье в действии: точное определение частоты сигнала и выделение нот

Начнём с пианино. Очень упрощёно этот музыкальный инструмент представляет собой набор белых и чёрных клавиш, при нажатии на каждую из которых извлекается определённый звук заранее заданной частоты от низкого до высокого. Конечно, каждый клавишный инструмент имеет свою уникальную тембральную окраску звучания, благодаря которой мы можем отличить, например, аккордеон от фортепиано, но если грубо обобщить, то каждая клавиша представляет собой просто генератор синусоидальных акустических волн определённой частоты.

Когда музыкант играет композицию, то он поочерёдно или одновременно зажимает и отпускает клавиши, в результате чего несколько синусоидальных сигналов накладываются друг на друга образуя рисунок. Именно этот рисунок воспринимается нами как мелодия, благодаря чему мы без труда узнаём одно произведение, исполняемое на различных инструментах в разных жанрах или даже непрофессионально напеваемое человеком.

Наглядная иллюстрация нотного рисунка

Определение частоты (режим гитарного тюнера)

Обратная задача состоит в том, чтобы разобрать звучащую музыкальную композицию на ноты. То есть разложить суммарный акустический сигнал, улавливаемый ухом, на исходные синусоиды. По сути, этот процесс и представляет собой прямое преобразование Фурье. А нажатие на клавиши и извлечение звука есть процесс обратного преобразования Фурье.

Математически в первом случае происходит разложение сложной периодической (на некотором временном интервале) функции в ряд более элементарных ортогональных функций (синусоид и косинусоид). А во втором их обратное суммирование, то есть синтез сложного сигнала.

Ортогональность, в некотором роде, обозначает несмешиваемость функций. Например, если мы возьмём несколько кусочков цветного пластилина и склеим их, то потом всё же сможем разобрать, какие цвета были изначально, но если хорошенько перемешаем несколько баночек гуашевых красок, то точно восстановить исходные цвета без дополнительной информации уже будет невозможно.

(!) Важно понимать, когда мы берёмся анализировать реальный сигнал с помощью преобразования Фурье, мы идеализируем ситуацию и исходим из предположения, что он периодический на текущем временном интервале и состоит из элементарных синусоид. Зачастую это именно так, поскольку акустические сигналы, как правило, имеют гармоническую природу, но вообще возможны и более сложные случаи. Любые наши допущения о природе сигнала обычно ведут к частичным искажениям и погрешностям, но без этого выделить полезную информацию из него крайне сложно.

Теперь опишем весь процесс анализа более подробно:

1. Всё начинается с того, что звуковые волны колеблют мембрану микрофона, который преобразует их в аналоговые колебания электрического тока.

2. Затем происходит дискретизация аналогового электрического сигнала в цифровую форму. На этом моменте стоит остановиться подробно.

Поскольку аналоговый сигнал математически состоит из бесконечного непрерывного во времени множества точек-значений амплитуды, в процессе измерения мы можем выделить из него лишь конечный ряд значений в дискретные моменты времени, то есть, по сути, выполнить квантование по времени…

Как правило, значения-отсчёты берутся через небольшие равные временные промежутки, то есть с определённой частотой, например, 16000 или 22000 Гц. Однако в общем случае дискретные отсчёты могут идти и неравномерно, но это усложняет математический аппарат анализа, поэтому на практике обычно не применяется.

Существует важная теорема Котельникова-Найквиста-Шеннона, которая гласит, что аналоговый периодический сигнал, имеющий конечный (ограниченный по ширине) спектр, может быть однозначно восстановлен без искажений и потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте спектра (называемой частотой дискретизации или Найквиста).

Для этого восстановления необходимо применить специальные интерполирующие функции, но проблема в том, что при использовании данных функций вычисления нужно выполнять на бесконечном временном интервале, что на практике невозможно. Поэтому в реальной жизни нельзя сколь угодно повысить частоту дискретизации искусственным образом без искажений даже если изначально она удовлетворяет теореме Котельникова-Найквиста-Шеннона. Для этой операции применяются фильтры Фарроу.

Также дискретизация происходит не только по времени, но и по уровню значений амплитуды, поскольку компьютер способен манипулировать лишь ограниченным множеством чисел. Это также вносит небольшие погрешности.

3. На следующем этапе происходит само дискретное прямое преобразование Фурье.

Мы выделяем короткий кадр (интервал) композиции, состоящий из дискретных отсчётов, который условно считаем периодическим и применяем к нему преобразование Фурье. В результате преобразования получаем массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах анализируемого кадра. Причём спектры также являются дискретными с шагом равным (частота дискретизации)/(количество отсчётов). То есть чем больше мы берём отсчётов, тем более точное разрешение получаем по частоте. Однако при постоянной частоте дискретизации увеличивая число отсчётов, мы увеличиваем анализируемый временной интервал, а поскольку в реальных музыкальных произведениях ноты имеют различную длительность звучания и могут быстро сменять друг друга, происходит их наложение, поэтому амплитуда длительных нот «затмевает» собой амплитуду коротких. С другой стороны для гитарных тюнеров такой способ увеличения разрешения по частоте подходит хорошо, поскольку нота, как правило, звучит долго и одна.

Существует также довольно простой трюк для увеличения разрешения по частоте — нужно исходный дискретный сигнал заполнить нулями между отсчётами. Однако в результате такого заполнения сильно искажается фазовый спектр, но зато увеличивается разрешение амплитудного. Также возможно применение фильтров Фарроу и искусственное увеличение частоты дискретизации, однако и оно вносит искажения в спектры.

Длительность кадра обычно составляет приблизительно от 30 мс до 1 с. Чем он короче, тем лучшее разрешение мы получаем по времени, но худшее по частоте, чем сэмпл длиннее, тем лучшее по частоте, но худшее по времени. Это очень напоминает принцип неопределённости Гейзенберга из квантовой механики..и не с проста, как гласит Википедия, соотношение неопределенностей в квантовой механике в математическом смысле есть прямое следствие свойств преобразования Фурье…

Интересно и то, что в результате анализа сэмпла одиночного синусоидального сигнала амплитудный спектр очень напоминает дифракционную картинку…

Синусоидальный сигнал, ограниченный прямоугольным окном, и его «дифракция»

Дифракция световых волн

На практике это нежелательный эффект, затрудняющий анализ сигналов, поэтому его стараются понизить путём применения оконных функций. Таких функций придумано немало, ниже представлены реализации некоторых из них, а также сравнительное влияние на спектр одиночного синусоидального сигнала.

Применяется оконная функция ко входному кадру очень просто:

Что касается компьютеров, в своё время был разработан алгоритм быстрого преобразования Фурье, который минимизирует число математических операций, необходимых для его вычисления. Единственное требование алгоритма состоит в том, чтобы число отсчётов было кратно степени двойки (256, 512, 1024 и так далее).

Ниже его классическая рекурсивная реализация на языке C#.

Существует две разновидности алгоритма БПФ — с прореживанием по времени и по частоте, но оба дают идентичный результат. Функции принимают массив комплексных чисел, заполненный реальными значениями амплитуд сигнала во временной области, а после своего выполнения возвращают массив комплексных чисел, содержащий информацию об амплитудном и фазовом спектрах. Стоит помнить, что реальная и мнимая части комплексного числа — это далеко не то же самое, что его амплитуда и фаза!

magnitude = Math.Sqrt(x.Real*x.Real + x.Imaginary*x.Imaginary)
phase = Math.Atan2(x.Imaginary, x.Real)

Результирующий массив комплексных чисел заполнен полезной информацией ровно на половину, другая половина является лишь зеркальным отражением первой и спокойно может быть исключена из рассмотрения. Если вдуматься, то этот момент хорошо иллюстрирует теорему Котельникова-Найквиста-Шеннона, о том, что частота дискретизации должна быть не меньше максимальной удвоенной частоты сигнала…

Также существует разновидность алгоритма БПФ без рекурсии по Кули-Тьюки, которая часто применяется на практике, но она чуть более сложна для восприятия.

Сразу после вычисления преобразования Фурье удобно нормализовать амплитудный спектр:

Это приведёт к тому, что величина значений амплитуды получится одного порядка не зависимо от размеров сэмпла.

Вычислив амплитудный и частотный спектры, легко производить обработку сигнала, например, применять частотную фильтрацию или производить сжатие. По сути, таким образом можно сделать эквалайзер: выполнив прямое преобразование Фурье, легко увеличить или уменьшить амплитуду определённой области частот, после чего выполнить обратное преобразование Фурье (хотя работа настоящих эквалайзеров обычно основана на другом принципе — фазовом сдвиге сигнала). Да и сжать сигнал очень просто — нужно всего лишь сделать словарь, где ключом является частота, а значением соответствующее комплексное число. В словарь нужно занести лишь те частоты, амплитуда сигнала на которых превышает какой-то минимальный порог. Информация о «тихих» частотах, не слышимых ухом, будет потеряна, но получится ощутимое сжатие при сохранении приемлемого качества звучания. Отчасти этот принцип лежит в основе многих кодеков.

4. Точное определение частоты

Дискретное преобразование Фурье даёт нам дискретный спектр, где каждое значение амплитуды отстоит от соседних на равные промежутки по частоте. И если частота в сигнале кратна шагу равному (частота дискретизации)/(количество отсчётов), то мы получим выраженный остроконечный пик, но если частота сигнала лежит где-то между границами шага ближе к середине у нас выйдет пик со «срезанной» вершиной и нам будет затруднительно сказать, что же там за частота. Очень может быть что в сигнале присутствуют две частоты лежащие рядом друг с другом. В этом и заключается ограничение разрешения по частоте. Так же как на фотоснимке с низким разрешением мелкие предметы склеиваются и становятся неразличимы, так же и тонкие детали спектра могут теряться.

Но частоты музыкальных нот лежат далеко не на сетке шагов преобразования Фурье, а для повседневных задач настройки музыкальных инструментов и распознавания нот необходимо знать именно точную частоту. Более того, на низких октавах при разрешении от 1024 отсчётов и ниже сетка частот Фурье становится настолько редкой, что попросту на одном шаге начинают умещаться несколько нот и определить какая же на самом деле из них играет становится фактически невозможно.

Чтобы как-то обойти это ограничение иногда применяют аппроксимирующие функции, например, параболические.
www.ingelec.uns.edu.ar/pds2803/Materiales/Articulos/AnalisisFrecuencial/04205098.pdf
mgasior.web.cern.ch/mgasior/pap/biw2004_poster.pdf
Но всё это искусственные меры, которые улучшая одни показатели могут давать искажения в других.

Существует ли более естественный путь для точного определения частоты?
Да, и скрыт он как раз-таки в использовании фазового спектра сигнала, которым часто пренебрегают.
Данный метод уточнения частоты сигнала, основан на вычислении задержки фаз у спектров двух кадров, наложенных друг на друга, но немного сдвинутых во времени.

На C# реализация метода выглядит довольно просто:

Применение также несложное:

Обычно исходные кадры сдвинуты на 1/16 или 1/32 своей длины, то есть ShiftsPerFrame равно 16 или 32.

В результате мы получим словарь частота-амплитуда, где значения частот будут довольно близки к реальным. Однако «срезанные пики» всё ещё будут наблюдаться, хоть и менее выражено. Чтобы устранить этот недостаток, можно просто «дорисовать» их.

Нотный анализ музыкальных произведений открывает ряд интересных возможностей. Ведь имея в наличии готовый нотный рисунок, можно осуществлять поиск других музыкальных композиций со схожим рисунком.

Например, одно и то же произведение может быть исполнено на другом инструменте, в различной манере, с другим тембром, либо транспонировано по октавам, однако нотный рисунок останется похожим, что позволит найти различные варианты исполнения одного и того же произведения. Это очень напоминает игру «угадай мелодию».

В некоторых случаях подобный анализ поможет выявить плагиат в музыкальных произведениях. Также по нотному рисунку, теоретически, можно искать произведения определённого настроения или жанра, что поднимает поиск на новый уровень.

В этой статье изложены основные принципы точного определения частот акустических сигналов и выделения нот. А также показана некоторая тонкая интуитивная связь дискретного преобразования Фурье с квантовой физикой, что подталкивает на размышления о единой картине мира.

Источник