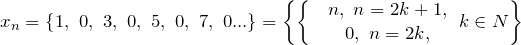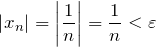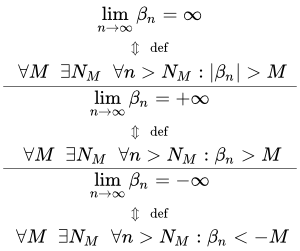Что такое бесконечно большая последовательность

Бесконечно малые и бесконечно большие последовательности

Бесконечно большие последовательности

Следствие. Любая бесконечно большая последовательность является неограниченной.

Замечание 2. Обратное утверждение в общем случае неверно.

является неограниченной, но не является бесконечно большой. Покажем это.

Бесконечно малые последовательности

Замечание 3. Любая бесконечно малая последовательность является ограниченной, но не наоборот.

Примеры решения задач

Задание	Доказать, что последовательность 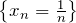является бесконечно малой.
Доказательство	Зададим произвольное положительное число и найдем такой номер 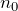элемента этой последовательности, что для всех выполняется соотношение

Что и требовалось доказать.

Источник

Определение бесконечно большой последовательности

Определение

Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.

Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.

Окрестности бесконечно удаленных точек

Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.

Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.

Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.

С помощью логических символов существования и всеобщности, это определение запишется так:
.

Примеры бесконечно больших последовательностей

Все примеры Сначала мы рассмотрим три простых похожих примера, а затем решим более сложный.

Пользуясь определением бесконечно большой последовательности показать, что
⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 2

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 3

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 4

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Бесконечно малая и бесконечно большая

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Содержание

Исчисление бесконечно малых и больших

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая величина

Последовательность называется бесконечно малой, если . Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки , если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то , .

Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция , неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки , если .

Функция называется бесконечно большой на бесконечности, если либо .

Свойства бесконечно малых

Сравнение бесконечно малых

Определения

Допустим, у нас есть бесконечно малые при одном и том же величины и (либо, что не важно для определения, бесконечно малые последовательности).

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения

Эквивалентные величины

Определение

Если , то бесконечно малые величины и называются эквивалентными ().

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

Теорема

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

Примеры использования

Исторический очерк

Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло. Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.

В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (положительной) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.

Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.

Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона). В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.

В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращённым названием «Аналист». Полное его название: «Аналист или рассуждение, обращённое к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры».

«Аналист» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин. И как вообще можно говорить об отношении между вещами, не имеющими величины. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии».

Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.

Как же с помощью анализа получаются правильные результаты? Беркли пришёл к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Как ни странно, некоторые крупные математики (например, Лагранж) согласились с ним.

Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.

В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс. В настоящее время термин «бесконечно малая» математики в подавляющем большинстве случаев относят не к числам, а к функциям или последовательностям.

Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.

Источник

Предел последовательности – основные теоремы и свойства

Определение последовательности

Более подробно см. страницу Определение числовой последовательности >>>.
Далее мы будем считать, что элементами последовательности являются действительные числа.

Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.

Определение предела последовательности

С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.

Свойства конечных пределов последовательностей

Основные свойства

Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.

Если последовательность имеет конечный предел, то она ограничена.

Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.

Арифметические действия с пределами

Свойства, связанные с неравенствами

Бесконечно большая и бесконечно малая последовательности

Бесконечно малая последовательность

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.

Бесконечно большая последовательность

Если последовательность бесконечно большая, а последовательность ограничена, то
.

Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.

Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.

Критерии сходимости последовательностей

Монотонные последовательности

Аналогичными неравенствами определяются другие монотонные последовательности.

Строго убывающая последовательность:
.
Неубывающая последовательность:
.
Невозрастающая последовательность:
.

Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.

Монотонная последовательность – это неубывающая или невозрастающая последовательность.

Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.

Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:

Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.

Критерий Коши сходимости последовательности

Фундаментальная последовательность – это последовательность, удовлетворяющая условию Коши.

Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.

Подпоследовательности

Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.

Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы после­довательностей>>>.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.

Источник

Бесконечно малые и бесконечно большие последовательности.

Бесконечно малые последовательности.

Последовательность \(\<\alpha_\>\) называется бесконечно малой, если
$$
\displaystyle \lim_\alpha_=0.\nonumber
$$

При изучении свойств сходящихся последовательностей нам потребуется ввести арифметические операции над последовательностями. Назовем суммой, разностью, произведением и частным двух последовательностей \(\\>\) и \(\\>\) соответственно последовательности \(\+y_\>\), \(\-y_\>\), \(\y_\>\), \(\/y_\>\). При определении частного предполагается, что \(y_n\neq 0\) для всех \(n\in\mathbb\).

Бесконечно малые последовательности обладают следующими свойствами:

Так как бесконечно малая последовательность ограничена, то из доказанного свойства следует, что произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Бесконечно большие последовательности.

Последовательность \(\\>\) называется бесконечно большой, если для любого \(\delta>0\) существует такой номер \(N_<\delta>\), что для всех \(n\geq N_<\delta>\) выполняется неравенство \(|x_|>\delta\). В этом случае пишут \(\displaystyle \lim_x_n=\infty\) и говорят, что последовательность имеет бесконечный предел.

Используя логические символы, это определение можно записать так:
$$
\displaystyle \ <\lim_x_=\infty\>\Leftrightarrow\forall\delta>0\ \exists N_<\delta>:\forall n\geq N_<\delta>\rightarrow|x_|>\delta.\label
$$
Дадим геометрическую интерпретацию определения \eqref. Назовем \(\delta\) — окрестностью \(\infty\) (рис. 5.1) множество \(E=\:|x|>\delta\>\). Если

Рис. 5.1

последовательность \(\\) имеет бесконечный предел, то в любой \(\delta\)-окрестности \(\infty\) лежат все члены последовательности, за исключением, быть может, конечного числа членов.

Аналогично вводятся для последовательности \(\\) понятия бесконечного предела, равного \(-\infty\) и \(+\infty\) Эти пределы обозначаются соответственно символами \(\undersetx_n=-\infty\) и определяются так:
$$
\<\undersetx_n=-\infty\>\Leftrightarrow\forall\delta>0 \ \exists N_<\delta>: \ \forall n\geq N_<\delta>\rightarrow x_ 0 \ \exists N_<\delta>: \ \forall n\geq N_<\delta>\rightarrow x_>\delta\label
$$

Множества \(E_1=\: \ x \delta\>\), где \(\delta > 0\), назовем \(\delta\)-окрестностями \(-\infty\) и \(+\infty\) соответственно (см. рис. 5.1). Тогда \(E=E_<1>\cup E_<2>\).

Согласно определению \eqref последовательность \(\\) имеет предел, равный \(+\infty\), если в \(\delta\)-окрестности символа \(+\infty\) содержатся все члены этой последовательности, за исключением, быть может, конечного числа их. Аналогичный смысл имеет определение \eqref.

В дальнейшем под пределом последовательности будем понимать конечный предел, если не оговорено противное.

Приведем примеры последовательностей, имеющих бесконечный предел:

Источник