Что такое бесконечная шкала
Шкала. Координатный луч
С помощью ровной деревянной рейки две точки A и B можно соединить отрезком (рис. 46 ). Однако этим примитивным инструментом измерить длину отрезка AB не удастся. Его можно усовершенствовать.
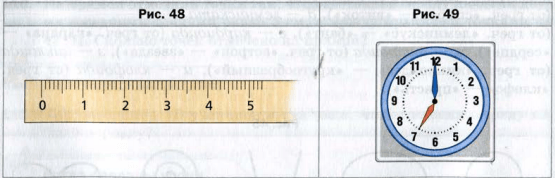
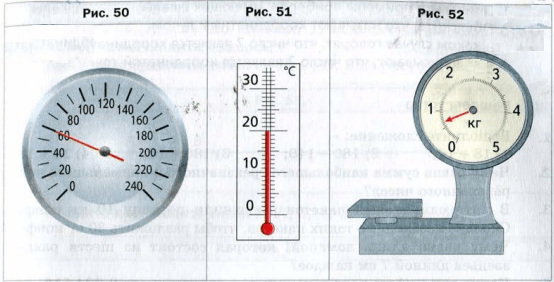
На рейке через каждый сантиметр нанесем штрихи. Под первым штрихом нанесем число 0, под вторым − 1, третьим − 2 и т.д. (рис. 47 ). В таких случаях говорят, что на рейку нанесена шкала с ценой деления 1 см. Эта рейка со школой похожа на линейку. Но чаще всего на линейку наносят шкалу с ценой деления 1 мм (рис. 48 ).
Из повседневной жизни Вам хорошо известны и другие измеритильные приборы, имеющие шкалы различной формы. Например: циферблат часов со шкалой деления 1 мин (рис. 49 ), спидометр автомобиля со шкалой деления 10 км/ч (рис. 50 ), комнатный термометр со шкалой деления 1 °C ( рис. 51 ), весы со шкалой деления 50 г (рис. 52 ).
Конструктор создает измерительные приборы, шкалы которых конечны, т. е. среди отмеченных на шкале чисел всегда есть наибольшее. А вот математик с помощью воображения может построить и бесконечную шкалу.
Начерти луч OX. Отметим на этом луче какую−нибудь точку E. Напишем над точкой O число 0, а под точкой E − число 1 (рис. 53 ).
Полученную бесконечную шкалу называют координатным лучом, точку O − началом отсчета, а отрезок OE − единичным отрезком координатного луча.
Виды шкал и их особенности
Проблема обеспечения высокого качества продукции тесным образом связана с проблемой качества измерений. Между ними явно прослеживается непосредственная связь: там, где качество измерений не соответствует требованиям технологического процесса, невозможно достичь высокого уровня качества продукции. Поэтому качество продукции в значительной степени зависит от успешного решения вопросов, связанных с точностью измерений параметров качества материалов и комплектующих изделий и поддержания заданных технологических режимов. Иными словами, технический контроль качества осуществляется путем замеров параметров технологических процессов, результаты измерений которых необходимы для регулирования процессом.
Следовательно, качество измерений представляет собой совокупность свойств состояния измерений, обеспечивающих результаты измерений с требуемыми точностными характеристиками, получаемые в необходимом виде за определенный отрезок времени.
Основные свойства состояния измерений:
• точность результатов измерений;
• воспроизводимость результатов измерений;
• сходимость результатов измерений;
• быстрота получения результатов;
При этом под воспроизводимостью результатов измерений понимается близость результатов измерений одной и той же величины, полученные в разных местах, разными методами, разными средствами, разными операторами, в разное время, однако в одних и тех же условиях измерений (температуре, давлении, влажности и т.д.).
Сходимость результатов измерений — это близость результатов измерений одной и той же величины, проведенных повторно с применением одних и тех же средств, одним и тем же методом в одинаковых условиях и с той же тщательностью.
Любое измерение или количественное оценивание чего-либо осуществляется, используя соответствующие шкалы.
Шкала — это упорядоченный ряд отметок, соответствующий соотношению последовательных значений измеряемых величин. Шкалой измерений называется принятая по соглашению последовательность значений одноименных величин различного размера.
В метрологии шкала измерений является средством адекватного сопоставления и определения численных значений отдельных свойств и качеств различных объектов. Практически используют пять видов шкал: шкалу наименований, шкалу порядка, шкалу интервалов, шкалу отношений и шкалу абсолютных значений.
Шкала наименований (номинальная шкала). Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов. Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше—меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка. Места, занимаемые величинами в шкале порядка, называются рангами, а сама шкала называется ранговой, или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше—меньше», «лучше—хуже» и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Шкала интервалов. Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам, температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.).
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10 до 20°С, то нельзя сказать, что стало в два раза теплее.
Шкала отношений. Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину объекта, мы узнаем, во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в данном случае) и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерения: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
Шкала абсолютных величин. Во многих случаях напрямую измеряется величина чего-либо. Например, непосредственно подсчитывается число дефектов в изделии, количество единиц произведенной продукции, сколько студентов присутствует на лекции, количество прожитых лет и т.д. и т.п. При таких измерениях на измерительной шкале отмечаются
абсолютные количественные значения измеряемого. Такая шкала абсолютных значений обладает и теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Результаты измерений по шкале абсолютных величин имеют наибольшую достоверность, информативность и чувствительность к неточностям измерений.
Шкалы интервалов, отношений и абсолютных величин называются метрическими, так как при их построении используются некоторые меры, т.е. размеры, принятые в качестве единиц измерений.
Шкала. Координатный луч
Урок 5. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Шкала. Координатный луч»
Представим себе такую историю.
– Интересно, что же у нас получится? – задумался Саша.
– Чем ты там занимаешься? – спросил Паша.
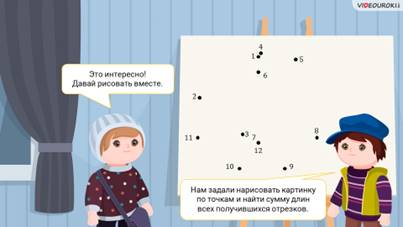
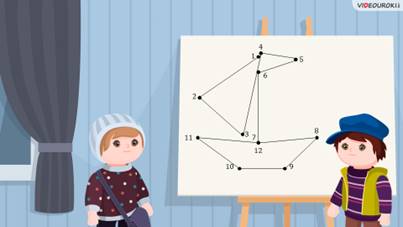
– Нам по математике задали нарисовать картинку по точкам, а потом найти сумму длин всех получившихся отрезков.
– Это интересно! Давай рисовать вместе.
– Давай! Вместе веселее.
И ребята принялись рисовать картинку.
– 1…, 2…, 3…, 4…, 5…, 6…, 7…, 8…, 9…, 10…, 11… и 12…
– Саша, смотри, у нас же получился корабль! – обрадовался Паша.
– Точно! – заметил Саша. Но нам ещё нужно вычислить сумму длин всех получившихся отрезков. Значит, будем мерить их линейкой.
– Саша, с твоей линейкой что-то не то! – отметил Паша. – Мы не сможем с помощью этой линейки измерить длины отрезков.
– Но у меня нет другой линейки. Как быть? – расстроился Саша.
– Я думаю, что Электроша будет знать, как нам быть, – предположил Паша.
– Ребята, прежде, чем я вам помогу с измерением отрезков, хочу, чтобы вы немного размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашей проблеме, – продолжил Электроша. – Вы не можете измерить длину отрезков, потому что на вашей линейке не хватает делений.
– Что значит не хватает делений? – удивился Саша. – На моей линейке же есть деления.
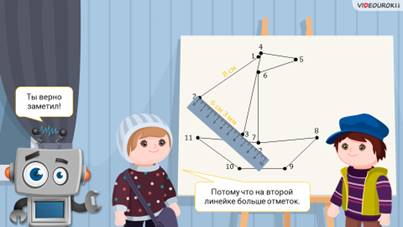
– Деления-то есть, – сказал Электроша, – но посмотрите, при измерении длины второго отрезка у вас не получилось записать его длину. Вы заметили, что он длиннее, чем 6 см, но точнее вам его измерить не удалось. Другое дело будет, если мы измерим длину этого же отрезка вот такой линейкой.
– Теперь понятно, про какие деления ты говорил, – обрадовались мальчишки.
– Посмотрите, отрезок один и тот же, а результаты измерения стали точнее, – продолжил Электроша. – Как вы думаете, почему так получилось?
– Наверное, потому что на второй линейке больше отметок, – предположил Паша.
– Ты верно заметил, – сказал Электроша.
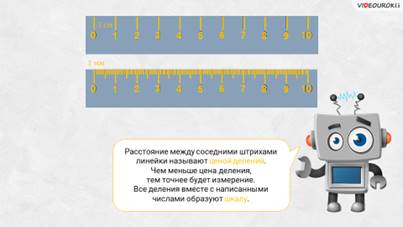
Давайте более внимательно рассмотрим эти две линейки. Посмотрите, на одной и второй линейке нанесены риски, штрихи. Все штрихи расположены на одинаковом расстоянии друг от друга. Около некоторых штрихов указаны числа. Нетрудно заметить, что все штрихи на линейках разбивают их на равные части. Эти части называют делениями.
– А теперь скажите, какое расстояние между соседними штрихами первой и второй линейки, – спросил у ребят Электроша.
– Расстояние между соседними штрихами первой линейки равно 1 см, а второй – 1 мм, – ответил Саша.
– Правильно! – подтвердил Электроша. Это расстояние называют ценой деления. Чем меньше цена деления, тем точнее будет измерение. Все деления вместе с написанными числами образуют шкалу.
Кстати, «шкала» по-латыни – это лестница.
– Тогда деления – это ступеньки лестницы? – спросил Паша.
– Точно подмечено, – ответил Электроша.
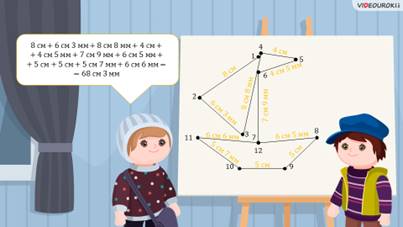
– С помощью второй линейки вы можете измерить длины отрезков вашего рисунка и найти их сумму.
– Да, теперь это гораздо легче выполнить, – сказал Паша. И ребята принялись измерять отрезки.
Получили, что сумма длин всех отрезков рисунка равна 68 см 3 мм.
– В повседневной жизни вы часто встречаетесь и с другими измерительными приборами, которые тоже имеют шкалы, правда, немного другой формы, – продолжил Электроша. Может, вы сможете их назвать? – спросил он у ребят.
– Комнатный термометр, – начал Паша, – циферблат часов.
– Спидометр автомобиля, – поддержал друга Саша, – весы.
– Молодцы! – похвалил ребят Электроша. А может, вы сможете назвать цены деления перечисленных измерительных приборов?
– У комнатного термометра цена деления – 1 о С, а вот у циферблата часов не знаю, как понять, какая цена деления, – расстроился Паша.
– У циферблата часов несколько шкал, каждая со своей ценой деления, – сказал Электроша. – Посмотрите, на циферблате вся окружность разделена на 12 больших делений. Одно деление соответствует одному часу. Кроме того, циферблат часов разделён на 60 маленьких делений. Одно такое маленькое деление соответствует одной минуте.
– Значит, у спидометра автомобиля цена деления шкалы 20 км/ч, а у весов цена деления 10 г? – решил уточнить Саша.
– Правильно! – похвалил Сашу Электроша. – А вы знаете, что измерительные приборы создают специально обученные люди, и их называют конструкторами? Правда, шкалы на таких измерительных приборах конечны, то есть среди отмеченных на шкале чисел всегда есть наибольшее. А вот математик с помощью своего воображения может построить бесконечную шкалу.
– Ого! – удивились ребята. – А ты можешь построить такую шкалу?
– Да! – ответил Электроша. – Сейчас мы её построим вместе.
Давайте начертим луч Ох так, чтобы он шёл слева направо. Отметим на этом луче, например, точку А. Теперь под точкой О поставим число 0, а под точкой А – число 1. Принято говорить, что точке О соответствует число 0, а точке А – число 1.
Обратите внимание, мы получили отрезок ОА, его длину будем считать равной 1.
Теперь отложим вправо от точки А отрезок, равный отрезку ОА. Получим новую точку, назовём её В, а под ней поставим число 2. Повторим этот шаг ещё раз. Получим ещё одну точку. Обозначим её буквой С, а под ней запишем число 3. Так, шаг за шагом, мы будем получать точки D, Е, F, которым будут соответствовать числа 4, 5, 6 и так далее.
– А сколько раз мы сможем проделывать эти шаги? – решили спросить ребята.
– Мы с вами знаем, что луч бесконечен, значит, мысленно этот процесс мы можем повторить бесконечное количество раз.
– Таким образом, мы с вами построили бесконечную шкалу.
– Ого! Так просто! – воскликнули ребята.
– Запомните! – продолжил Электроша. – Такую шкалу называют координатным лучом, точку О – началом отсчёта, а отрезок – ОА – единичным отрезком координатного луча. В качестве единичного отрезка можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на координатном луче необходимые натуральные числа.
– А вы сможете мне назвать то число, которое соответствует, например, точке G? – спросил у ребят Электроша.
– Число 7 соответствует точке G, – ответили мальчишки.
– Правильно! – сказал Электроша. Говорят, что число семь является координатой точки G, записывают это так…
Координата точки показывает расстояние от начала луча до этой точки, измеренное единичным отрезком. Так, например, на нашей координатной прямой точка Е имеет координату 5. Это говорит нам о том, что расстояние от начала координат до точки Е равно 5, или ещё можно сказать, что отрезок ОЕ имеет длину 5 единичных отрезков. Аналогично мы можем записать координаты остальных точек.
– А теперь, ребята, давайте посмотрим, как вы всё поняли и выполним несколько заданий.
Задание первое: назовите показания изображённых измерительных приборов.
Решение: на первом рисунке изображён комнатный термометр, который показывает температуру 31 о C. На втором рисунке изображены часы, на которых стрелки показывают время 12 ч 5 мин. И на последнем рисунке изображён спидометр автомобиля, на котором стрелка указывает скорость 90 км/ч.
Следующее задание: назовите координаты точек А, Бэ, Цэ, Дэ и отметьте на координатном луче точки.
Решение: сначала нам нужно назвать координаты точек, а для этого определим длину единичного отрезка. Видим, что от начала координат до первой известной координаты расстояние равное 30 и штрихами отмечено 3 единичных отрезка. Значит, длина единичного отрезка равна 10. А тогда координата точки А – 10, точки В – 50, точки С – 90, а точки D – 120.
Ещё нам нужно отметить на координатном луче точки с указанными координатами. Первая точка – F – имеет координату 20. Так как единичный отрезок равен 10, то отмечаем эту точку над вторым штрихом. Вторая точка – G – имеет координату 100, отмечаем её над десятым штрихом. И последняя точка – H – имеет координату 75. Значит, она будет располагаться между седьмым и восьмым штрихами.
Конспект уроков 1-3 по теме «Шкалы»
Обсуждение домашнего задания
К задаче 46 как провести вычисления количества отрезков, не строя сами отрезки
Задача1: даны 100 точек А1, А2, А100. Какое количество отрезков с концами в этих точках можно получить? Какое количество отрезков с началом в точке А4 можно получить?
Задача 2: даны цифры 6,3,4,5. Какое количество двузначных чисел можно получить (цифры могут повторяться)? А если цифры не могут повторяться?
. почему мы не делим на 2 кол-во вариантов
Каждый решает сам. Первый справившийся – к доске
Мы знаем и другие измерительные приборы: весы, часы, спидометр.
. А электронные весы являются измерительным прибором? А где их шкала? Какая цена деления?
Сушествуют ли еще измерительные приборы без шкалы?
Рассматривают рис 46-48, называют границы шкалы, цену деления
Рассматривают рис 49-52
На электронных весах нет шкалы и нет цены деления шкалы. Этот прибор Сам измеряет вес и выдает готовое значение. А шкала нужна, чтобы пользователь смотрел и определял вес сам.
В реальных измерительных приборах на шкале всегда есть наибольшее значение, выше которого измерить уже нельзя.
В математике, которая изучает плоскости и прямые, состоящие из бесконечного числа точек, существует своя, бесконечная шкала. Она похожа на бесконечно длинную линейку.
Сколько раз я так могу отложить, для скольки чисел получить соответствующую точку?
Полученную бесконечную шкалу называют координатным лучом, точку О, соответствующую числу 0 – началом отсчета, отрезок ОЕ, длину которого приняли за 1, единичным отрезком. Числа, соответствующие точкам на координатном луче, называются, координатами этих точек. Координаты точки записывают в круглых скобках.
Иногда точке не дают имя, а просо говорят «отметим число 6», т.е. отметим на координатном луче точку, координатой которой будет число 6.

Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 9