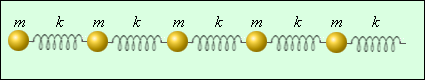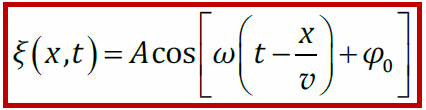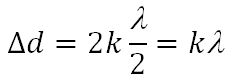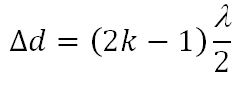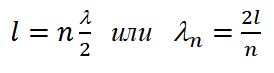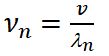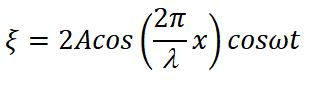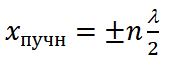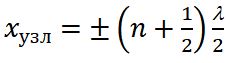Что такое бегущая волна и стоячая

Что такое стоячая волна? Что такое стоячая волна? Как она возникает? В чем отличие стоячей волны от бегущей?

Стоя́чая волна́ — колебания в распределенных колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

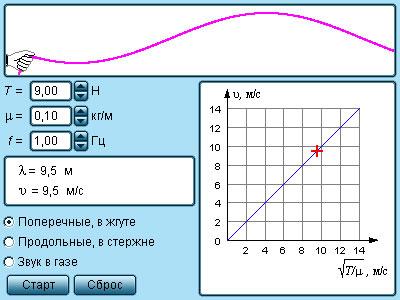
Для демонстрации стоячих волн в газе используют трубу Рубенса.

Всякий волновой процесс, связанный с распространением возмущений, может сопровождаться образованием С. в. Они могут возникать не только в газообразных, жидких и твёрдых средах, но также и в вакууме при распространении и отражении электромагнитных возмущений, например в электрических длинных линиях. Антенна радиопередатчика часто выполняется в виде прямолинейного вибратора или системы вибраторов, по длине которых устанавливается С. в. В отрезках волноводов и замкнутых объёмах различной формы, используемых в качестве резонаторов в технике сверхвысоких частот, устанавливаются С. в. определённых типов. В электромагнитных С. в. электрические и магнитные поля разделяются аналогично тому, как в упругих С. в. разделяются смещение и давление.

В оптике также возможно установление С. в. с видимыми максимумами и минимумами электрического поля. Если свет не монохроматический, то в С. в. пучности электрического поля разных длин волн будут расположены в разных местах и нередко наблюдается разделение цветов.

Налейте воды в ванну и пошлепайте рукой по поверхности. От руки будут разбегаться волны во все стороны. Они называются бегущие. Плавно изменяя частоту колебаний руки Вы можете добиться того, чтобы волны перестали перемещаться в стороны, а оставались на месте. Движение происходило бы только вверх и вниз. Это и есть стоячие волны.

Образуются они в данном случае только потому, что ванна имеет стенки, от которых происходит отражение, если бы стенок не было, то стоячие волны бы не образовались, как например, на открытой водной поверхности.

Объяснение возникновения стоячих волн простое, при сталкивании прямой волны и волны, отраженной от стенки, они усиливают друг друга, и если это сталкивание происходит все время в одном и том же месте, то исчезает горизонтальное перемещение волн.

Источник

Механические волны

Когда в каком-нибудь месте твердой, жидкой или газообразной среды происходит возбуждение колебаний частиц, результатом взаимодействия атомов и молекул среды становится передача колебаний от одной точки к другой с конечной скоростью.

Волна – это процесс распространения колебаний в среде.

Виды механических волн

Различают следующие виды механических волн:

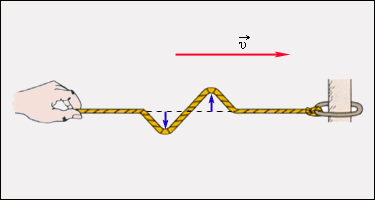
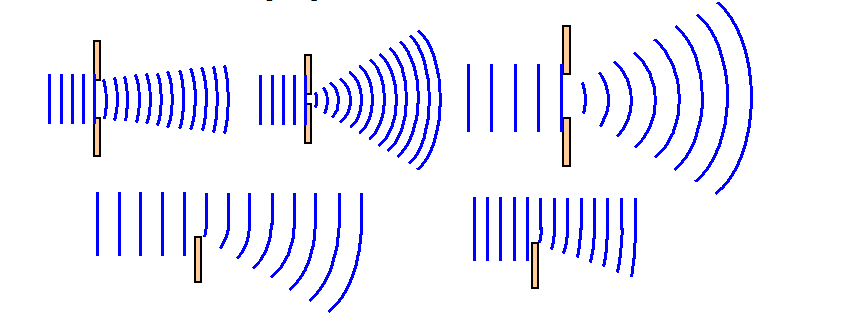
Поперечная волна: частицы среды смещаются в направлении, перпендикулярном направлению распространения механической волны.

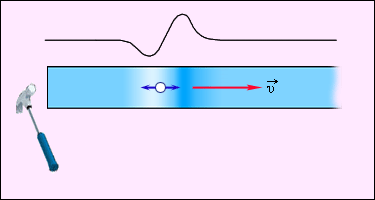
Продольная волна: частицы среды смещаются в направлении распространения механической волны.

Интересно, что волны на поверхности жидкости включают в себя и поперечную, и продольную компоненты.

Укажем важное уточнение: когда механические волны распространяются, они переносят энергию, форму, но не переносят массу, т.е. в обоих видах волн переноса вещества в направлении распространения волны не происходит. Распространяясь, частицы среды совершают колебания около положений равновесия. При этом, как мы уже сказали, волны переносят энергию, а именно энергию колебаний от одной точки среды к другой.

Модель твердого тела

Отличительная особенность продольных волн заключается в том, что они способны распространяться в любых средах: твердых, жидких и газообразных.

Если в указанной модели твердого тела один или несколько шариков получают смещение перпендикулярно всей цепочке, можно говорить о возникновении деформации сдвига. Пружины, получившие деформацию в результате смещения, будут стремиться вернуть смещенные частицы в положение равновесия, а на ближайшие несмещенные частицы начнет оказываться влияние упругих сил, стремящихся отклонить эти частицы от положения равновесия. Итогом станет возникновение поперечной волны в направлении вдоль цепочки.

В жидкой или газообразной среде упругая деформация сдвига не возникает. Смещение одного слоя жидкости или газа на некоторое расстояние относительно соседнего слоя не приведет к появлению касательных сил на границе между слоями. Силы, которые оказывают воздействие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. Аналогично можно сказать и о газообразной среде.

Таким образом, появление поперечных волн невозможно в жидкой или газообразной средах.

В приведенном выражении k = ω υ – так называемое волновое число, а ω = 2 π f является круговой частотой.

Бегущая волна

Из указанного выражения следует:

Из вышесказанного можно сделать вывод, что, когда бегущая волна получает распространение, появляется поток энергии, пропорциональный скорости волны и квадрату ее амплитуды.

Скорость распространения волны

Бегущие волны движутся в среде с определенными скоростями, находящимися в зависимости от типа волны, инертных и упругих свойств среды.

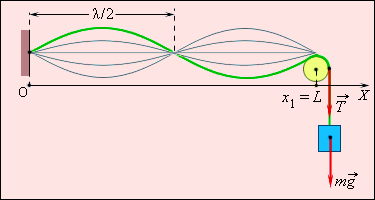
Скорость, с которой поперечные волны распространяются в натянутой струне или резиновом жгуте, имеет зависимость от погонной массы μ (или массы единицы длины) и силы натяжения T :

Таким образом, скорость распространения продольных волн в безграничной среде, определяется по формуле:

Если речь идет о продольных волнах, получающих распространение в упругих стержнях, запись формулы для скорости волны содержит не модуль всестороннего сжатия, а модуль Юнга:

Для стали отличие E от B незначительно, а вот для прочих материалов оно может составлять 20 – 30 % и больше.

Стоячая волна

Предположим, что механическая волна, получившая распространение в некоторой среде, встретила на пути некое препятствие: в этом случае характер ее поведения резко изменится. К примеру, на границе раздела двух сред с различающимися механическими свойствами волна частично отразится, а частично проникнет во вторую среду. Волна, пробегающая по резиновому жгуту или струне, отразится от зафиксированного конца, и возникнет встречная волна. Если у струны зафиксированы оба конца, появятся сложные колебания, являющиеся итогом наложения (суперпозиции) двух волн, получающих распространение в противоположных направлениях и испытывающих отражения и переотражения на концах. Так «работают» струны всех струнных музыкальных инструментов, зафиксированные с обоих концов. Схожий процесс возникает при звучании духовых инструментов, в частности, органных труб.

Если волны, распространяющиеся по струне во встречных направлениях, обладают синусоидальной формой, то при определенных условиях они образуют стоячую волну.

По струне одновременно пробегают в противоположных направлениях две волны с одинаковой частотой:

Приведенное выражение является описанием стоячей волны. Введем некоторые понятия, применимые к такому явлению как стоячая волна.

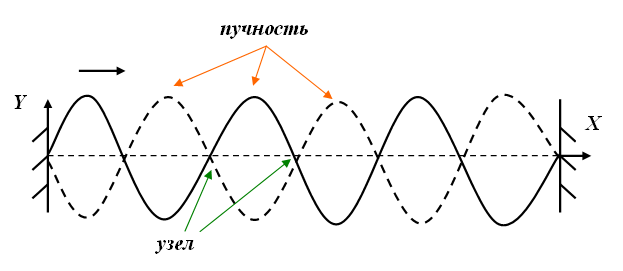
Узлы – точки неподвижности в стоячей волне.

Пучности – точки, расположенные между узлами и колеблющиеся с максимальной амплитудой.

Набору значений λ n длин волн соответствует набор возможных частот f

В этой записи υ = T μ есть скорость, с которой распространяются поперечные волны по струне.

Согласно принципу суперпозиции стоячие волны различных видов (с разными значениями n ) способны одновременно присутствовать в колебаниях струны.

Источник

Что такое бегущая волна и стоячая

Для существования волны необходим источник колебания и материальная среда или поле, в которых эта волна распространяется. Волны бывают самой разнообразной природы, но они подчиняются аналогичным закономерностям.

По физической природе различают:

упругие, звуковые, волны на поверхности жидкости

свет, радиоволны, излучения

По ориентации возмущений различают:

Смещение частиц происходит вдоль направления распространения;

могут распростаняться только в упругих средах;

необходимо наличие в среде силы упругости при сжатии;

могут распространяться в любых средах.

Смещение частиц происходит поперек направления распространения;

могут распростаняться только в упругих средах;

необходимо наличие в среде силы упругости при сдвиге;

могут распространяться только в твердых средах (и на границе двух сред).

Примеры: упругие волны в струне, волны на воде

По характеру зависимости от времени различают:

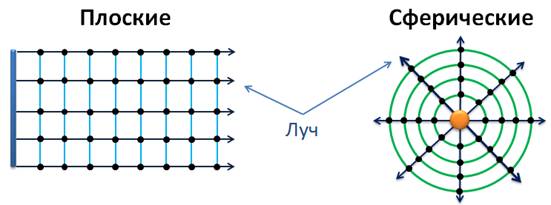
По форме волновой поверхности: плоская, сферическая, цилиндрическая волна.

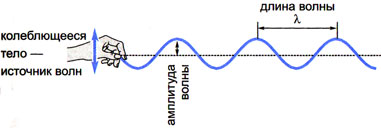
Характеристики волны

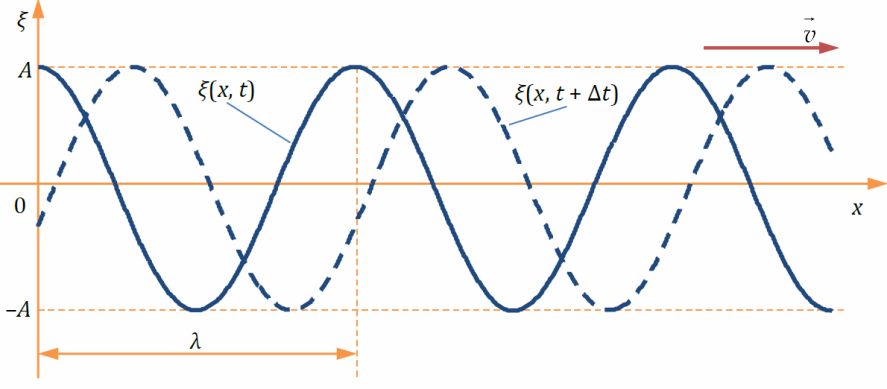
Уравнение бегущей волны

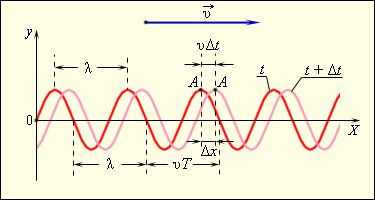
В процессе распространения бегущей волны возмущения среды доходят до следующих точек пространства, при этом волна переносит энергию и импульс, но не переносит вещество (частицы среды продолжают колебаться в том же месте пространства).

где v – скорость, φ₀ – начальная фаза, ω – циклическая частота, A – амплитуда

Свойства механических волн

1. Отражение волн – механические волны любого происхождения обладают способностью отражаться от границы раздела двух сред. Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду.

2. Преломление волн – при распространении механических волн можно наблюдать и явление преломления: изменение направления распространения механических волн при переходе из одной среды в другую.

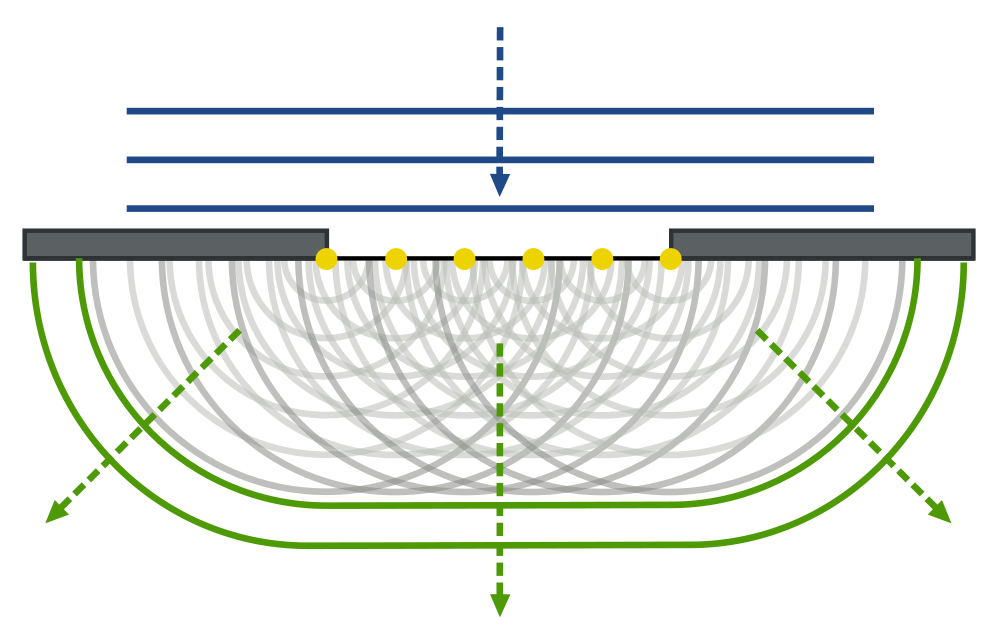
3. Дифракция волн – отклонение волн от прямолинейного распространения, то есть огибание ими препятствий.

4. Интерференция волн – сложение двух волн. В пространстве, где распространяются несколько волн, их интерференция приводит к возникновению областей с минимальным и максимальным значениями амплитуды колебаний

Интерференция и дифракция механических волн.

Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении.

При наложении волн может наблюдаться явление интерференции. Явление интерференции возникает при наложении когерентных волн.

Когерентными называют волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.

Интерференцией называется постоянное во времени явление взаимного усиления и ослабления колебаний в разных точках среды в результате наложения когерентных волн.

Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.

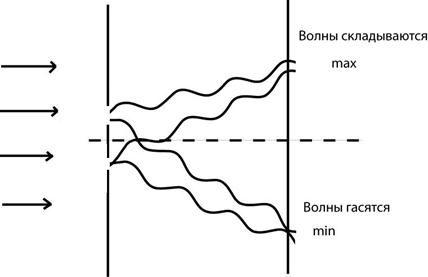
Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же – в противоположных фазах, то наблюдается ослабление колебаний. В результате в пространстве образуется устойчивая картина чередования областей усиленных и ослабленных колебаний.

Условия максимума и минимума

Если колебания точек А и Б совпадают по фазе и имеют равные амплитуды, то очевидно, что результирующее смещение в точке С зависит от разности хода двух волн.

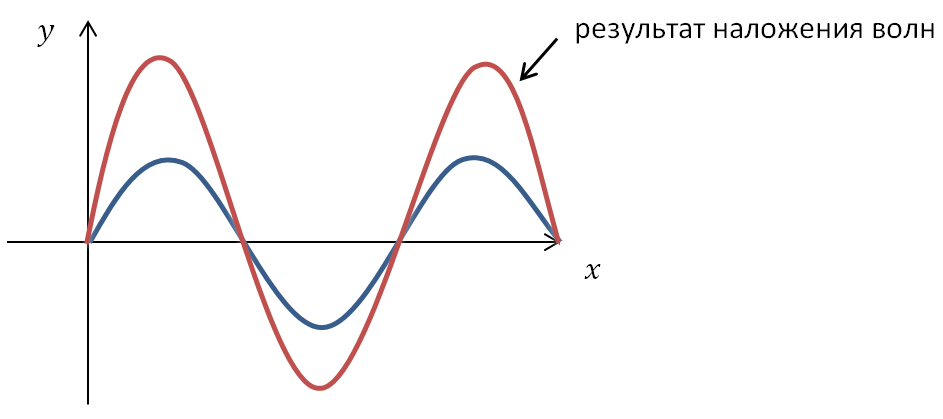
Условие максимума:

Амплитуда результирующего колебания А = 2x₀.

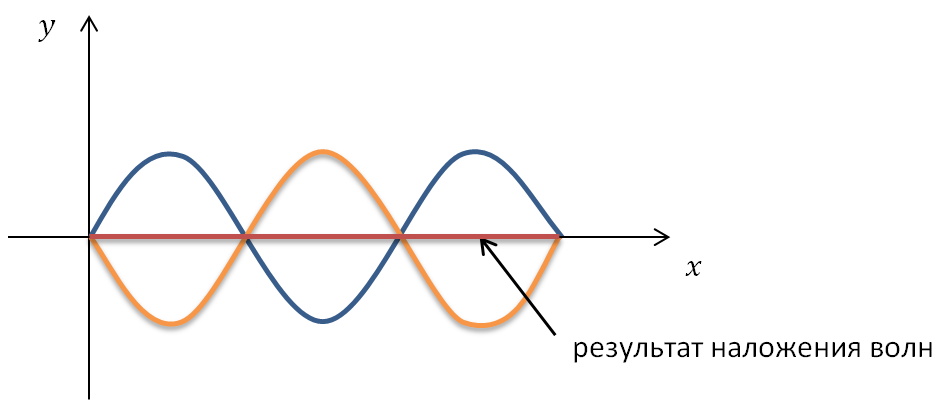
Если разность хода этих волн равна нечетному числу полуволн, то это означает, что волны от точек А и Б придут в точку С в противофазе и погасят друг друга.

Условие минимума:

Амплитуда результирующего колебания А = 0.

Если Δd не равно целому числу полуволн, то 0

Явление отклонения от прямолинейного распространения и огибание волнами препятствий называется дифракцией.

Соотношение между длиной волны (λ) и размерами препятствия (L) определяет поведение волны. Дифракция наиболее отчетливо проявляется, если длина набегающей волны больше размеров препятствия. Опыты показывают, что дифракция существует всегда, но становится заметной при условии d

Дифракция – общее свойство волн любой природы, которая происходит всегда, но условия её наблюдения разные.

Волна на поверхности воды распространяется в сторону достаточно большого препятствия, за которым образуется тень, т.е. волнового процесса не наблюдается. Такое свойство используется при устройстве волноломов в портах. Если же размеры препятствия сравнимы с длиной волны, то за препятствием будет наблюдаться волнение. Позади него волна распространяется так, как будто препятствия не было вовсе, т.е. наблюдается дифракция волны.

Примеры проявления дифракции. Слышимость громкого разговора за углом дома, звуки в лесу, волны на поверхности воды.

Стоячие волны

Стоячие волны образуются при сложении прямой и отраженной волны, если у них одинаковая частота и амплитуда.

В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.

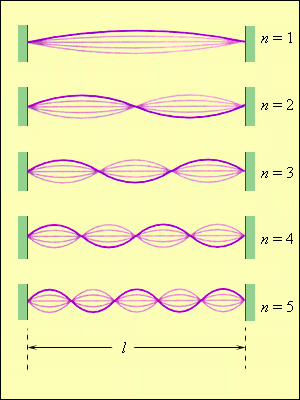
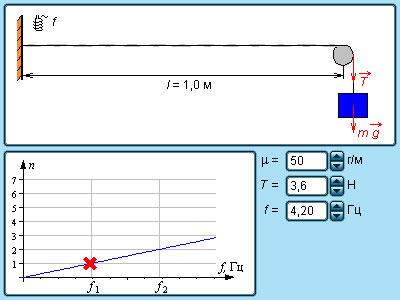
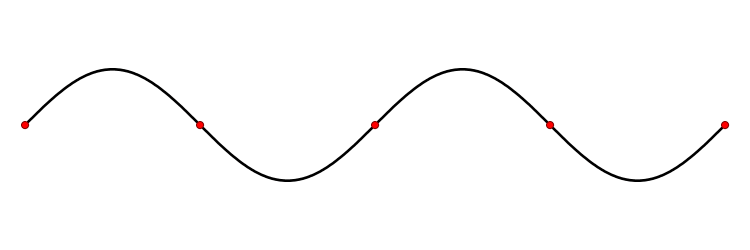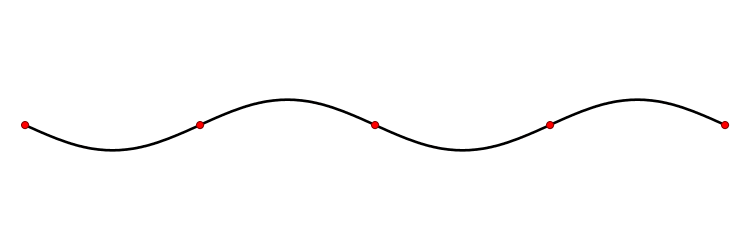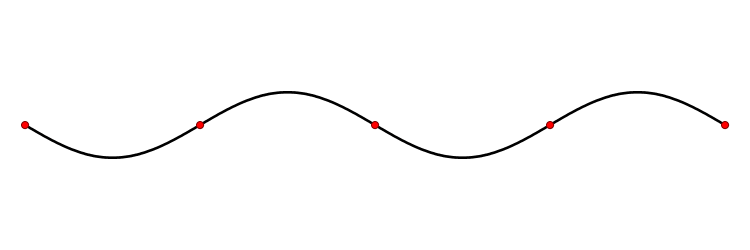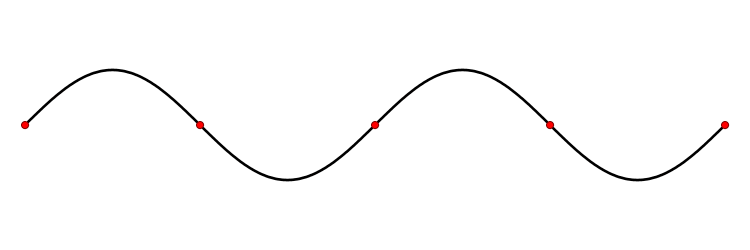
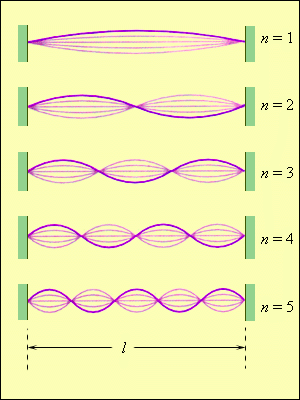
Колебания струны. В закрепленной с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причем в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.

Отсюда вытекает условие

Длинам волн соответствуют частоты

n = 1, 2, 3. Частоты v n называются собственными частотами струны.

Гармонические колебания с частотами v n называются собственными или нормальными колебаниями. Их называют также гармониками. В общем случае колебание струны представляет собой наложение различных гармоник.

Уравнение стоячей волны:

В точках, где координаты удовлетворяют условию 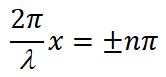(n = 1, 2, 3, …), суммарная амплитуда равна максимальному значению – это пучности стоячей волны. Координаты пучностей:

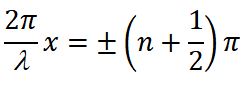
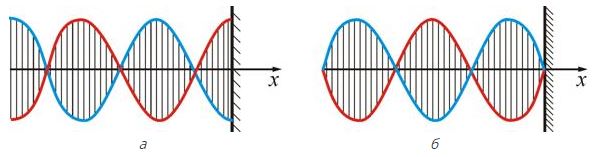
В точках, координаты которых удовлетворяют условию (n = 0, 1, 2,…), суммарная амплитуда колебаний равна нулю – это узлы стоячей волны. Координаты узлов:

Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (a), и узел – если более плотная (б).

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.

Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.

Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.

Источник

Что такое бегущая волна и стоячая

ВОЛНОВОЕ ДВИЖЕНИЕ 2 — БЕГУЩИЕ И СТОЯЧИЕ ВОЛНЫ

Бегущими называются волны, которые распространяются в пространстве или среде. У механических волн частицы вдоль направления распространения волны перемещаются на максимальное расстояние от точки равновесия при прохождении через нее гребня или впадины волны. Частицы, разделенные целым числом длины волны, колеблются в одной фазе друг с другом.

Стоячие волны образуются в результате наложения двух или более бегущих волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды. Амплитуда результирующей волны изменяется в зависимости от положения точки. Точки, в которых амплитуда минимальна, называются узлами, а в которых амплитуда максимальна — пучностями. Узлы образуются, так как бегущие волны в данной точке различаются на полфазы и здесь же компенсируют друг друга. Расстояние между смежными узлами всегда равно половине длины волны.

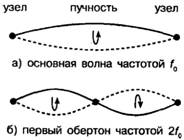
Стоячие волны могут образоваться на колеблющейся струне с узлом на каждом конце. При таком колебании длина струны измеряется целым числом половин длины волны. Если длина колеблющейся струны равна одной половине длины волны, то такая волна называется основной.

Стоячие волны образуются в столбе воздуха внутри трубы органа, резонирующего и издающего звук. Струя воздуха, проходящая сквозь щель, заставляет воздушный столб вибрировать и распространяет звуковые волны вдоль трубы. Внутри ее некоторые из этих звуковых волн отражаются в конце столба и идут навстречу друг другу, образуя чередующиеся узлы и пучности вдоль всего столба.

Стоячие волны струны

Стоячие волны струны

См. также статьи «Волновое движение 1», «Интерференция».

Источник

Бегущие и стоячие волны

В течение длительного времени явления, связанные с бегущими волнами, были сферой интереса только инженеров, работавших в области телекоммуникаций и передачи электроэнергии на большие расстояния. Однако с развитием техники управления электродвигателями с использованием широтно-импульсной модуляции (ШИМ), а также с увеличением рабочих частот этой модуляции даже в цепях электродвигателей стали проявляться эффекты стоячих волн. Понимание явлений, связанных с бегущими волнами в передающих линиях, стало необходимым, например, для защиты электродвигателей, питание которых осуществляется через длинную кабельную линию и (или) на высокой частоте. Если говорить современными терминами, передающая линия — это набор нескольких параллельных или коаксиальных проводников конечной длины, будь то проводники на печатной плате или многомильная линия электропередачи.

Появление стоячих волн наблюдается в тех случаях, когда физическая протяженность передающей линии сопоставима с длиной электрической волны в ней. В свою очередь длина волны зависит от частоты ее возбуждения. Образуются стоячие волны вследствие интерференции между падающими на нагрузку и отраженными от нее волнами. Поведение волн в линии может быть определено решением системы дифференциальных уравнений, в которые входят параметры линии и частота ее возбуждения. Решение этих уравнений с учетом потерь весьма сложно и мало дает с практической точки зрения, поэтому мы ограничимся анализом линий без потерь.

Дифференцируя их по x, а затем по t, мы получим отдельные дифференциальные эллиптические уравнения второго порядка для e и i как функции от t и x. Их классическая форма:

LCd 2 i/dt 2 — 8 2 i/8x 2 = 0 и LCd 2 e/dt l — д 2 е/дх 2 = 0.

Эти уравнения могут быть решены методом преобразования или классическим методом. Их решения получаются в форме гиперболических функций на комплексной плоскости и до развития компьютерной техники были единственным практическим средством анализа передающих линий. К счастью, компьютеры позволяют использовать числовые методы анализа, и при этом даже потери могут быть учтены сравнительно легко. С применением интеграции по Эйлеру процесс решения дифференциальных уравнений сейчас не так страшен, как раньше.

На Рис. 6.1 приведены разностные уравнения для отдельных участков передающей линии. Эти уравнения при решении их численными методами позволяют получить значения напряжений и токов в линии как функции расстояния и времени. Хотя сразу это и неочевидно, эти уравнения в пределе повторяют дифференциальные уравнения, которые мы рассмотрели выше.

Рис. 6.1. Разностные уравнения для отделъныхучастков передающей линии

Воздушная линия электропередачи с расстоянием между проводами 6 футов:

Экранированный коаксиальный кабель на 15 кВ, с центральным проводником площадью сечения 500 kcm:

(Скорости распространения показаны в процентах от скорости света, равной 310 8 м/с.)

Воздушная линия электропередачи имеет высокое значение последовательной индуктивности и сравнительно низкое значение емкости, так что характеристическое сопротивление оказывается довольно большим. В этой линии скорость распространения сравнительно большая, что обусловлено малыми значениями емкостей. В кабельной линии все наоборот. Экранированный кабель имеет очень большую емкость, что делает его характеристическое сопротивление малым, как и скорость распространения. Отметим, что в кабельной линии длина волны составляет менее чем одну треть от длины волны на данной частоте в открытом пространстве.

Явления, связанные с переходными процессами

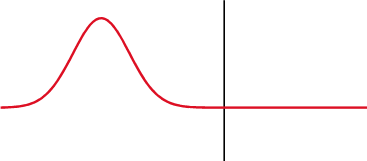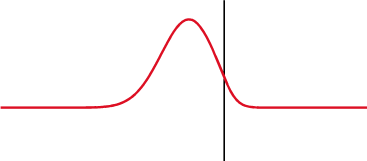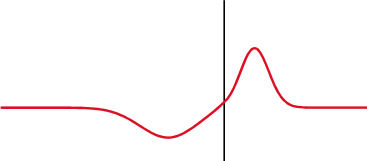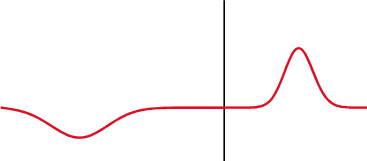
Проблемы, которые могут возникать в цепях электродвигателей из-за бегущих волн, могут быть проиллюстрированы результатами изучения отклика линии на бросок напряжения. На Рис. 6.2 показан предельный случай, когда импеданс генератора в передающей линии принят равным нулю, а нагрузка не подсоединена. Коэффициент отражения RC определяется выражением RC = (Z_T Z₀)/(Z_X + Z₀), где Z_T — импеданс нагрузки, а Z₀ — импеданс генератора. В отсутствие нагрузки RC = 1.

Когда бегущая волна достигает конца линии, возникает отраженная волна. Если коэффициент отражения RC имеет положительное значение, то отраженная волна складывается с падающей по амплитуде. Если коэффициент отражения отрицательный, то отраженная волна вычитается из падающей. В предельных случаях при разомкнутой цепи нагрузки напряжение на выходе линии удваивается, а при коротком замыкании становится равным нулю. При этом’в обоих случаях отраженная волна движется в направлении от конца линии к генератору, а падающая — от генератора к концу линии. Этот процесс показан на Рис. 6.2 при единичном значении скачка приложенного к линии напряжения. В каждой точке линии напряжение является суммой падающей и отраженной волн.

Рис. 6.2. Отражение в передающей линии при отсутствии нагрузки

На приемном конце линии напряжение будет изменяться в соответствии с последовательностью +2, +2, 0, 0, +2… до тех пор, пока напряжение приложено к передающему концу. Передающий конец линии будет отражать с переворотом полярности падающую на него волну, а приемный — отражать с той же полярностью. Хотя в этом примере мы рассматривали линию без потерь, с чистыми отражениями, в экранированных кабелях и других достаточно длинных линиях передачи процессы практически те же самые.

На Рис. 6.3 показано поведение импульсов напряжения единичной амплитуды при прохождении их через передающую линию при различной крутизне их фронтов. Отметим, что при продолжительности фронтов, в десять и более раз превышающей время распространения по линии (в данном примере 2 мкс), эффект возрастания амплитуды напряжения из-за сложения падающих и отраженных импульсов практически полностью исчезает. Подобная коррекция формы импульсов напряжения может быть выполнена с помощью фильтра нижних частот на передающем конце линии для защиты оборудования на приемном конце линии.

На Рис. 6.4 приведен график зависимости перенапряжения на приемном конце линии от относительной длительности фронтов импульсов.

Теоретически при периодических сигналах на передающем конце линии не существует ограничений на рост амплитуды напряжения на ее приемном конце. На практике потери в линии ограничивают это напряжение, но оно все равно может разогнаться до намного больших значений, чем при одиночном импульсе.

Способы уменьшения перенапряжения

Для уменьшения бросков напряжения на нагрузке следует уменьшать крутизну фронтов импульсов на передающем или приемном концах линии передачи. В принципе можно было бы согласовать импедансы линии и нагрузки, но на практике это редко возможно из-за отсутствия информации о высокочастотных характеристиках нагрузки. Обычно ограничиваются установкой на входе передающего конца линии фильтра нижних частот или дросселя. При использовании дросселя его индуктивность выбирают в 5 раз больше, чем индуктивность линии. Для исключения проблем, связанных с резонансными явлениями, при расчете фильтра нижних частот полезно провести компьютерное моделирование цепи и процессов в ней.

Рис. 6.3. Влияние длительности фронтов импульсов с выхода генератора на форму напряжения на приемном конце линии, состоящей из экранированного кабеля 500’ 2/0 15 кВ

Рис. 6.4. Зависимость перенапряжения на приемном конце линии от относительной длительности фронтов импульсов

Если выводы электродвигателя, используемого в качестве нагрузки, доступны, то полезно бывает зашунтировать их конденсатором, подавляющим броски напряжения. Однако для исключения резонансных явлений может потребоваться последовательно с конденсатором включить резистор, и опять пригодится компьютерное моделирование.

Источник: Сукер К. Силовая электроника. Руководство разработчика. — М.: Издательский дом «Додэка-ХХI, 2008. — 252 c.: ил. (Серия «Силовая электроника»).

Источник