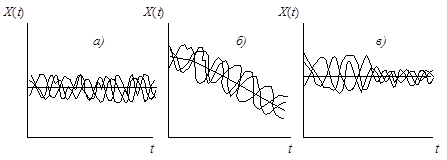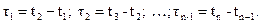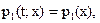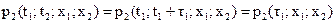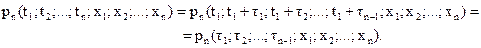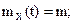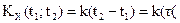Для стационарного процесса в узком смысле не может быть того что

Стационарные случайные процессы

К числу наиболее простых для изучения случайных процессов относятся стационарные случайные процессы у которых все вероятностные характеристики не зависят от времени. В частности, у стационарного случайного процесса математическое ожидание и дисперсия из функций аргумента t превращаются в константы:

, (6.20)

. (6.21)

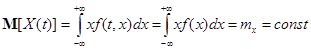
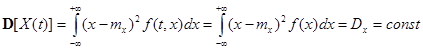
Это означает, что все сечения стационарного случайного процесса имеют одинаковое математическое ожидание и дисперсию (рис.6.4).

Рис.6.4. Реализации стационарного (а) и нестационарных (б,в) случайных процессов; б – нестационарность по математическому ожиданию; в – нестационарность по дисперсии.

Различают стационарные случайные процессы в узком смысле и в широком смысле.

Случайный процесс называется стационарным в узком смысле, если его n-мерная плотность распределения не изменится при сдвиге всех его временных аргументов на одинаковую произвольную величину q.

Поясним это на примере двумерной плотности распределения. Если стационарный случайный процесс X(t) имеет двумерную плотность f(t₁, t₂, x₁, x₂), то она не изменится если заменить t₁ на t₁+ q, а t₂на t₂ +q.

Это означает, что плотность распределения стационарного случайного процесса не зависит от того в какие моменты t₁ и t₂ рассматриваются сечения, а зависит от расстояния между этими сечениями t₁ – t₂ = t.

Случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно (m_x = conct), а корреляционная функция – есть функция сдвига между аргументами: K_x(t₁, t₂) = k_x(t).

Если стационарный случайный процесс является стационарным в узком смысле, то он является стационарным и в широком смысле (обратное утверждение не всегда верно).

Корреляционная функция стационарного случайного процесса обладает следующими свойствами:

1. Она является четной функцией своего аргумента

. (6.22)

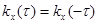
2. Значение корреляционной функции стационарного случайного процесса при нулевом сдвиге t равно дисперсии случайного процесса

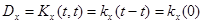
. (6.23)

3. . (6.24)

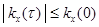
Помимо корреляционной функции используется нормированная корреляционная функция стационарного случайного процесса, которую также называю автокорреляционной функцией:

. (6.25)

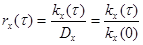
Она обладает практически теми же свойствами, что и корреляционная функция, у которой изменен масштаб по оси ординат:

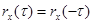
1. . (6.26)

2. . (6.27)

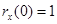
3. . (6.28)

Источник

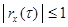
Понятие стационарного случайного процесса. Стационарность в узком и широком смыслах

Стационарным (однородным во времени) называют случайный процесс, статистические характеристики которого не меняются с течением времени, то есть являются инвариантными относительно временных сдвигов.

Различают случайные процессы стационарные в широком и узком смысле.

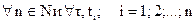
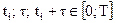
Стационарным случайным процессом в узком смысле называется случайный процесс Х(t), все вероятностные характеристики которого не меняются со временем, то есть таких, что выполняется условие

F(t₁; t₂;… ;t_n; x₁; x₂;…; x_n)=F(t₁+τ; t₂+τ;… ;t_n+τ; x₁; x₂;…; x_n), и, следовательно, все n-мерные распределения зависят не от моментов времени t₁; t₂;… ;t_n, а от длительности временных промежутков τ_i:

В частности, одномерная плотность распределения вообще не зависит от времени t:

двумерная плотность сечений в моменты времени t₁ и t₂

n-мерная плотность сечений в моменты времени t₁; t₂. ; t_n:

Случайный процесс Х(t) называется стационарным в широком смысле, если его моменты первого и второго порядка инвариантны относительно временного сдвига, то есть его математическое ожидание не зависит от времени t и является константой, а корреляционная функция зависит только от длины временного промежутка между сечениями:

Очевидно, что стационарный случайный процесс в узком смысле является стационарным случайным процессом и в широком смысле; обратное утверждение не верно.

Дата добавления: 2015-07-30 ; просмотров: 4209 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

ОТветы на синергию. Эконометрика. Автокорреляционная функция это функция от Тип ответа

Модель авторегрессии первого порядка

Обобщенный метод наименьших квадратов

Постоянство дисперсии случайного члена регрессионного уравнения

Отсутствие зависимости между остатками текущих и предыдущих наблюдений

Процесс не является стационарным в широком смысле

Показатель, характеризующий тесноту линейной стохастической связи между переменными

Явление линейной стохастической связи между переменными

Показатель, позволяющий установить факт наличия линейной

стохастической связи между переменными

Дисперсии зависимой переменной, объясняемую регрессией в общей ее дисперсии

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Статистической значимости модели в целом

Статической зависимости каждого из коэффициентов модели

Определения статической значимости каждого коэффициента уравнения

Наличие линейной зависимости между несколькими объясняющими переменными

Дисперсии коэффициентов регрессии

Числа структурных коэффициентов над числом приведенных

О мультиколлинеарности факторов

Значение коэффициента равно нулю

С ростом Х происходит убывание У

Объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной

Ранговое условие и порядковое условие со знаком равенства

Коэффициенты множественной детерминации некоторых объясняющих факторов с остальными

Переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии

Положительные и отрицательные

Эндогенных переменных минус единица

Отбор факторов, влияющих на результат и выбор вида уравнения

Парные и множественные

Необходимым и достаточным

Системы минус единица

Процентное изменение зависимой переменной при однопроцентном изменении независимой переменной

Проверки статистической значимости фактора

Можно рассматривать в узком и в широком смысле

Характеристика временного ряда, связанная с его стабильностью

Качество уровня регрессии в целом

По нормальному закону

Качество уравнения регрессии в целом

Ее математическое ожидание не равно ей

Связь между переменными, сложенная влиянием случайных факторов

Обладают свойством гетероскедастичности

Источник