Для чего в физике вводят модельные приближения физика 10

Физика и познание мира (продолжение)

Модели в физике

Одним из мощных методов исследования в физике является метод моделирования.

Запомни
Моделирование — это процесс замены реального объекта, процесса или явления другим, называемым моделью.
Модель — это идеализация реального объекта или явления при сохранении основных свойств, определяющих данный объект или явление.

Подчеркнём, что модель должна сохранять те свойства реального объекта, которые определяют его поведение. Модели бывают теоретическими и лабораторными, в последнее время широко используются компьютерные модели.

При создании теоретической модели используются результаты наблюдений и экспериментов. Очевидно, что проблема становится более понятной с помощью конкретных образов, именно поэтому модель чаще всего бывает механической. Например, движение молекул газа наглядно можно представить как движение упругих шариков, строение атома сначала предполагалось аналогичным строению Солнечной системы.

Одна из первых моделей, которой мы будем пользоваться, — это материальная точка, т. е. тело, размерами и формой которого можно пренебречь в условиях данной задачи. Последние слова являются ключевыми: именно условия конкретной задачи позволяют применить данную модель.

Сначала, когда данных мало, модель, как правило, получается грубой, но по мере накопления экспериментальных фактов она уточняется, однако для ответов на некоторые важные вопросы можно остановиться и на примитивной модели.

В лаборатории моделируются, как правило, явления, изучение которых в природных условиях представляет значительные трудности. Например, течение реки, изменение её русла моделируются в гидравлических лотках, испытание моделей самолётов проводится в аэродинамической трубе. При этом должны выполняться разные условия подобия — геометрическое, кинематическое и т. д.

Теоретическое решение любой физической задачи сводится к математическому моделированию, т. е. написанию уравнений. Часто эти уравнения получаются достаточно сложными, и их решения делаются с помощью компьютеров.

Научные гипотезы

Запомни
Научная гипотеза — высказанное суждение, недоказанное утверждение, предположение, объясняющие наблюдаемые явления или результаты лабораторных экспериментов.

Научная гипотеза всегда выдвигается для решения конкретной проблемы, чтобы объяснить полученные экспериментальные данные или устранить разногласия между теоретическими и экспериментальными результатами, полученными в ходе проверки ранее выдвинутых гипотез. Например, немецкий физик-теоретик, основоположник квантовой теории, М. Планк, разрабатывая квантовую гипотезу, опирался как на выводы, полученные в рамках классической теории излучения, так и на отрицательные результаты проверки предыдущих гипотез.

Слова русского учёного Д. И. Менделеева подтверждают важность научных гипотез в процессе научного познания: «Они (гипотезы. — Авт.) науке и особенно её изучению необходимы. Они дают стройность и простоту, каких без их допущения достичь трудно. Вся история наук это показывает. А потому можно смело сказать: лучше держаться такой гипотезы, которая может оказаться со временем неверною, чем никакой. Гипотезы облегчают и делают правильною научную работу — отыскание истины, как плуг земледельца облегчает выращивание полезных растений».

Физические величины и их измерение

Для того чтобы понять и описать эксперименты, учёные вводят целый ряд физических величин, таких, как скорость, сила, давление, температура, электрический заряд и многие другие. Каждой величине надо дать точное определение, ввести её наименование в определённой системе единиц, указать, как эту величину можно измерить, как провести необходимый для такого измерения опыт.

Чаще всего в определениях физических величин просто уточняют и придают количественную форму тому, что непосредственно воспринимается нашими органами чувств. Так вводят понятия силы, температуры и т. д. Есть, конечно, величины, которые не воспринимаются непосредственно нашими органами чувств (например, электрический заряд). Но они выражаются через другие величины, на которые органы чувств человека реагируют. Так, электрический заряд определяется по силам взаимодействия между заряженными телами.

Для измерения физической величины необходим эталон, стандарт, т. е. некоторое средство измерения, позволяющее хранить единицу, передавать и повторять её размер. Эталоны, такие, например, как эталоны метра, килограмма и многих других величин, хранятся в Международном бюро мер и весов в Севре (Франция). Точные копии эталона разосланы в разные лаборатории мира.

А существует ли вообще точное значение физической величины? Мы знаем, что любое тело состоит из атомов. При увеличении точности измерения мы приходим к необходимости измерения объектов очень малых размеров, таких, как атомы и молекулы. Одним из существенных выводов квантовой механики был вывод о том, что бессмысленно даже ставить вопрос о точном значении физической величины, причём неопределённость лежит в основе самих законов природы, а не в несовершенстве приборов.

Источник

Физические модели

Всего получено оценок: 275.

Всего получено оценок: 275.

Физика изучает самые общие свойства Природы, устанавливая правила и законы, по которым происходят всевозможные процессы и явления. При этом практически всегда используется прием, называемый физическим моделированием. Рассмотрим суть этого приема подробнее, дадим определение физической модели.

Необходимость упрощения

Рассматривая любое физическое явление, можно всегда заметить, что среди множества характеристик реального объекта существуют как важные для текущей практической задачи, так и второстепенные, не влияющие на нее.

Рис. 1. Явления, изучаемые физикой.

Например, если стоит практическая задача взвешивания груза, она решается с помощью весов, которые могут иметь самые различные принципы и конструкции. Точное описание процесса, происходящего при простейшем взвешивании, может включать огромное количество всевозможных характеристик и закономерностей, начиная от макроскопических (например, форму, которую имеют весы), и заканчивая микроскопическими (например, точным химическим составом частей весов).

Однако, для поставленной задачи большая часть этих параметров являются несущественными. Решение задачи требует, чтобы взвешиваемая масса была равна заданной (это важный параметр в данном случае), а какую форму имеют весы, и каков точный химический состав сплава, из которого они сделаны – для решения не играет роли (это второстепенные и неважные параметры).

Точно так же, в любом физическом процессе и явлении можно выделить огромное множество характеристик, но важными для поставленной задачи будут являться далеко не все. И при физическом описании разумно всегда использовать минимум необходимых параметров.

Здесь действует важная философская концепция, называемая «Бритвой Оккама». Она гласит, что из всех теорий, правильно описывающих явление, следует отдавать предпочтение более простой.

Физическая модель

Применение принципа упрощения наиболее ярко проявляется в использовании специальных объектов, называемых «физическими моделями».

Физическая модель – это некоторое описание реального явления, в котором участвует минимум параметров, необходимых для правильного описания явления и правильного решения поставленных задач.

Хорошим примером физической модели является понятие «материальной точки». Данное понятие используется в механике для описания движения и взаимодействия тел. Материальная точка имеет некоторые координаты в выбранной Системе Отсчета и некоторую массу. При этом, как и геометрическая точка, она не имеет ни формы, ни объема, ни ориентации в пространстве. Все понимают, что в Природе нет объектов, которые бы не имели формы, объема и ориентации, но при этом еще бы и имели некоторую массу. Однако, для описания движения и взаимодействия тел во многих случаях все эти характеристики реальных тел неважны. В кинематике изучается только движение и координаты тела. В динамике и статике также важна масса тела. Остальные параметры для законов движения практически всегда не важны.

В итоге в механике модель «материальная точка» используется в большинстве случаев.

В других областях физики используются другие модели. Например, в термодинамике такой моделью является идеальный газ. В электродинамике – идеальные проводники и диэлектрики. В оптике – абсолютно черное тело.

Рис. 3. Физические модели.

Что мы узнали?

В описании любого физического явления существуют важные и неважные для решения поставленной задачи характеристики. Исходя из философского принципа «Бритва Оккама», следует строить теории так, чтобы они использовали достаточный минимум характеристик. Такое описание явления, содержащее только характеристики, необходимые для решения задачи, называется физической моделью явления.

Источник

Учебники

Журнал «Квант»

Общие

§17. Механические колебания

17.3 Простейшие колебательные системы.

17.3.1 Пружинный маятник.

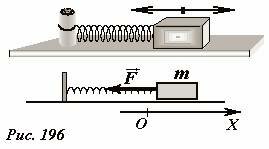
Рассмотрим движение небольшого бруска массой m, расположенного на гладкой горизонтальной поверхности и прикрепленного к неподвижному упору с помощью легкой пружины жесткости k (Рис. 196). Положение бруска будем описывать с помощью декартовой координаты x, начало отсчета которой совместим с положением, в котором пружина не деформирована. При отклонении бруска от положения равновесия на него будет действовать сила упругости пружины \(

\vec F\), направленная к положению равновесия, ее модуль определяется законом Гука \(F = kx\). На основании второго закона Ньютона и, пренебрегая трением, запишем уравнение, описывающее движение бруска

Из этого уравнения следует, что ускорение бруска зависит от его координаты

то есть пропорционально координате с отрицательным коэффициентом пропорциональности. Сравнивая с полученным ранее кинематическим уравнением, связывающим ускорение тела с его координатой

мы убеждаемся в их полной тождественности. На основании этого мы делаем обоснованный вывод: в рассматриваемой системе брусок совершает гармонические колебания \(x = A \cos (\omega t + \varphi_0)\). Частота этих колебаний не зависит от их амплитуды и легко находится из сравнения уравнений (2) и (3), идентичность которых требует выполнения условия \(

Период колебаний бруска равен

Полученные формулы для частоты и периода колебаний качественно легко объяснимы: частота колебаний возрастает с ростом жесткости пружины и убывает при возрастании массы груза.

Колебания, возникающие под действием внутренних возвращающих консервативных сил, называются свободными.

Подчеркнем, сейчас мы получили уравнение (2) на основании законов динамики, его совпадение с рассмотренным ранее кинематическим уравнением (3) заранее не предполагалось, это можно даже назвать «счастливым совпадением».

Закон движения бруска однозначно определяется при задании начальных условий. Зависимость параметров закона движения от начальных условий была рассмотрена нами ранее, поэтому здесь укажем только два крайних случая начальных условий.

Если мы отклоним брусок от положения равновесия на расстояние A и отпустим его без толчка (начальные условия: при t = 0 x₀ = A, υ₀ = 0), то закон движения будет иметь вид

В другом предельном случае, когда бруску резким толчком сообщают начальную скорость (начальные условия: при t = 0 x₀ = 0, υ = υ₀), закон движения будет несколько иным

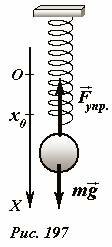
Рассмотрим теперь описание движения небольшого шарика массой m, подвешенного на легкой пружине жесткостью k (Рис. 197). Направим ось Ox вертикально вниз, начало отсчета совместим с положением недеформированной пружины. В процессе движения на шарик действуют сила тяжести \(

m \vec g\) и сила упругости \(

\vec F_\), модуль которой определяется законом Гука \(F_ = kx\). Уравнение второго закона Ньютона в проекции на введенную ось имеет вид

Так как сила упругости зависит от координаты шарика (следовательно, не постоянна), то движение шарика не будет равноускоренным. Понятно, что движение шарика будет колебательным, но, на первый взгляд, уравнение его движения (7) отличается от рассмотренного нами уравнения гармонических колебаний – присутствует постоянная составляющая mg. Преобразуем уравнение (7)

Появившаяся в уравнении величина \(

\omega = \sqrt<\frac>\). Таким образом, постоянная сила, действующая в колебательной системе, не изменяет частоты колебания, а только смещает положение равновесия. Полное решение уравнения движения (9) нам известно, поэтому можно также записать и полное решение уравнения (7) в исходной системе отсчета

в котором произвольные постоянные A, B определяются из начальных условий.

Еще одним общим методом получения уравнения движения является использование закона сохранения энергии. Рассмотрим превращения энергии в ходе колебаний бруска на гладкой горизонтальной поверхности (Рис. 196). Для того чтобы вывести брусок из положения равновесия к нему необходимо приложить внешнюю силу. Эта сила должна совершить положительную работу, тем самым, сообщая системе энергию. Эта энергия «запасается» в виде потенциальной энергии деформированной пружины и равна \(

U_0 = \frac<2>\). Если брусок еще и дополнительно толкнуть, то система получит дополнительную энергию в форме кинетической энергии бруска \(

Пренебрегая трением, закон сохранения механической энергии выражается уравнением

в котором сумма кинетической энергии бруска и потенциальной энергии деформированной пружины остается постоянной величиной, которая легко выражается через начальные условия \(

Зависимость скорости от времени описывается в этом случае функцией

Не сложно убедится, что эти функции при подстановке в уравнение (11) превращают его в верное тождество (конечно, при \(

\omega = \sqrt<\frac>\)), следовательно, функция (12) является решением этого уравнения.

Таким образом, уравнение (12) также является уравнением гармонических колебаний, оно полностью эквивалентно (равносильно) уравнению (1).

Для доказательства этого утверждения достаточно взять производную по времени от уравнения (11):

при выводе учтено, что производная от постоянной энергии равна нулю; учитывая, что производная от координаты равна скорости x′ = υ, а производная от координаты есть ускорение υ′ = a, получаем после сокращения уравнение (1) \(ma + kx = 0\). Можно также провести и обратный математический переход от уравнения (1) к уравнению (11).

после очевидного преобразования

Чтобы это уравнение превратилось в тождество необходимо, чтобы выполнялось условие \(

Подведем основной итог: если на основании физических законов (главным образом закона сохранения энергии) удалось показать, что некоторая переменная величина X(t) и ее производная V(t) = X′(t) связаны соотношением

то величина X изменяется по гармоническому закону, с круговой частотой ω.

17.3.2 Математический маятник.

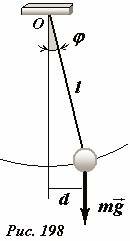
Небольшой шарик, подвешенный на легкой нерастяжимой нити, способен совершать свободное колебательное движение (Рис. 198). Для описания движения маятника будем считать шарик материальной точкой, пренебрежем массой нити и сопротивлением воздуха. Такая модель называется математическим маятником.

В качестве координаты, описывающей положение шарика, выберем угол отклонения нити от вертикали φ. Для описания изменения этой координаты удобно использовать уравнение динамики вращательного движения

Это уравнение описывает колебания маятника, но не является уравнением гармонических колебаний, так как момент сил пропорционален синусу угла отклонения, а не самому углу. Однако, если считать углы отклонения малыми (сколько это – мы выясним позднее), можно воспользоваться приближенной формулой \(\sin \varphi \approx \varphi\) в этом приближении уравнение (3) превращается в знакомое уравнение гармонических колебаний

Период малых колебаний маятника выражается через круговую частоту

Так как малые колебания математического маятника являются гармоническими, то их период не зависят от амплитуды. Этот факт был экспериментально отмечен еще Г. Галилеем. При больших углах отклонения период колебаний математического маятника незначительно возрастает.

Отметим, что период колебаний математического маятника не зависит также от массы шарика – вспомните, ускорение свободного падения, а также другие характеристики движения тела в поле тяжести Земли также не зависят от массы тела (если, конечно, пренебрегать сопротивлением воздуха). Формула (6) может быть использована и используется для экспериментального определения ускорения свободного падения. Длина нити и период колебаний достаточно просто измерить экспериментально, затем с помощью формулы (6) можно рассчитать ускорение свободного падения.

Попробуем описать движение математического маятника с помощью закона сохранения механической энергии. Кинетическая энергия шарика выражается формулой \(

E_ = \frac <2>= \frac<2>\). Нулевой уровень отсчета потенциальной энергии совместим с точкой подвеса нити, тогда потенциальная энергия шарика равна \(U = −mgl \cos \varphi\). Уравнения закона сохранения механической энергии (с учетом начальных условий) имеет вид

Это уравнение также не является уравнением гармонических колебаний. Но, если мы опять будем считать углы отклонения маятника малыми и воспользуемся приближенной формулой \(

Конечно, такое совпадение не является случайным – фактически в обоих подходах мы использовали одно и то же приближение малых углов отклонения.

17.3.3 Математический маятник с пружиной.

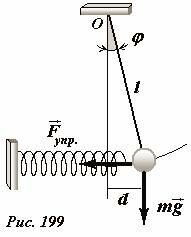
Рассмотрим еще один пример колебательной системы, являющейся «гибридом» математического и пружинного маятника (Рис. 199): к шарику, подвешенному на нити длиной l, прикреплена легкая пружина так, что в положении равновесия нить маятника располагается вертикально (в этом случае пружина не деформирована). По-прежнему, положение маятника будем описывать с помощью угла отклонения φ, который будем считать малым. Уравнение динамики вращательного движения относительно точки подвеса для шарика будет иметь вид

Это уравнение является уравнением гармонических колебаний: ускорение пропорционально смещения от положения равновесия. Круговая частота этих колебаний равна

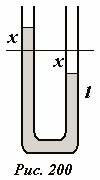
17.3.4 Колебание жидкости в трубке.

\upsilon = \frac<\Delta x><\Delta t>\). Следовательно, кинетическая энергия движущейся жидкости равна

где первое слагаемое равно потенциальной энергии жидкости в левом колене трубки, второе – в правом. Если пренебречь неизбежными потерями механической энергии из-за сил вязкого трения, то сумма кинетической и потенциальной энергии жидкости постоянна, поэтому

Из этого уравнения следует, что движение жидкости подчиняется уравнению гармонических колебаний

с круговой частотой \(

Отметим, что описать движение жидкости на основании уравнений динамики в данном случае сложнее.

Источник

§ 87. Близкодействие и действие на расстоянии

Как передаётся действие Земли на парящие в воздухе тела?

Как вызвать движение велосипеда?

Закон взаимодействия неподвижных электрических зарядов был установлен экспериментально. Но оставался нерешённым вопрос о том, как осуществляется это взаимодействие.

Близкодействие. Если мы наблюдаем действие одного тела на другое, находящееся на некотором расстоянии от него, то, прежде чем допустить, что это действие прямое и непосредственное, мы склонны сначала исследовать, нет ли между телами какой-либо материальной связи: нитей, стержней и т. д. Если подобные связи есть, то мы объясняем действие одного тела на другое при помощи этих промежуточных звеньев.

При игре в теннис посредниками, передающими взаимодействие теннисистов, являются ракетки и мяч.

При подъёме груза используется подъёмный кран, которым управляет крановщик, находящийся в кабине.

Водитель автобуса заставляет дверь открываться, направляя по трубкам сжатый воздух в цилиндр, управляющий механизмом двери.

Приведите примеры передачи механического воздействия без непосредственного контакта тел.

Во всех трёх примерах мы видим ряд последовательных действий, в результате которых совершается некоторый физический процесс. С помощью этого процесса, распространяющегося от точки к точке, происходит передача действия, причём не мгновенно, а с той или иной скоростью.

Итак, действие между телами на расстоянии во многих случаях можно объяснить присутствием передающих действие промежуточных звеньев. Не разумно ли в тех случаях, когда мы не замечаем никакой среды, никакого посредника между взаимодействующими телами, допустить существование некоторых промежуточных звеньев? Ведь иначе придётся считать, что тело действует там, где его нет.

Кому незнакомы свойства воздуха, тот может подумать, что рот или голосовые связки собеседника непосредственно действуют на уши, и считать, что звук передаётся невидимой средой, свойства которой непонятны. Однако можно проследить весь процесс распространения звуковых волн и вычислить их скорость.

Важно
Согласно теории близкодействия взаимодействие между удалёнными друг от друга телами всегда осуществляется с помощью промежуточных звеньев (или среды), передающих взаимодействие от точки к точке.

Многие учёные, сторонники теории близкодействия, для объяснения происхождения гравитационных и электромагнитных сил придумывали невидимые истечения, окружающие планеты и магниты, незримые атмосферы вокруг наэлектризованных тел. Размышления эти были подчас весьма остроумны, но обладали немаловажным недостатком — они ничего не давали науке.

Действие на расстоянии (дальнодействие). Так продолжалось до тех пор, пока Ньютон не установил закон всемирного тяготения. Последовавшие успехи в исследовании Солнечной системы настолько захватили воображение учёных, что они вообще в большинстве своём начали склоняться к мысли о бесполезности поисков каких-либо посредников, передающих взаимодействие от одного тела к другому.

Возникла теория прямого действия на расстоянии через пустоту.

Важно
Согласно теории дальнодействия действие передаётся мгновенно на сколь угодно большие расстояния. Тела способны «чувствовать» присутствие друг друга без какой-либо среды между ними.

Сторонников действия на расстоянии не смущала мысль о действии тела там, где его самого нет. «Разве, — рассуждали они, — мы не видим, как магнит или наэлектризованная палочка прямо через пустоту притягивают тела?» И при этом сила притяжения, например, магнита заметно не меняется, если магнит завернуть в бумагу или положить в деревянный ящик. Более того, даже если нам и кажется, что взаимодействие тел вызвано непосредственным контактом, то в действительности это не так. При самом тесном контакте между телами или частями одного тела остаются небольшие промежутки. Ведь груз, например подвешенный на нити, не разрывает эту нить, хотя между отдельными атомами, из которых она состоит, ничего нет. Действие на расстоянии — единственный способ действия, встречающийся повсюду.

Возражения против теории близкодействия были довольно сильными, тем более что они подкреплялись успехами, которых добились такие убеждённые сторонники действия на расстоянии, как Кулон и Ампер.

Если бы развитие науки происходило прямолинейно, то, казалось бы, победа теории действия на расстоянии обеспечена. Но в действительности развитие науки напоминает, скорее, спиралеобразную линию. Пройдя один виток, наука возвращается примерно к тем же представлениям, но уже на более высоком уровне. Именно так произошло при развитии молекулярно-кинетической теории. Атомная гипотеза Демокрита одно время была оставлена большинством учёных. Затем она возродилась в строгой математической форме и была доказана экспериментально. Так же случилось и при развитии теории близкодействия.

Успехи в открытии законов взаимодействия электрических зарядов и токов не были неразрывно связаны с представлением о действии на расстоянии. Ведь опытное исследование самих сил не предполагает наличия определённых представлений о том, как эти силы передаются. В первую очередь нужно было найти математическое выражение для сил, а выяснить их природу можно было и потом.

Ключевые слова для поиска информации по теме параграфа.
Близкодействие. Дальнодействие

1. Какая теория — дальнодействия или близкодействия — кажется вам более привлекательной? Почему?

2. Каковы сильные стороны теории дальнодействия по сравнению с теорией близкодействия?

Источник