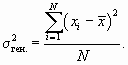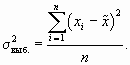Для чего используют выборочное наблюдение
Выборочное наблюдение в статистике
11.1. Основные положения теории выборочного метода наблюдения
Суть выборочного метода заключается в отборе отдельных единиц обследуемой совокупности по специальным правилам, гарантирующим реализацию принципа случайности отбора, с целью получения обобщающих статистических характеристик изучаемой совокупности.
Выборочный метод позволяет получать достоверные результаты лишь тогда, когда соблюдается принцип равновозможности каждой единицы быть отобранной. При этом только случай, а не какой-либо иной фактор, влияет на решение включить рассматриваемую единицу в выборочную совокупность или нет. Из всех методов несплошного наблюдения выборочный считается наиболее теоретически разработанным. Положенный в его основу принцип случайности позволяет математически обосновать дальнейшее распространение выборочных характеристик на всю совокупность.
Выборочная совокупность репрезентативна (представительна) в том случае, если она верно отражает закономерности, структуру генеральной совокупности.
Широкое применение выборочного метода в статистической практике объясняется рядом его преимуществ по сравнению со сплошным наблюдением. Основными являются:
Вместе с тем выборочный метод имеет ряд недостатков. Важнейший из них связан с наличием ошибок репрезентативности, которые обусловлены тем, что наблюдаются не все единицы изучаемой совокупности. Кроме того, его проведение требует привлечения высококвалифицированного персонала, что в свою очередь ведет к увеличению стоимости обследования.
11.1.1. Основные определения и обозначения
В теории выборочного наблюдения используются специфические понятия, определения и обозначения.
Под термином генеральная совокупность понимается изучаемая статистическая совокупность, из которой проводится отбор единиц для непосредственного наблюдения (количество единиц генеральной совокупности обозначается через N).
Доля выборочной совокупности в общем объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки, процентом отбора):
Среднее значение признака в выборочной совокупности обозначается через x. Оно исчисляется как
Дисперсия единиц количественного признака определяется следующим образом:
Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно принимают ее равной дисперсии, рассчитываемой по выборочным данным;
Наряду с нахождением характеристик количественных признаков могут оцениваться характеристики альтернативных показателей.
Дисперсия альтернативного признака рассчитывается следующим образом:
Основной целью статистического наблюдения является получение достоверной статистической информации. Но при любом способе наблюдения могут возникнуть погрешности, которые приведут к снижению качества получаемой информации. Эти погрешности называются ошибками наблюдения. При сплошном наблюдении возможны только ошибки регистрации (случайные и систематические). При выборочном наблюдении возможны как ошибки регистрации, так и ошибки репрезентативности. Те и другие могут носить как случайный, так и систематический характер.
Задача выборочного наблюдения состоит в измерении случайной ошибки репрезентативности, которая возникает вследствие несплошного характера наблюдения при любом способе отбора.
11.1.2. Основные этапы работ при организации выборочного наблюдения
К основным этапам работ при организации выборочного наблюдения относятся:
11.1.3. Роль закона больших чисел при определении ошибок выборочного наблюдения
Центральное место в теории выборочного наблюдения занимает задача оценки репрезентативности выборочной совокупности. Ошибки репрезентативности представляют собой отклонения характеристик выборочной совокупности от характеристик генеральной.
Теория оценивания ошибок выборки базируется на ряде предельных теорем под общим названием «закон больших чисел». В них доказывается, что ошибки могут быть сведены к минимальным значениям. При этом возможно установить их значения с требуемой точностью.
Так, в приложении к выборочному методу из теоремы Чебышева следует, что с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки, полученной с соблюдением всех правил ее формирования, разность между генеральной и выборочной средними будет сколь угодно мала. Теорема Ляпунова позволяет оценить предельную ошибку выборки для среднего значения признака. Теорема Бернулли является частным случаем теоремы Чебышева применительно к исследованию доли альтернативного признака.
11.1.4. Способы отбора единиц в выборочную совокупность. Классификация видов выборочного наблюдения
Различают индивидуальный, групповой и комбинированный отбор.
При групповом отборе единицы отбираются группами; ими могут быть, например, бригады, микрорайоны (этот вид отбора свойственен для серийной выборки).
Кроме того, каждый из перечисленных способов отбора может быть бесповторным или повторным.
Бесповторным является такой отбор, в результате которого однажды отобранная в выборку единица наблюдения не может быть отобранной из генеральной совокупности во второй раз. При повторном отборе попавшая в выборку единица наблюдения вновь возвращается в совокупность, и ее можно отобрать во второй, третий раз и т.д.
В статистике встречаются разнообразные виды выборок: собственно-случайная выборка, механическая, типическая, серийная, комбинированная. Свои особенности имеет малая выборка.
Вид выборки определяется задачами исследования, полнотой и особенностями информации, которой мы располагаем об объекте наблюдения.
Собственно-случайная выборка. Отбор единиц при использовании собственно случайной выборки производится путем жеребьевки или с использованием таблицы случайных чисел. При этом все единицы совокупности должны иметь равные шансы попасть в выборочную совокупность.
Таблица случайных чисел представляет собой набор колонок случайных цифр. Случайность сочетания определяется отсутствием закона их расположения и приблизительно равной частотой встречаемости каждой из десяти цифр при образовании случайного числа.
Существует множество методов составления таблиц случайных чисел. В наше время они генерируются с помощью датчика случайных чисел. Его содержат все современные статистические пакеты прикладных программ, а также Excel, входящий в набор стандартных программ для Windows.
Пример 11.1. Предположим нужно отобрать 15 студентов из 200, обучающихся на первом курсе, методом случайной бесповторной выборки.
| Ряд | 01 | 02 | 03 | 04 | 05 | 06 | |
|---|---|---|---|---|---|---|---|
| Колонка | 1 | 66194 | 78240 | 00833 | 12111 | 47189 | 76396 |
| 2 | 28926 | 43195 | 88000 | 86683 | 99951 | 72486 | |
| Ряд | 07 | 08 | 09 | 10 | 11 | 12 | |
| Колонка | 1 | 46409 | 74626 | 34450 | 36327 | 74185 | 12296 |
| 2 | 17469 | 22111 | 81974 | 72135 | 77536 | 41623 | |
| Ряд | 13 | 14 | 15 | 16 | 17 | 18 | |
| Колонка | 1 | 60822 | 72121 | 95268 | 92603 | 18813 | 38840 |
| 2 | 60280 | 79152 | 41377 | 09091 | 90291 | 26903 | |
| Ряд | 19 | 20 | 21 | 22 | 23 | 24 | |
| Колонка | 1 | 05959 | 85141 | 75047 | 30752 | 22986 | 99439 |
| 2 | 33836 | 21155 | 59643 | 95260 | 82575 | 86692 | |
| Ряд | 25 | 26 | 27 | 28 | 29 | 30 | |
| Колонка | 1 | 20389 | 39249 | 96777 | 04860 | 41613 | 17930 |
| 2 | 93029 | 05173 | 33605 | 32918 | 42375 | 00794 | |
| Ряд | 31 | 32 | 33 | ||||
| Колонка | 1 | 24649 | 79899 | 76801 | |||
| 2 | 31845 | 34061 | 49594 | ||||
Проведем отбор с помощью таблицы случайных чисел следующим образом:
В итоге получим следующие числа:
194, 111, 189, 185, 121, 141, 047,
195, 135, 152, 091, 155, 029, 173, 061.
В выборочную совокупность должны быть включены студенты, индивидуальные номера которых в исходном списке соответствуют отобранным числам. Таким образом, в выборку попали студенты, имеющие следующие номера в списке:
029, 047, 061, 091, 111, 121, 135,
141, 152, 155, 173, 185, 189, 194, 195.
Механическая выборка. Наряду со случайным отбором в практике выборочного наблюдения применяется механический отбор. При этом все единицы генеральной совокупности нумеруются числами от 1 до N, после чего отбирается каждая (N/n)-я единица для обследования. Величина N/n называется шагом, или интервалом, отбора.
Допустим, надо отобрать 50 студентов из 200, обучающихся на первом курсе, методом механической выборки. Для этого необходимо сделать следующее:
Типическая выборка. В случае использования типической выборки cовокупность предварительно разбивается на однородные типы или группы, а затем производится случайный (или механический) отбор единиц наблюдения внутри полученных групп. Извлеченная подобным образом выборка будет типической (в литературе она также называется расслоенной, стратифицированной, районированной).
Типическая выборка в статистической практике применяется гораздо чаще, чем остальные виды выборочного наблюдения. Так, при обследованиях населения в зависимости от целей исследования генеральную совокупность расслаивают по возрастному или социальному признаку, типу проживания (городское, сельское населения и т.д.); при обследованиях малых предприятий типизация осуществляется по четырем признакам: территориальному, отраслевому, виду собственности и размеру выручки. Этим достигается однородность единиц внутри групп. Типическая выборка дает более точные результаты.
Серийная (гнездовая) выборка. Если генеральную совокупность можно разделить на одинаковые по объему и однородные группы, то целесообразно осуществлять отбор не единиц, а их серий. После такого отбора внутри серий проводится сплошное обследование.
Например, при оценке качества продукции можно отбирать партии товара, а затем обследовать все входящие в них изделия; при некоторых обследованиях населения отбираются в порядке серий жилые дома, в которых опрашиваются жильцы всех квартир; обследования школьников проводятся путем отбора однотипных школ или конкретных классов, ученики которых подвергаются сплошному опросу, и т.д.
Комбинированные выборки. Комбинированный отбор широко применяется на практике и представляет собой сочетание разных методов отбора (их комбинацию), например типического с механическим. В этом случае генеральная совокупность разбивается на типические группы на основе ранее выбранного группировочного признака, внутри этих групп единицы наблюдения упорядочиваются, устанавливается шаг отбора, соответствующий необходимой численности выборки, после чего происходит извлечение единиц наблюдения из типических групп на основе механического отбора. Подобная комбинация методов обеспечивает представительство в выборке всех типов единиц наблюдения (за счет применения типического отбора) и сохраняет структуру типических групп по группировочным признакам, обеспечиваемую механическим отбором.
Малая выборка. Выборка считается малой, если количество объектов, отобранных для выборочного наблюдения, не превышает 20 единиц.
Малые выборки используются в тех ситуациях, когда распределение признака в генеральной совокупности является нормальным или приближается к нему. Только в этих случаях построенные доверительные интервалы или рассчитанные доверительные вероятности будут иметь реальное практическое значение.
Выборочное наблюдение в статистике
Понятие и виды выборочного наблюдения
Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Качество выборочных наблюдений зависит и от типа выборки: повторная или бесповторная.
При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Ошибки выборки
Выборочную совокупность можно сформировать по количественному признаку статистических величин, а также по альтернативному или атрибутивному. В первом случае обобщающей характеристикой выборки служит выборочная средняя величина, обозначаемая 

Разности 

Величина ошибки выборки может быть разной для разных выборок из одной генеральной совокупности, поэтому в статистике определяется средняя ошибка повторной и бесповторной выборки по формулам:


где Дв — выборочная дисперсия.
Например, на заводе с численностью работников 1000 чел. проведена 5%-ая случайная бесповторная выборка с целью определения среднего стажа работников. Результаты выборочного наблюдения приведены в первых двух столбцах следующей таблицы: