Диаметр умножить на высоту что получится
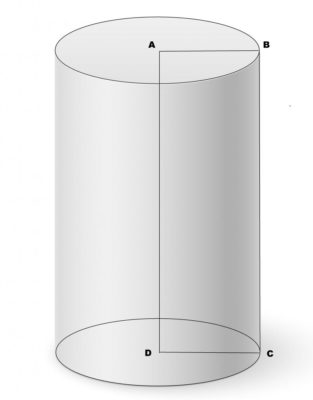
Диаметр и высота цилиндра
Свойства
Через диаметр цилиндра можно рассчитать его радиус и периметр основания цилиндра. Радиус будет равен половине диаметра, а периметр – его произведению на число π. r=D/2 P=πD
Зная диаметр и высоту цилиндра, можно узнать площадь, объем, диагональ цилиндра и остальные параметры. Площадь боковой поверхности цилиндра представляет собой площадь прямоугольника, сторонами которого являются периметр основания цилиндра и его высота. Чтобы затем найти площадь полной поверхности цилиндра через диаметр и высоту, нужно к площади боковой поверхности добавить площадь верхнего и нижнего оснований, каждое из которых равно произведению числа π на четверть квадрата диаметра. S_(б.п.)=hP=πDh S_(п.п.)=S_(б.п.)+2S_(осн.)=πDh+(πD^2)/2=πD/2(2h+D) P=πD
Объем цилиндра представляет собой площадь его основания, умноженную на высоту. Чтобы найти объем цилиндра через диаметр и высоту, нужно умножить квадрат диаметра на четверть числа π и на высоту. V=(πD^2 h)/4 P=πD
Диагональ цилиндра находится из прямоугольного треугольника, в котором она является гипотенузой, а катеты представлены высотой и диаметром цилиндра. По теореме Пифагора диагональ цилиндра через высоту и диаметр цилиндра равна квадратному корню из суммы их квадратов. (рис. 25.1) d=√(h^2+D^2 ) P=πD
Чтобы найти радиус сферы вписанной в цилиндр, если его диаметр равен высоте, нужно разделить диаметр цилиндра либо высоту на два, так как радиус вписанной сферы равен радиусу цилиндра. (рис.25.2) r_1=h/2=D/2 P=πD
Радиус сферы, описанной вокруг цилиндра, при соблюдении тех же условий (равенство диаметра цилиндра и его высоты) равен половине диагонали цилиндра.(рис.25.3) R=d/2=√(h^2+D^2 )/2
Как найти объем цилиндра: формула через диаметр и высоту
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
Объем цилиндра формула (через радиус основания и высоту)
r — радиус основания цилиндра,
h — высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ ( 1 /2) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
2. Через радиус основания и высоту
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2) 2 ⋅ H
Введите радиус основания и высоту цилиндра
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула объема цилиндра:

Примеры задач
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Поэтапный расчет объема картонной коробки
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b; Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |

Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м 3 ;
зная равенство: 1 м 3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Цилиндр может быть правильным или наклонным
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник 
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Как найти высоту цилиндра, с помощью данных?
Объем цилиндра формула (через радиус основания и высоту)
r — радиус основания цилиндра,
h — высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что
S (б.п.) = hP = 2πrh
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
2. Через радиус основания и высоту
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2) 2 ⋅ H
Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.
Расшифровать формулу просто:
То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.
Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.
Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.
Способ расчета радиуса цилиндра:
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
R = √V / πh
где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
Примеры задач
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Решение:
Применим формулу, в которой задействованы заданные величины:
Решение:
Используем третью формулу для нахождения неизвестной величины:
Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
S = 2 π Rh
Площадь полной поверхности цилиндра через радиус основания и высоту
Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:
, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.
Как найти объём геометрических фигур
Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м 3 ).
Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.
Содержание:
Как найти объем трехмерных объектов
Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.
Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м 3 /1000000 = 0,004256 м 3
Как найти объем для фигур цилиндрической формы
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.
Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.
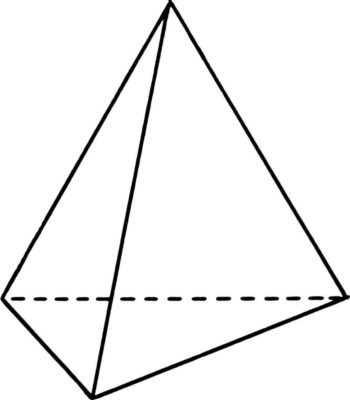
Как рассчитать объем треугольной пирамиды
Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.
Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.
В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.
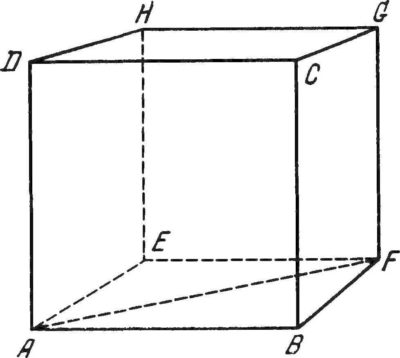
Как посчитать объем куба
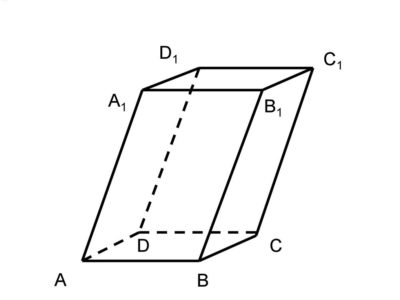
Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.
Как найти объем прямоугольного параллелепипеда
Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:
Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см 3
Советы по измерению:
Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.
Как найти объем цилиндра
Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:
Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:
3,14 * 2 см 2 * 5 см = 62.831853071796 = 63см 3
Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.
Как найти объем пирамиды
фото 6 — посчитать объём
Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:
Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:
V = 3 * 2 = 2 см 3 ‒ это и будет являться объемом искомой геометрической фигуры.
Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.
Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.
Как посчитать объём в емкостях различных форм?
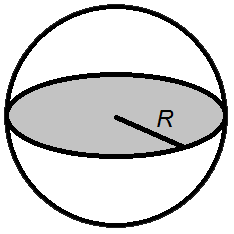
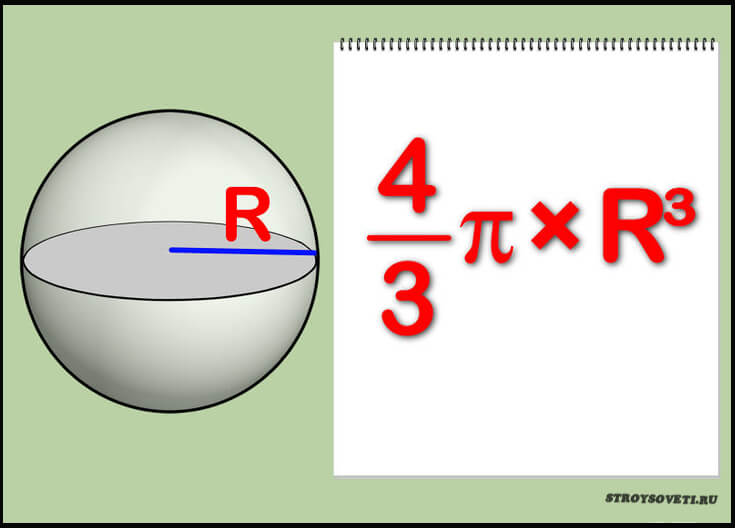
1 Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592
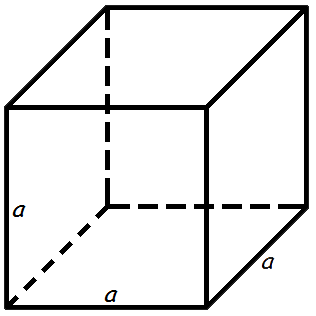
2 Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3где V — объем куба,
a — длина грани куба
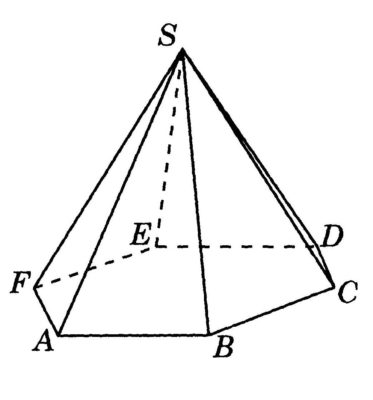
3 Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды
4 Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · hгде V – объем параллелепипеда,
So – площадь основания,
h – длина высоты
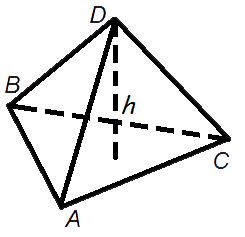
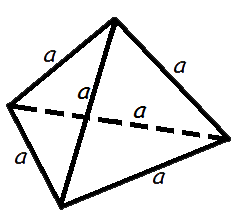
5 Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V – объем правильного тетраэдра,
a – длина ребра правильного тетраэдра
6 Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
| V = | 1 | π R2h |
| 3 |
| V = | 1 | So h |
| 3 |
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.141592.
7 Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So hгде V – объем призмы,
So – площадь основания призмы,
h – высота призмы
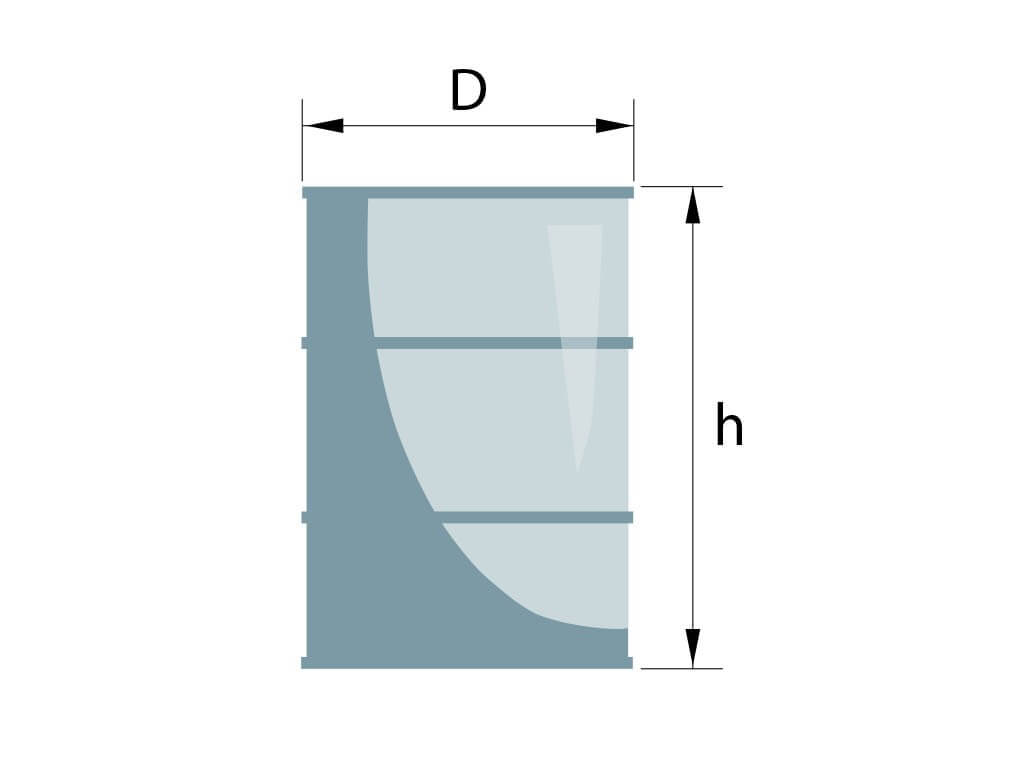
8 Как высчитать объем бочки в литрах?
Теперь, когда мы знаем объем бочки в м.куб, можно перевести это значение в литры, а для этого использую соотношение: 1 куб. метр = 1000 литров.
Тогда, объем бочки в литрах будет равен:
0.31 м3 * 1000 литров = 310 литров
9 Как найти объем бочки по диаметру?
Для того, чтобы найти объем бочки по диаметру необходимо преобразовать стандартную формулу, по которой обычно находят объем цилиндра через радиус и высоту:
Зная, что диаметр равен двум радиусам, получаем следующую формулу, которую можно применить для нахождения объема бочки в м3, по диаметру и высоте:
Все расчеты необходимо проводить в единой мере измерения длины, в нашем случае — это метры.
Для примера, необходимо найти объем цилиндрической бочки зная диаметр и высоту:
Подставляем данные в формулу, предварительно переведя см в метры:
V бочки в м3 = 3,14159 * (0,84 м)² / 4 * 0,56 м = 0,3103 м3
Если округлить, то получается, что объем цилиндрической бочки с размерами D = 84 см, h = 56 см = 0,31 м3
10 Как узнать объём прямоугольной тары
Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему
V=a*b*c, где a, b и с – стороны тары.
Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.
11 Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
12 Как вычислить объём цистерны выполненной в виде цилиндра
Подобные геометрические фигуры используются для хранения пищевых продуктов, транспортирования топлива и других целей. Многие не знают, как рассчитать объем воды, но основные нюансы такого процесса опишем дальше в нашей статье.
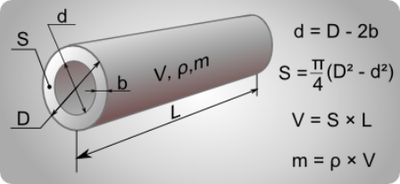
Высоту жидкости в цилиндрической ёмкости определяют по специальному устройству метрштоку. В данном случае емкость цистерны вычисляется по специальным таблицам. Изделия со специальными таблицами измерения объёма в жизни встречаются редко, поэтому подойдём к решению проблемы другим путём и опишем, как рассчитать объём цилиндра по специальной формуле – V=S*L, где
Показатель L можно измерить при помощи всё той же рулетки, но площадь сечения цилиндра придётся считать. Показатель S вычисляют по формуле S=3,14*d*d/4, где d – диаметр окружности цилиндра.
А теперь ознакомимся с конкретным примером. Допустим, длина нашей цистерны имеет значение 5 метров, её диаметр 2,8 метра. Сначала вычислим площадь сечения геометрической фигуры S= 3,14*2,8*2,8/4=6,15м. А теперь можно приступать к вычислению объёма цистерны 6,15*5= 30,75 м³.
12.1 Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
13 Внутренний объем погонного метра трубы в литрах — таблица
Таблица показывает внутренний объем погонного метра трубы в литрах. То есть сколько потребуется воды, антифриза или другой жидкости (теплоносителя), чтобы заполнить трубопровод. Взят внутренний диаметр труб от 4 до 1000 мм.
| 4 | 0.0126 | 0.1257 |
| 5 | 0.0196 | 0.1963 |
| 6 | 0.0283 | 0.2827 |
| 7 | 0.0385 | 0.3848 |
| 8 | 0.0503 | 0.5027 |
| 9 | 0.0636 | 0.6362 |
| 10 | 0.0785 | 0.7854 |
| 11 | 0.095 | 0.9503 |
| 12 | 0.1131 | 1.131 |
| 13 | 0.1327 | 1.3273 |
| 14 | 0.1539 | 1.5394 |
| 15 | 0.1767 | 1.7671 |
| 16 | 0.2011 | 2.0106 |
| 17 | 0.227 | 2.2698 |
| 18 | 0.2545 | 2.5447 |
| 19 | 0.2835 | 2.8353 |
| 20 | 0.3142 | 3.1416 |
| 21 | 0.3464 | 3.4636 |
| 22 | 0.3801 | 3.8013 |
| 23 | 0.4155 | 4.1548 |
| 24 | 0.4524 | 4.5239 |
| 26 | 0.5309 | 5.3093 |
| 28 | 0.6158 | 6.1575 |
| 30 | 0.7069 | 7.0686 |
| 32 | 0.8042 | 8.0425 |
| 34 | 0.9079 | 9.0792 |
| 36 | 1.0179 | 10.1788 |
| 38 | 1.1341 | 11.3411 |
| 40 | 1.2566 | 12.5664 |
| 42 | 1.3854 | 13.8544 |
| 44 | 1.5205 | 15.2053 |
| 46 | 1.6619 | 16.619 |
| 48 | 1.8096 | 18.0956 |
| 50 | 1.9635 | 19.635 |
| 52 | 2.1237 | 21.2372 |
| 54 | 2.2902 | 22.9022 |
| 56 | 2.463 | 24.6301 |
| 58 | 2.6421 | 26.4208 |
| 60 | 2.8274 | 28.2743 |
| 62 | 3.0191 | 30.1907 |
| 64 | 3.217 | 32.1699 |
| 66 | 3.4212 | 34.2119 |
| 68 | 3.6317 | 36.3168 |
| 70 | 3.8485 | 38.4845 |
| 72 | 4.0715 | 40.715 |
| 74 | 4.3008 | 43.0084 |
| 76 | 4.5365 | 45.3646 |
| 78 | 4.7784 | 47.7836 |
| 80 | 5.0265 | 50.2655 |
| 82 | 5.281 | 52.8102 |
| 84 | 5.5418 | 55.4177 |
| 86 | 5.8088 | 58.088 |
| 88 | 6.0821 | 60.8212 |
| 90 | 6.3617 | 63.6173 |
| 92 | 6.6476 | 66.4761 |
| 94 | 6.9398 | 69.3978 |
| 96 | 7.2382 | 72.3823 |
| 98 | 7.543 | 75.4296 |
| 100 | 7.854 | 78.5398 |
| 105 | 8.659 | 86.5901 |
| 110 | 9.5033 | 95.0332 |
| 115 | 10.3869 | 103.8689 |
| 120 | 11.3097 | 113.0973 |
| 125 | 12.2718 | 122.7185 |
| 130 | 13.2732 | 132.7323 |
| 135 | 14.3139 | 143.1388 |
| 140 | 15.3938 | 153.938 |
| 145 | 16.513 | 165.13 |
| 150 | 17.6715 | 176.7146 |
| 160 | 20.1062 | 201.0619 |
| 170 | 22.698 | 226.9801 |
| 180 | 25.4469 | 254.469 |
| 190 | 28.3529 | 283.5287 |
| 200 | 31.4159 | 314.1593 |
| 210 | 34.6361 | 346.3606 |
| 220 | 38.0133 | 380.1327 |
| 230 | 41.5476 | 415.4756 |
| 240 | 45.2389 | 452.3893 |
| 250 | 49.0874 | 490.8739 |
| 260 | 53.0929 | 530.9292 |
| 270 | 57.2555 | 572.5553 |
| 280 | 61.5752 | 615.7522 |
| 290 | 66.052 | 660.5199 |
| 300 | 70.6858 | 706.8583 |
| 320 | 80.4248 | 804.2477 |
| 340 | 90.792 | 907.9203 |
| 360 | 101.7876 | 1017.876 |
| 380 | 113.4115 | 1134.1149 |
| 400 | 125.6637 | 1256.6371 |
| 420 | 138.5442 | 1385.4424 |
| 440 | 152.0531 | 1520.5308 |
| 460 | 166.1903 | 1661.9025 |
| 480 | 180.9557 | 1809.5574 |
| 500 | 196.3495 | 1963.4954 |
| 520 | 212.3717 | 2123.7166 |
| 540 | 229.0221 | 2290.221 |
| 560 | 246.3009 | 2463.0086 |
| 580 | 264.2079 | 2642.0794 |
| 600 | 282.7433 | 2827.4334 |
| 620 | 301.9071 | 3019.0705 |
| 640 | 321.6991 | 3216.9909 |
| 660 | 342.1194 | 3421.1944 |
| 680 | 363.1681 | 3631.6811 |
| 700 | 384.8451 | 3848.451 |
| 720 | 407.1504 | 4071.5041 |
| 740 | 430.084 | 4300.8403 |
| 760 | 453.646 | 4536.4598 |
| 780 | 477.8362 | 4778.3624 |
| 800 | 502.6548 | 5026.5482 |
| 820 | 528.1017 | 5281.0173 |
| 840 | 554.1769 | 5541.7694 |
| 860 | 580.8805 | 5808.8048 |
| 880 | 608.2123 | 6082.1234 |
| 900 | 636.1725 | 6361.7251 |
| 920 | 664.761 | 6647.6101 |
| 940 | 693.9778 | 6939.7782 |
| 960 | 723.8229 | 7238.2295 |
| 980 | 754.2964 | 7542.964 |
| 1000 | 785.3982 | 7853.9816 |
Если у вас специфическая конструкция или труба, то в формуле выше показано как вычислить точные данные для правильного расхода воды или иного теплоносителя.
13.1 Расчет объема воды, находящейся во всей системе
Для определения такого параметра, необходимо в формулу подставить значение внутреннего радиуса. Однако сразу появляется проблема. А как рассчитать полный объем воды в трубе всей отопительной системы, в которую входят:
Когда установлен биметаллический радиатор, это значение намного меньше. Количество воды в котле можно узнать из паспорта устройства.
Для определения объема расширительного бака, его заполняют измеренным заранее, количеством жидкости.
Очень просто определяется объём труб. Имеющиеся данные для одного метра, определенного диаметра, нужно просто умножить на длину всего трубопровода.
Заметим что в глобальной сети и справочной литературе, можно увидеть специальные таблицы. Они показывают ориентировочные данные изделия. Погрешность приведенных данных достаточно мала, поэтому приведенные в таблице значения, можно смело использовать для вычисления объема воды.
Надо сказать, что при расчете значений, нужно учитывать некоторые характерные отличия. Металлические трубы, имеющие большой диаметр, пропускают количество воды, значительно меньше, чем такие же полипропиленовые трубы.
Причина кроется в гладкости поверхности труб. У стальных изделий она выполнена с большой шероховатостью. ППР трубы не имеют шероховатости на внутренних стенках. Однако при этом стальные изделия имеют больший объем воды, чем в других трубах, одинакового сечения. Поэтому чтобы убедиться, что расчет объема воды в трубах произведен верно, нужно несколько раз перепроверить все данные и подкрепить результат онлайн-калькулятором.
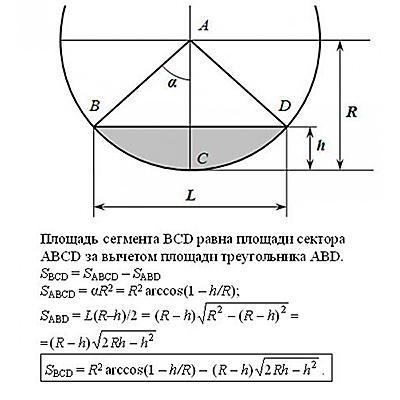
Формула определения площади сечения неполностью заполненных труб:
14 Способы перевода кубометров в другие кубические единицы
Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.
Если V измерен в мм3, см3, дм3, л, то в м3 переводим соответственно:
Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м3), получим V материала (м3).
Подсчитать кубические метры не составляет трудностей для человека, не имеющего математических наклонностей, несмотря на то что в каждом случае требуется разный подход.
Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.