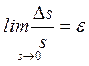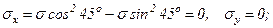Деформация и перемещение в чем разница
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.
Рабочие гипотезы СОПРОМАТА
ОТВЕТ: В отличие от термеха, базирующегося на модели абс. твердого тела, в сопромате принята своя расчетная модель-модель идеализированного деформируемого тела. А для упрощения расчетов принимаются следующие допущения или гипотезы: 1) Материал тела имеет сплошное строение. 2) материал однороден, т.е. во всех точках свойства одинаковы. 3) материал изотропен, т.е. по всем направлениям свойства одинаковы. 4) до приложения внешних сил начальные напряжения в материале отсутствуют. 5) при решении реальных задач целесообразно использовать принцип суперпозиции, или принцип независимости действия сил, т.е. воздействие на конструкцию группы сил равно сумме воздействий от каждой силы в отдельности и не зависит от последовательности приложения этих сил.
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ И МЕТОД ИХ ОПРЕДЕЛЕНИЯ.
ОТВЕТ: Под действием внешних сил на брус возникают внутренние силы или внутренние силовые факторы, для определения которых в сопромате принят единый расчетный метод – метод сечений. 1) разрезаем мысленно брус в исследуемом сечении на 2 части I и II. 2) Отбрасываем одну из частей. 3) Заменяем действие отбрасываемой части II на часть I внутренними силовыми факторами(в общем случае их 6). Qx Qy – поперечные силы, Nz – продольная сила, Mx My – изгибающие моменты, Mz – крутящий момент. 4) Уравновешиваем оставшуюся часть бруса и с помощью уравнений равновесия термеха находим искомые силовые факторы.
ПОНЯТИЕ О НАПРЯЖЕНИЯХ, ДЕФОРМАЦИЯХ И ПЕРЕМЕЩЕНИЯХ.
ОТВЕТ: Мерой интенсивности действия внутренних сил в окрестности точки рассматриваемого поперечного сечения являются напряжения, определяемые отношением силы к единице площади [Па]. Если в поп. сечении выделить элемент DА, к которому будет приложена сила DР, то DР/DА=рm – среднее полное напряжение в рассматриваемой точке поперечного сечения. 





ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТУПЕНЧАТЫХ БРУСЬЯХ С НЕСКОЛЬКИМИ СИЛОВЫМИ УЧАСТКАМИ.
ОТВЕТ: Растяжением или сжатием бруса называют такой его вид деформации, при котором все внешние силы направлены по продольной оси, а в поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N. Ее величину определяют, используя метод сечений: 
ΔB=-qe 4 /8EIx +RBe 3 /3EIx =0 =>RB=3qe/8
2. Сравнение угловых перемещений.
Можно отбросить связь, препятствующая повороту опорного сечения А и записать
Также ур-е деформации слагаемое означает углы поворота.
изучаем сопротивление материалов
Деформация
Перемещение — изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки. Полное перемещение точки в пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.
Деформация — изменение формы и размеров тела.
Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают также в себя перемещения как жесткого целого ненагруженных областей. Поэтому перемещения не могут характеризовать степень деформирования в окрестности рассматриваемой точки. Для этого используют понятие деформации. В отдельных случаях их величины могут совпадать (растяжение стержня), но в общем случае — это разные вещи.
Остановимся еще на одном важном моменте. Очень часто путают два понятия — «деформация» и «перемещение» — хотя ясно, что они не адекватны. Например, представим себе канат, прикрепленный к потолку. По канату на некоторую высоту поднялся человек. Очевидно, что под действием веса человека (пренебрегая весом каната) деформируется (растягивается) только верхняя часть каната, заключенная между потолком и местом, где находится человек. Нижняя часть каната не деформируется, а перемещается как твердое тело. Следовательно, не всегда перемещения сечений какого-то участка стержня непосредственно связаны с его деформацией.
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. 3-е изд. — М.: Высшая школа, 2003.
Деформации могут быть угловые и линейные.
Линейная деформация характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.
Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига.
Полная деформация — это сумма линейной и угловой деформации.
Если взять малый элемент тела параллелепипед, ориентированный по осям x, y, z, то соответственно возникает три линейных деформации (вдоль осей x, y, z ) εx,εy, εz
$$\epsilon _x = <Δdx\over dx>, \quad \epsilon _y = <Δdy\over dy>,\quad \epsilon _z = <Δdz\over dz>$$
и три угловые деформации [math]\gamma _
Относительные линейные и угловые деформации – величины безразмерные.
Деформации упругие и пластические
Деформации делятся на упругие и пластические (остаточные).
Типы деформаций
В зависимости от приложенных к телу нагрузок различают несколько видов деформации, отличающиеся законом распределения напряжений по сечению тела.
Растяжение-сжатие в поперечном сечении действует только одно внутреннее усилие, не равное нулю — продольное усилие. Конструкция В этом случае говорят о линейной деформации конструкции (характеризуется абсолютным и относительным удлинением, остальными деформациями пренебрегают). Чистый сдвиг в поперечном сечении действует только поперечная сила. В этом случае линейные относительные деформации равны нулю, углы сдвига не равны нулю (характеризуется изменением формы) Кручение в поперечном сечении действует только крутящий момент. Линейные относительные деформации равны нулю, углы сдвига не равны нулю. Изгиб в поперечном сечении действуют изгибающий момент и поперечная сила. Сложное сопротивление одновременное действие нескольких типов простых деформаций — растяжения-сжатия, кручения, изгиба.
Для каждого из указанных видов деформации существуют свои формулы для расчета на прочность.
Деформации и перемещения
Основные положения курса СМ
Сопротивление материалов – наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и машин.
Прочность – способность конструкции выдерживать определенную нагрузку, не разрушаясь.
Жесткость – способность конструкции сопротивляться изменению своих первоначальных размеров и формы под действием внешних нагрузок.
Устойчивость – способность конструкции сохранять определенную начальную форму упругого равновесия.
Для того чтобы конструкции в целом отвечали требованиям прочности, жесткости и устойчивости, необходимо придать их элементам наиболее рациональную форму и определить соответствующие размеры.
Основная задача СМ – это определение размеров и формы элементов конструкций, обеспечивающих их прочность и надежную работу при условии наименьшего расхода материала.
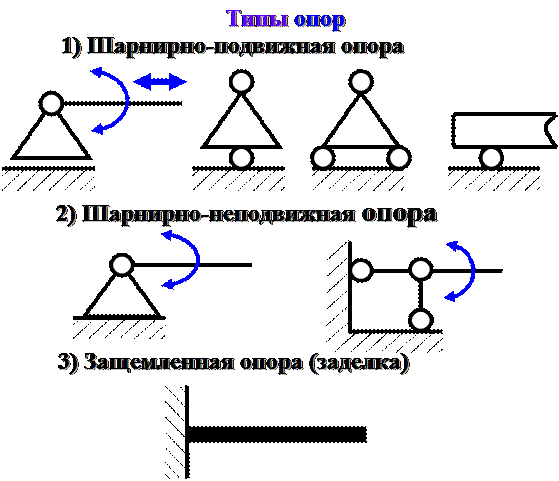
В СМ преимущественно рассматривают стержни постоянного сечения, которые в расчетных схемах изображают одной осевой линией с идеализированными опорами.
Внешние силы (нагрузки)
Внешними силами или нагрузками, называются силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.
а) по способу приложения на:
1) сосредоточенные – силы приложенные в точке (силы, которые передаются через площадку небольших размеров по сравнению с размерами всего элемента). Характеристикой является модуль силы F (Н).
по длине – характеристика интенсивность q (Н/м);
б) по характеру действия на:
1) статические – постоянные во времени;
2) динамические – изменяющиеся во времени.
Деформации и перемещения
Под действием внешних сил, все тела изменяют свои размеры и форму вплоть до разрушения. Это изменение называется деформация.
Основными типами простых деформаций являются:
1. Растяжение или сжатие;
2. Сдвиг или срез (перерезывание, работа заклепок);
3. Кручение (работа валов);
4. Изгиб (работа балок).
Появление в телах сразу нескольких простых деформаций приводит к сложным видам деформаций, например, изгиб с кручением.
Зная деформации и условия закрепления тела, можно определить перемещения всех точек тела, т.е. указать их положение после деформации.
Дата добавления: 2015-12-16 ; просмотров: 2753 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ



Напряжения
Основные виды деформаций.
Метод сечения для определения внутренних усилий.
Деформации и перемещения.
Все тела под действием приложенных к ним внешних сил в той или иной степени деформируются, т.е. изменяют свои размеры или форму либо и то и другое одновременно.
Изменение линейных размеров тела илиего частей называетсялинейной, а изменение угловых размеров —угловой деформациями.
При этом увеличение размеров тела называетсяудлинением, а уменьшение размеров — укорочением.
Если деформации изменяются по объему тела, то говорят о деформации вданной точке тела, в определенном направлении.
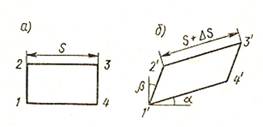
Если на поверхности тела, вблизи исследуемой точки, нанести весьма малый прямоугольник 1234 (рис. 5, а), то в результате деформации этот прямоугольник в общем случае Примет вид параллелограмма 1 ’ 2′ 3′ 4′ (рис. 5, б).
Длины сторон прямоугольника изменятся (увеличатся или уменьшатся), а стороны повернутся по отношениюкпервоначальному положению.
Если, например, длинастороны 23изменится на величину ∆s, то отношение
называетсясредней относительной деформацией (в данном случае средним удлинением) в точке 2.
При уменьшении отрезка ε в пределе получим,
где величина ε называетсяистинной относительной деформацией в точке 2 в направлении 23.
Изменение первоначального прямого угла между сторонами рассматриваемого прямоугольника γ=α+β будет характеризовать угловую деформацию (или угол сдвига) в данной точке.
Опыт показывает, что деформации, как линейные, так и угловые, могут после снятия нагрузки или полностью исчезнуть, или исчезнуть лишь частично (в зависимости от материала и величины нагружения).
Деформации, исчезающие после разгрузки тела, называются упругими, а свойство тел принимать послеразгрузки своюпервоначальную форму называетсяупругостью.
Деформации же, сохраняемые телом и после удаления нагрузки, называютсяостаточными илипластическими, а свойство материалов давать остаточные деформации называетсяпластичностью.
Зная деформации телаво всех его точках и условия закрепления, можно определитьперемещения всех точек тела, т. е. указать их положение (новые координаты) после деформации. Для нормальной эксплуатации сооружения деформации его отдельных элементов должны быть, как правило, упругими, а вызванные ими перемещения не должны превосходить по величине определенных допускаемых значений. Эти условия, выраженные в форме тех или иных уравнений, называются условиямижесткости. В некоторых случаях допускаются небольшие пластические деформации (для конструкций из железобетона, пластмасс и для конструкцийиз металла при действии высоких температур).
Понятия о перемещениях и деформациях
Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.
Ответ:
Жёсткость – это способность тела или конструкции сопротивляться деформации.
Ответ:
Формулу удельной потенциальной энергии изменения формы получим из формулы полной удельной потенциальной энергии деформации (3.5), подставляя значение коэффициента Пуассона равного ν=0,5.
Условие прочности имеет вид


Третья и четвертая теории прочности дают удовлетворительное совпадение результатов теоретического расчета с опытными данными для пластичных материалов и широко применяются при расчетах на прочность. Для хрупких материалов эти теории не применимы.
Билет №10.
Ответ:
Растяжением или сжатием называют такой вид деформации бруса (стержня), при котором в его поперечных сечениях возникает только продольная сила N.
Продольная сила, направленная от сечения, связана с растяжением и считается положительной; сила, направленная к сечению; связана со сжатием и считается отрицательной.
При расчёте стержня на прочность необходимо знать значения внутренних силовых факторов во всех его сечениях. Для этого строят график (эпюру), показывающий, как изменяется внутренний силовой фактор (сила или момент) по длине стержня.
Ответ:
Системы, для которых все реакции связей могут быть определены с помощью уравнений равновесия, называются статически определимыми.
Системы, для которых количество реакций связей превышает число возможных уравнений равновесия, называются статически неопределимыми системами.
Разность между числом неизвестных и числом независимых уравнений равновесия определяет степень статической неопределимости.
Дополнительные уравнения, называемые уравнениями совместности перемещений, составляют, определяя перемещения отдельных стержней системы и устанавливая между ними связь.
Ответ:
Теория прочности Мора не содержит критериальных гипотез и основана в первую очередь на логической систематике экспериментальных результатов. Её основное допущение заключается в том, что главное напряжение 


где 
Для хрупких материалов отношение 

Условие прочности запишется в виде:

Наилучшие результаты эта теория даёт для случая, когда 


Билет №11.
Ответ:
. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми. Основные соотношения, полученные для них, приведены в таблице 7.1
| Виды нагружения | Напряжения | Деформации |
| Растяжение |  . Условие прочности: . Условие прочности:  |  |
| Изгиб |  . Условие прочности: . Условие прочности:  |  |
| Кручение |  . Условие прочности: . Условие прочности:  |  |
Кроме простых видов нагружения бывают и сложные виды нагружения или иначе сложное сопротивление.
Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.
Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:
При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.
Ответ:
При эксплуатации конструкции возможно изменение температуры, вызванное условиями работы или сменой времен года. С изменением температуры изменяются линейные размеры элементов конструкции: увеличиваются при нагреве, уменьшаются при охлаждении на величину 




В статически определимых системах длина стержня может свободно изменяться при их нагреве или охлаждении.
В статически неопределимых системах при изменении температуры возникают дополнительные силы. Если нагреть стержень, жёстко закреплённый по концам, то его длина не может изменяться: этому препятствуют жёсткие заделки. В опорах (заделках) возникают реакции, сжимающие стержень.
Ответ:
Критерии прочности и пластичности, рассмотренные в предыдущих параграфах, справедливы для традиционных конструкционных материалов — однородных и изотропных. Однако в последнее время в различных областях техники, в том числе и в строительстве, все большее распространение получают новые, так называемые композиционные материалы (композиты). Композит представляет собой полимерную или металлическую матрицу, армированную высокопрочными волокнами (стеклянными, угольными и т. п.). Отличительными признаками этих материалов являются их неоднородность и, как правило, ярко выраженная анизотропия свойств. Последнее обстоятельство находит отражение, в том числе и в прочностных свойствах композитов.
Армирование композита может быть однонаправленным (рис. 14.9, а), ортогональным (рис. 14.9, б), симметричным в нескольких направлениях (рис. 14.9, в).
Рис. 14.9. Схемы армирования композитов
При однонаправленном армировании прочность материала в направлении армирования высокая, а в ортогональном направлении значительно меньше, потому что определяется в основном прочностью матрицы.
Если подвергнуть однонаправленный композит испытанию на растяжение или на сдвиг, то разрушение может произойти частично за счет разрыва волокон, а частично за счет скалывания матрицы. Аналогичные соображения оказываются справедливыми и в общем случае армирования композиционных материалов волокнами.
Условие прочности композита можно записать в следующем виде:

В настоящее время известно большое число различных критериев прочности, предложенных для новых конструкционных материалов. В частности, один из критериев прочности для ортотропных материалов представляет собой обобщение критерия текучести по удельной энергии формоизменения и в случае плоского напряженного состояния записывается следующим образом:

где 

Если материал имеет разные пределы прочности при растяжении и сжатии, то могут быть использованы условия прочности вида


Константы, фигурирующие в этих соотношениях, определяются из опытов на растяжение, сжатие и сдвиг.
Следует обратить внимание на то, что результаты испытаний композитов обладают очень большим случайным разбросом и потому указанные константы должны находиться лишь на основе статистического анализа. Последнее обстоятельство тем более затрудняет выбор наилучшего критерия прочности композиционного материала.
Среди композитов, применяемых в строительстве, наибольшее распространение имеют всевозможные полимерные материалы, на прочность которых оказывают большое влияние многие факторы, среди которых в первую очередь нужно назвать температуру и время. Например, увеличение температуры всего на 20. 30°C приводит к заметному снижению прочности указанных материалов. Еще более существенным при оценке прочности их является учет временного фактора. Обсуждению этого вопроса посвящена гл. 16.
Билет №12.
Ответ:
Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.
Ответ:
Разность между числом неизвестных и числом независимых уравнений равновесия определяет степень статической неопределимости.
Системы, для которых количество реакций связей превышает число возможных уравнений равновесия, называются статически неопределимыми системами.
Ответ:
Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты.
Изгиб называется плоским, если плоскость действия момента проходит через главную центральную ось инерции сечения.
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы 
Брус, работающий при изгибе, называется балкой.
Билет №13.
Ответ:
Внутри любого материала имеются внутренние межатомные силы. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) их, т.е. появление дополнительных внутренних сил. Дополнительные силы взаимодействия, возникающие внутри объекта под действием внешних сил, называются в сопротивлении материалов внутренними силами.
Для определения внутренних усилий используется метод сечений.
Существует шесть составляющих, которые называются внутренними силовыми факторами (В.С.Ф):
Qx, Qy — поперечные силы, проекции вектора R на оси x, y соответственно;
Mx, My — изгибающие моменты, составляющие момента M вокруг осей x, y соответственно.
Ответ:
Определим величины нормальных и касательных напряжений, действующих в площадках повернутых под углом 45 о к главным. Из формул (3.1) получим, что
Экспериментально установлено, что существует линейная зависимость между углом сдвига g и касательными напряжениями t (рис.3.11), являющейся законом Гука при сдвиге

где G – модуль сдвига, характеризующий способность материала сопротивляться сдвиговой деформации, т.е. характеризующая жесткость материала при сдвиге.
Величина модуля сдвига связана с модулем упругости при растяжении Е и коэффициентом Пуассона ν соотношением
Упругостью называется свойство тел восстанавливать свои первоначальные форму и размеры после снятия нагрузки.

Ответ:
Существует шесть составляющих, которые называются внутренними силовыми факторами (В.С.Ф):
Qx, Qy — поперечные силы, проекции вектора R на оси x, y соответственно;
Mx, My — изгибающие моменты, составляющие момента M вокруг осей x, y соответственно.
Билет №14.
Ответ:


При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах

Ответ:
Рассмотрим основы практических расчетов на срез заклепочных соединений. Более подробно эти вопросы освещаются в курсах деталей машин и конструкций. На рис. 5.5 показано соединение двух листов заклепками (соединение внахлестку). Соединение разрушается в результате перерезывания заклепок по линии соприкосновения листов. Если разрушение каждой заклепки происходит по одной плоскости среза, то заклепочное соединение называется односрезным, если по двум плоскостям, то соединение называется двухсрезным и т.д.
Учитывая большие трудности, связанные с определением действительного напряженного состояния материала заклепки в зоне разрушения, для упрощения задачи принимаем, что по плоскостям среза действуют только касательные напряжения, которые распределяются по поверхности среза равномерно. Второе допущение устанавливает, что при действии статической нагрузки можно принимать поперечную силу в каждой заклепке равной
Приняв указанные допущения, получим условие прочности заклепок на срез:
Условие прочности на смятие имеет следующие вид:
В случае склепывания внахлестку двух листов различной толщины надо принимать t=tmin.
Кроме расчета на срез и смятие составляют также условие прочности листа на разрыв
Ответ:
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым.
Определим нормальные напряжения, возникающие при чистом изгибе балки находящейся под действием моментов Мх.
В произвольной точке балки (рис.6.6, т.А) в общем случае могут возникать нормальные напряжения как вдоль продольной оси σz, так и вдоль поперечных осей σx, σy. Однако экспериментально установлено, что нормальные напряжения σx, σy пренебрежимо малы по сравнению с напряжениями σz. Принимается так называемая гипотеза ненадавливания продольных волокон σx = 0, σy = 0. Поэтому можно принять, что материал балки находится при линейном напряженном состоянии вдоль оси z, и деформации подчиняются закону Гука. То есть нормальные напряжения при изгибе можно определить из формулы 
Установим закон изменения деформаций при изгибе балки. Экспериментально получено, что в деформируемой балке поперечные сечения плоские до деформации остаются плоскими и поперечными после деформации, имеет место гипотеза плоских сечений. При этом верхние волокна удлиняются, нижние укорачиваются, а продольная линия не меняет своей длины. Слой балки, не испытывающий при изгибе ни растяжения ни сжатия, называется нейтральным слоем. Линия пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией.


Подставляя это соотношение в закон Гука, получим:

т.е. напряжения s линейно зависят от координаты у.
Используя интегральную связь между напряжениями и изгибающим моментом

подставляя в него соотношение (6.1), получим 

Тогда получим выражение 

Эпюра нормальных напряжений показана на рис.6.6. Как видно, на нейтральной линии они равны нулю, максимального значения напряжения достигают в крайних верхних и нижних волокнах балки.

Обозначая 

где Wx – осевой момент сопротивления сечения изгибу, геометрическая характеристика поперечного сечения.
Билет №15.
Ответ:
Нормальные и касательные напряжения в каждом поперечном сечении тела связаны определенным образом с внутренними усилиями, действующими в этом сечении. Если рассмотреть элементарную площадку dF поперечного сечения F бруса с действующими по этой площадке напряжениями s, tх, tу, получим, что на площадку dF действуют элементарные силы s dF, tхdF tуdF. Тогда можно записать следующие интегральные зависимости:
Ответ:
Исходя из принципа равнопрочности сварного стыка и основного металла, а также принимая во внимание, что сварное соединение весьма часто разрушается по основному металлу, нормативное сопротивление (предел текучести) сварного соединения принимают таким же, как для основного металла.
Одинаковыми с основным металлом принимаются и коэффициенты однородности для соединений стыковыми швами, выполненных автоматической сваркой. В случае ручной сварки шлакообразующими электродами коэффициенты однородности соединений в стык в растянутых элементах принимаются одинаковыми с основным металлом только при плотных швах, плотность которых гарантирована специальными мерами контроля над качеством швов; последнее обязательно для ответственных конструкций, особенно работающих на динамическую нагрузку, Если отсутствует специальный контроль, то ввиду большого рассеяния величин прочности сварки для стыковых швов, работающих на растяжение, коэффициент однородности принимается более низкий, чем для основного металла (порядка 0,75). Для сжатых элементов, где небольшая пористость швов не имеет существенного значения, величины коэффициентов однородности принимаются такими же, как для основного металла. В результате для расчета соединений в стык, выполненных ручной сваркой шлакообразующими электродами, получаются два расчетных сопротивления осевым усилиям, равных для конструкций из малоуглеродистой стали: 

Расчетное сопротивление срезу принимается при расчете соединений в стык таким же, как для основного металла: 

Ответ:
Жёсткость – это способность тела или конструкции сопротивляться деформации.
Кривизна нейтрального слоя изогнутой оси балки прямо пропорциональна изгибающему моменту и обратно пропорциональна величине 
Формула выведена для чистого изгиба бруса, при котором во всех поперечных сечениях момент 
Билет №16.
Ответ:
Рассмотрим решение задачи об устойчивости сжатого стержня. Пусть стержень, оба конца которого закреплены шарнирно, сжат силой Ркр (рис.9.2). Стержень искривился так, что в сечении z прогиб составил δ. Приближенное дифференциальное уравнение изогнутой оси балки имеет вид:


Изгибающий момент в сечении z в изогнутом состоянии равен моменту силы Ркр, но обратного направления, а, следовательно, и знака

Тогда дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости будет

Обозначая 

Его общее решение имеет вид

где С и D – постоянные интегрирования, определяемые из условий на опорах. На опорах стержня прогиб равен нулю, т.е. 1) при z=0, δ=0;
2) при z=l, δ=0. Подставляя первое условие в уравнение прогибов получим С=0, из второго условия получим 
Последнее соотношение справедливо при 
Откуда 

Минимальное действительное значение критической силы получится при n=1

Это и есть формула Эйлера для критической силы.
Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной

Ответ:
Удельной потенциальной энергией деформации u называется величина потенциальной энергии деформации U, накопленной в единице объема тела V. Для линейного напряженного состояния:

Используя принцип независимости действия сил, полученный результат можно обобщить на случай объемного напряженного состояния:

В случае площадок общего положения (не главных площадок) выражение для удельной потенциальной энергии приобретает вид:

Предыдущее выражение можно преобразовать с помощью формул обобщенного закона Гука к виду:
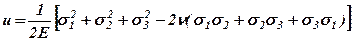
Рассмотрим напряженное состояние чистого сдвига. Запишем выражение удельной потенциальной энергии деформации по площадкам чистого сдвига:


Очевидно, величина удельной потенциальной энергии деформации u не должна зависеть от того по каким площадкам она записана, поэтому 

Таким образом, постоянные упругости материалов, характеризующие жесткость при растяжении и сдвиге и поперечную деформацию, являются зависимыми. Поэтому достаточно определить лабораторным путем при растяжении две характеристики упругости Е и n, а третья G может быть вычислена аналитически.