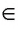Что такое взаимное расположение точек на прямой

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

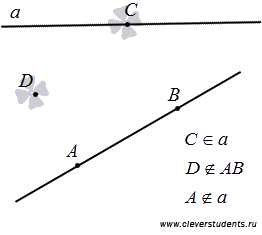
Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

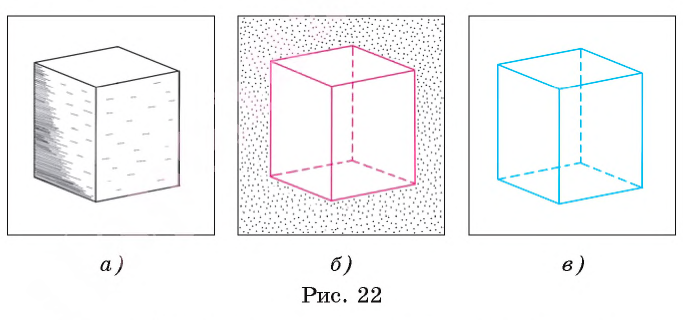
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 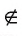b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

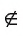
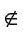
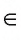
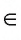
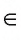
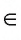
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

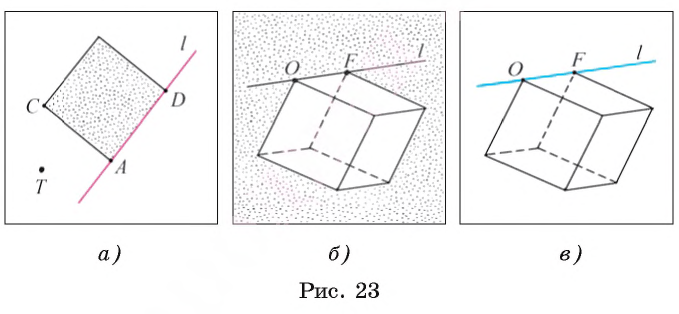
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

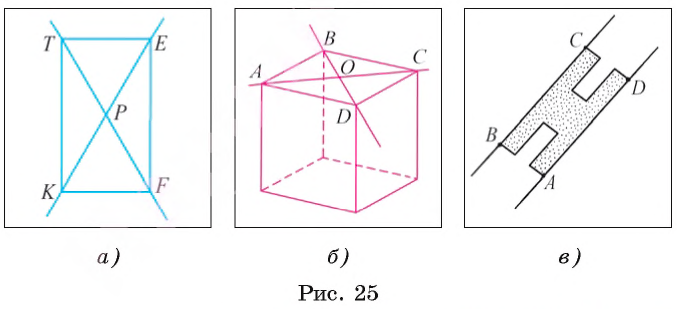
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 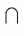ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 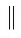l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС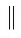АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Взаимное расположение прямой и точки

Прямая на плоскости – необходимые сведения.

В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.

Навигация по странице.

Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).

Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.

Теперь можно переходить и к понятию прямой линии на плоскости.

Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Точки принято обозначать большими латинскими буквами, например, точки А и F. В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d.

Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

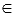
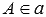
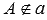
Для обозначения принадлежности точки некоторой прямой используют символ « ». К примеру, если точка А лежит на прямой а, то можно записать . Если точка А не принадлежит прямой а, то записывают .

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком. Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА. Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».

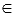
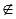
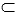
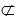
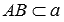
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а, можно кратко записать .

Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А, В и С лежат на одной прямой, причем точка В лежит между точками А и С. Тогда можно говорить, что точки А и С находятся по разные стороны от точки В. Также можно сказать, что точки В и С лежат по одну сторону то точки А, а точки А и В лежат по одну сторону от точки С.

Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – двалуча. Для этого случая дается аксиома: произвольная точка О, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точкиО, а две любые точки разных лучей – по разные стороны от точки О.

Источник

Прямая на плоскости – необходимые сведения.

В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.

Навигация по странице.

Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).

Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.

Теперь можно переходить и к понятию прямой линии на плоскости.

Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В ), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА ).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Взаимное расположение прямых на плоскости.

Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?

Во-первых, две прямые на плоскости могут совпадать.

Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.

Во-вторых, две прямые на плоскости могут пересекаться.

В-третьих, две прямые на плоскости могут быть параллельными.

Две прямые на плоскости называются параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение . Для более полной информации смотрите статью параллельные прямые, параллельность прямых.

Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой. В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.

Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой. О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости.

Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.

Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:

Способы задания прямой на плоскости.

Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.

Во-первых, прямую можно задать, указав две точки на плоскости.

Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.

Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки.

Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.

Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой.

В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.

Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости.

Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.

Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.

Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой.

Источник