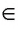Что такое взаимное расположение точек 7 класс

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

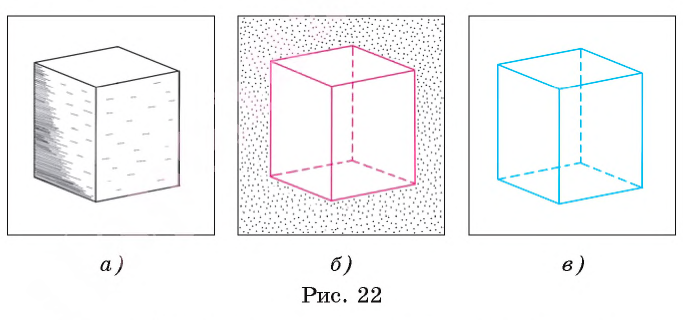
Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 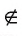b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

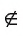
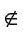
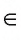
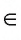
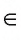
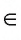
Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С l, Т l), проходящей через вершины А и D квадрата (А l, D l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O l, F l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

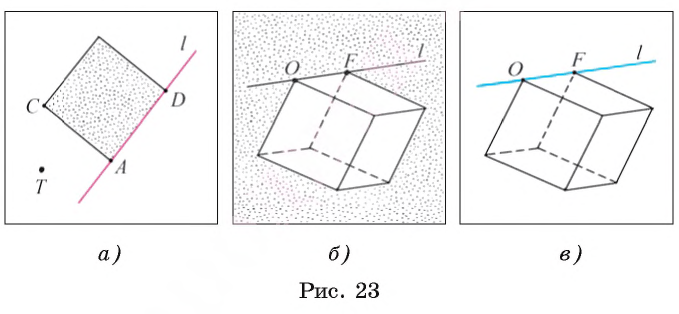
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

1 Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а b (читают: «Прямые а и b пересекаются в точке О»).

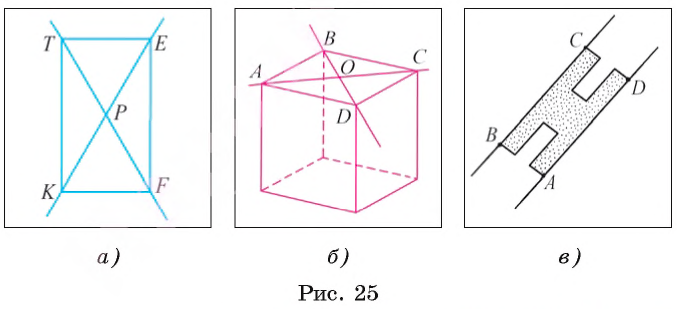
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 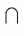ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁ 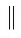l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС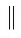АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник