Что такое высказывание математическая логика
Высказывание (логика)
Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание. Пример: A(x) = «В городе x идёт дождь.», где A — высказывательная форма, x — объект.
Содержание
Виды высказываний
Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.
Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.
Элементарные логические высказывания — это высказывания не относящиеся к составным.
Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».
Связь с математической логикой
Обычная логика двухзначна, то есть приписывает высказываниям только два возможных значения: истинно оно или ложно.
Пусть 


Тождественно истинное высказывание обозначают символом 1, тождественно ложное — символом 0.
Основные операции над логическими высказываниями
Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.
Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Кванторное логическое высказывание с квантором всеобщности (
Кванторное логическое высказывание с квантором существования (
См. также
Примечания
Литература
Полезное
Смотреть что такое «Высказывание (логика)» в других словарях:
Высказывание — Высказывание: Высказывание (логика) предложение, которое может быть истинно или ложно. Высказывание (лингвистика) предложение в конкретной речевой ситуации. См. также Суждение … Википедия
ЛОГИКА — (от греч. logos слово, понятие, рассуждение, разум), или Формальная логика, наука о законах и операциях правильного мышления. Согласно основному принципу Л., правильность рассуждения (вывода) определяется только его логической формой, или… … Философская энциклопедия
ЛОГИКА ВЫСКАЗЫВАНИЙ — раздел логики, в котором изучаются истинностные взаимосвязи между высказываниями. В рамках данного раздела высказывания (пропозиции, предложения) рассматриваются только с т.зр. их истинности или ложности, безотносительно к их внутренней субъектно … Философская энциклопедия
логика высказываний — ЛОГИКА ВЫСКАЗЫВАНИЙ, пропозициональная логика раздел символической логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения. В отличие от логики предикатов, простые высказывания при этом выступают как… … Энциклопедия эпистемологии и философии науки
ВЫСКАЗЫВАНИЕ — грамматически правильное повествовательное предложение, взятое вместе с выражаемым им смыслом. В логике употребляется несколько понятий В., существенно различающихся между собой. Прежде всего это понятие дескриптивного, или о п и с а тельного,… … Философская энциклопедия
Логика Бэрроуза — Логика Бэрроуза Абади Нидхэма (англ. Burrows Abadi Needham logic) или BAN логика (англ. BAN logic) это формальная логическая модель для анализа знания и доверия, широко используемая при анализе протоколов… … Википедия
ЛОГИКА ПРЕДИКАТОВ — центральный раздел логики, в котором изучается субъектно предикатная структура высказывании и истинностные взаимосвязи между ними. Л.п. представляет собой содержательное расширение логики высказываний. В рамках данного раздела любое высказывание… … Философская энциклопедия
ЛОГИКА НАУЧНОГО ПОЗНАНИЯ — или Логика науки, применение идей, методов и аппарата логики в анализе научного познания. Развитие логики всегда было тесно связано с практикой теоретического мышления и прежде всего с развитием науки. Конкретные рассуждения дают логике материал … Философская энциклопедия
ЛОГИКА СИМВОЛИЧЕСКАЯ — ЛОГИКА СИМВОЛИЧЕСКАЯ математическая логика. теоретическая логика область логики, в которой логические выводы исследуются посредством логических исчислений на основе строгого символического языка. Термин “символическая логика” был, по видимому … Философская энциклопедия
ЛОГИКА НАУКИ — в спец. смысле дисциплина, применяющая понятия и технич. аппарат совр. формальной логики к анализу систем науч. знания. Термин «Л. н.» часто употребляется также для обозначения законов развития науки (логика науч. развития), правил и… … Философская энциклопедия
Знания за пределами математики и доказательной логики состоят из предположений. Предположения, составляющие математические знания, закрепляются доказательными рассуждениями и подкрепляются правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, косвенные улики юриста, индуктивные доводы физика, статистические доводы экономиста относятся к правдоподобным рассуждениям. Доказательное рассуждение надежно, неоспоримо, окончательно. Правдоподобное рассуждение рискованно, спорно, условно.
Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой, являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи и нет никакой теории таких рассуждений, которая могла бы сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.
Доказательные рассуждения. Все новые знания о мире связаны с правдоподобными рассуждениями.
Часто математические утверждения касаются бесконечного множества объектов, и перебрать эти объекты невозможно. Такой перебор можно заменить следующим методом рассуждения: если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае, а значит и во всех случаях. Такой метод рассуждения называется методом математической индукции.
Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Обобщение часто делается при переходе от одного предмета к целому классу, содержащему этот предмет.
Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Специализация часто производится при переходе от целого класса предметов к одному предмету, содержащемуся в этом классе.
Аналогия. Две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей. Это отношение имеет ясный смысл, если отношения управляются одними и теми же законами.
Далее приводятся некоторые основные факты математической логики, которую еще называют формальной логикой. Формальной потому, что она позволяет проверить правильность рассуждений независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.
Высказывания и логические связки
Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ V, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было. » и т.д., а символ
Отрицание — это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание можно обозначать по-разному: 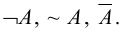
Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях
требуется «перевод» полученного высказывания на русский язык. Пусть, например, А = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания А является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.
Отрицанием 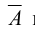
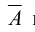
Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция A v В истинна, когда истинно, по крайней мере, одно из высказываний А и В или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.
Импликация образуется из высказываний А и В с помощью слов «если. то. ». Получается высказывание вида «если А то В». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.
На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если А, то В» предполагает между А и В отношение посылки и следствия, или же причины и обусловленного ею действия.
Импликация обозначается 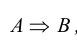
Договорились, что импликация 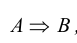
Эквиваленция образуется из высказываний А и В с помощью слов «. тогда и только тогда, когда. »:
Утверждение «А тогда и только тогда, когда В» не означает в логике, что составляющие высказывания А и В имеют одно и то же значение или один и тот же смысл.
Эквиваленция обозначается 
Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.
В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.
Лекции по предметам:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что такое высказывание математическая логика
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предложение «Соблюдайте правила техники безопасности в компьютерном классе» высказываниями не являются. Повествовательные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство является внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются высказываниями, поскольку это суждения, о каждом из которых можно сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».
Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логическими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве которых используются заглавные латинские буквы. Логические переменные могут принимать только одно из двух возможных значений: «истина» или «ложь». Например, высказывание «Информация в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Принтер является устройством хранения информации» можно обозначить логической переменной В. Поскольку первое высказывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказывание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Логическое отрицание простого высказывания получают добавлением слов «Неверно, что» в начале простого высказывания.
■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы умеют летать». Результатом логического отрицания будет высказывание «Неверно, что крокодилы умеют летать». Значение исходного высказывания — «ложь», а значение нового — «истина».
■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказывание «Неверно, что файл должен иметь имя». Значение исходного высказывания — «истина», а значение нового высказывания — «ложь».
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
■ ПРИМЕР 3. Имеются два простых высказывания. Одно высказывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение нового сложного высказывания также «ложь».
■ ПРИМЕР 4. Имеются два простых высказывания. Первое высказывание — «Карлсон живет в подвале». Второе высказывание — «Карлсон лечится вареньем».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».
■ ПРИМЕР 5. Имеются два простых высказывания. Первое высказывание — «Карлсон живет на крыше». Второе высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
Логика высказываний: теория и применение. Примеры решений задач
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Логика высказываний: определение и применение
Высказываниями принято считать такие предложения (написанные на «словесном» либо математическом языке), о которых можно сказать одно из двух: либо они являются истинными, либо ложными.
С математическими высказываний проще всего: они всегда имеют либо значение «истина», либо значение «ложь». Для высказываний, сделанных на «словесном» языке, понятия «истинности» и «ложности» несколько более расплывчаты. Однако, например, такие словесные формы, как «Иди домой» и «Идёт ли дождь?», не являются высказываниями. Поэтому понятно, что высказываниями являются такие словесные формы, в которых что-либо утверждается. Не являются высказываниями вопросительные или восклицательные предложения, обращения, а также пожелания или требования. Их невозможно оценить значениями «истина» и «ложь».
Логика высказываний отвлекается от содержательной нагрузки высказываний и изучает их истинностное значение, то есть является ли высказывание истинным или ложным.
Логические операции над высказываниями
Итак, высказывания можно рассмотривать как величину, которая может принимать два значения: «истина» и «ложь».
Таблица истинности для конъюнкции:
| A | B | A ∧ B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Таблица истинности для дизъюнкции:
| A | B | A ∨ B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Таблица истинности для следования (импликации):
| A | B | A → B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
4. Четвёртая логическая операция над высказываниями, точнее над одним высказыванием, называется отрицанием высказывания A и обозначается
A (можно встретить также употребление не символа
, а символа ¬, а также верхнего надчёркивания над A).
A есть высказывание, которое ложно, когда A истинно, и истинно, когда A ложно.
Таблица истинности для отрицания:
Таблица истинности для эквивалентности:
| A | B | A → B | B → A | A ↔ B |
| И | И | И | И | И |
| И | Л | Л | И | Л |
| Л | И | И | Л | Л |
| Л | Л | И | И | И |
В большинстве языков программирования есть специальные символы для обозначения логических значений высказываний, записываются они почти во всех языках как true (истина) и false (ложь).
Подытожим вышесказанное. Логика высказываний изучает связи, которые полностью определяются тем, каким образом одни высказывания строятся из других, называемых элементарными. Элементарные высказывания при этом рассматриваются как целые, не разложимые на части.
Систематизируем в таблице ниже названия, обозначения и смысл логических операций над высказываниями (они нам вскоре вновь понадобятся для решения примеров).
Для логических операций верны законы алгебры логики, которые можно использовать для упрощения логических выражений. При этом следует отметить, что в логике высказываний отвлекаются от смыслового содержания высказывания и ограничиваются рассмотрением его с той позиции, что оно либо истинно, либо ложно.
Пример 1. Вычислите логические значения следующих высказываний:
3) («Сосна» = «Дуб») ИЛИ («Вишня» = «Клён») ;
6) («Глаза даны, чтобы видеть») И («Под третьим этажом находится второй этаж») ;
Пример 2. Запишите с помощью логических операций следующие сложные высказывания:
1) «Пользователь не зарегистрирован»;
2) «Сегодня воскресенье и некоторые сотрудники находятся на работе»;
3) «Пользователь зарегистрирован тогда и только тогда, когда отправленные пользователем данные признаны годными».
Решить примеры на логику высказываний самостоятельно, а затем посмотреть решения
Пример 3. Вычислите логические значения следующих высказываний:
1) («В минуте 70 секунд») ИЛИ («Работающие часы показывают время») ;
2) (28 > 7) И (300/5 = 60) ;
4) Не((300 > 100) ИЛИ («Жажду можно утолить водой»)) ;
Пример 4. Запишите с помощью логических операций следующие сложные высказывания и вычислите их логические значения:
1) «Если часы неправильно показывают время, то можно невовремя прийти на занятия»;
Пример 5. Определите логическое значение выражения
Формулы логики высказываний
Понятие логической формы сложного высказывания уточняется с помощью понятия формулы логики высказываний.
В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания. Вообще-то они называются формулами логики высказываний.
Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы
Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее называть их элементарными формулами или атомами.
Для построения формул логики высказываний кроме указанных выше букв используются знаки логических операций
Понятие формулы логики высказываний определим следуюшим образом:
1) элементарные формулы (атомы) являются формулами логики высказываний;
3) только те выражения являются формулами логики высказываний, для которых это следует из 1) и 2).
Определение формулы логики высказываний содержит перечисление правил образования этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется из атомов в результате последовательного применения правила 2).
1) 
2) 
3) 
4) 
5) 
6) 
1) «нет действительных чисел, которые являются рациональными»;
2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;
5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;
6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».
| p | q | r |  |  |  |  | f |
| И | И | И | И | И | И | И | И |
| И | И | Л | И | И | И | Л | И |
| И | Л | И | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | Л | И | И |
| Л | И | И | Л | И | Л | И | И |
| Л | И | Л | Л | И | Л | И | Л |
| Л | Л | И | И | И | И | И | И |
| Л | Л | Л | И | И | И | Л | И |
Заметим, что никакой атом не имеет вида
Число скобок в формулах логики высказываний можно уменьшить, если принять, что
1) в сложной формуле будем опускать внешнюю пару скобок;
2) упорядочим знаки логических операций «по старшинству»:
В этом списке знак ↔ имеет самую большую область действия, а знак
— самую маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака
(при этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.
Пример 8. Восстановите скобки в формуле логики высказываний B ↔
Решение. Скобки восстанавливаются пошагово следующим образом:
Не всякая формула логики высказываний может быть записана без скобок. Например, в формулах А → (B → C) и
(A → B) дальнейшее исключение скобок невозможно.
Тавтологии и противоречия
Так как истинность или ложность сложных высказываний зависит лишь от значений, а не от содержания высказываний, каждому из которых соответствует определённая буква, то проверку того, является ли данное высказывание тавтологией, можно подставить следующим способом. В исследуемом выражении на место букв подставляются значения 1 и 0 (соответственно «истина» и «ложь») всеми возможными способами и с использованием логических операций вычисляются логические значения выражений. Если все эти значения равны 1, то исследуемое выражение есть тавтология, а если хотя бы одна подстановка даёт 0, то это не тавтология.
Таким образом, формула логики высказываний, которая принимает значение «истина» при любом распределении значений входящих в эту формулу атомов, называется тождественно истинной формулой или тавтологией.
Противоположный смысл имеет логическое противоречие. Если все значения высказываний равны 0, то выражение есть логическое противоречие.
Таким образом, формула логики высказываний, которая принимает значение «ложь» при любом распределении значений входящих в эту формулу атомов, называется тождественно ложной формулой или противоречием.
Кроме тавтологий и логических противоречий существуют такие формулы логики высказываний, которые не являются ни тавтологиями, ни противоречиями.
Пример 9. Составьте таблицу истинности для формулы логики высказываний 
Решение. Составляем таблицу истинности:
 |  |  |  |  |
| И | И | И | И | И |
| И | Л | Л | Л | И |
| Л | И | Л | И | И |
| Л | Л | Л | Л | И |
В значениях импликации не встречаем строку, в которой из «истины» следует «ложь». Все значения исходного высказывания равны «истине». Следовательно, данная формула логики высказываний является тавтологией.
Пример 10. Составьте таблицу истинности для формулы логики высказываний 
Решение. Составляем таблицу истинности:
 |  |  |  |  |  |
| И | И | И | И | И | И |
| И | И | Л | И | Л | Л |
| И | Л | И | Л | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | Л | И | И |
| Л | И | Л | Л | Л | И |
| Л | Л | И | Л | И | И |
| Л | Л | Л | Л | Л | И |
Как видно ниже, таблица истинности для такой замещающей логической операции идентична таблице истинности для импликации.
 |  |  |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Пример 11. Перепишите формулу логики высказываний 



Заменяем импликацию между двумя парами скобок, отрицая самый левый знак отрицания:

Убираем эквиваленцию между p и q и между q и не r :

Используя закон де Моргана, немного упрощаем и окончательно получаем:

Посылки и выводы. Валидный и не валидный аргумент
Пример валидного аргумента:
То есть, из посылок логически следует вывод.
Пример не валидного аргумента:
То есть, из посылок логически не следует вывод.
Пример 12. Проверьте валидность аргумента, если
Решение. Составляем таблицу истинности:
 |  |  |  |  |  |
| И | И | Л | И | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | И | И | Л |
| Л | Л | И | И | И | И |
Применение логики высказываний в информатике и программировании
Так, может быть объявлена логическая переменная с именем «ПользовательЗарегистрирован» (или его англоязычный аналог), имеющая форму высказывания, которой может быть присвоено логическое значение «истина» при выполнении условий, что данные для регистрации отправлены пользователем и эти данные программой признаны годными. В дальнейших вычислениях значения переменных могут меняться в зависимости от того, какое логическое значение («истина» или «ложь») имеет переменная «ПользовательЗарегистрирован». В других случах переменной, например, с именем «ДоДняХОсталосьБолееТрёхДней», может быть присвоено значение «Истина» до некоторого блока вычислений, а в ходе дальнейшего исполнения программы это значение может сохраняться или меняться на «ложь» и от значения этой переменной зависит ход дальнейшего исполнения программы.
Если в программе используются несколько логических переменных, имена которых имеют форму высказываний, и из них строятся более сложные высказывания, то намного проще разрабатывать программу, если перед её разработкой записать все операции с высказываний в виде формул, применяемых в логике высказываний, чем мы в ходе этого урока и займёмся.