Ортогональное проецирование прямой линии

4.1. Общие понятия и определения. Прямая в пространстве и на ортогональном чертеже может быть задана: а) двумя точками; б) точкой и направлением прямой; в) двумя пересекающимися плоскостями.

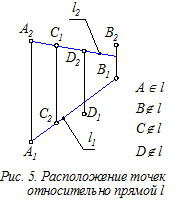
Определение. На эпюре точка лежит на прямой, если её проекции расположены на одноимённых проекциях этой прямой (рис. 5).

4.2. Расположение прямой относительно плоскостей проекций

В рассматриваемом разделе производится оценка проекционных свойств прямых в зависимости от их расположения относительно плоскостей проекции П₁, П₂ и П₃. При этом прямые в основном задаются лишь двумя своими проекциями (горизонтальной и фронтальной).

Прямая общего положения – это прямая, не перпендикулярная ни одной из плоскостей проекций (П₁, П₂ или П₃). Эпюрный опознавательный признак (ЭОП) прямых общего положения – обе заданные проекции прямых непараллельны и неперпендикулярны к координатным осям (рис. 6).

Проекционные свойства (ПС) прямых общего положения – длина прямых и углы их наклона к плоскостям проекций на ортогональном чертеже искажены, т. е. показаны не в натуральную величину.

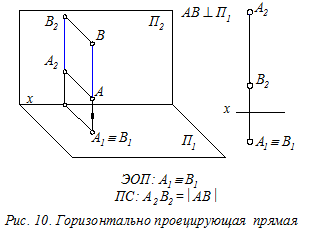
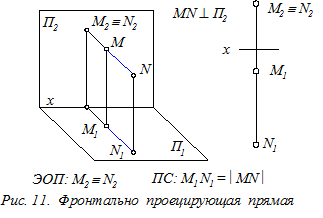
ЭОП прямых уровня: одна из заданных проекций прямой уровня параллельна координатной оси (0х или 0z). Это означает, что одна из трёх координат любой точки прямой уровня постоянна (т.е. не изменяется).

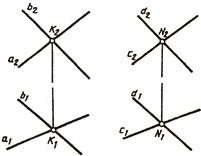
Определение. Вырожденной проекцией прямой называется точка ортогонального чертежа, где отобразились все точки этой прямой.

Вырожденная проекция прямойобладает собирательным свойством: проекции всех точек прямой расположены в одной точке чертежа.

Прямые уровня и проецирующие прямые называются прямыми частного положения.

Рассмотрев различные положения прямой относительно плоскостей проекций можно сформулировать следующее правило:

Если на ортогональном чертеже (эпюре) одна из двух заданных проекций прямой параллельна координатной оси или вырождается в точку, то на другой проекции прямая отобразилась в натуральную величину.

Источник

Взаимное расположение прямой и плоскости

Занятие 2

Прямая и плоскость в ортогональных проекциях

Необходимые определения:

Если плоскость параллельна или перпендикулярна одной из плоскостей проекций она является плоскостью частного положения – уровенной или проецирующей соответственно.

Свойство проецирующей плоскости – проекции всех геометрических элементов, лежащих в проецирующей плоскости, лежат на вырожденной проекции плоскости, совпадающей со следом плоскости.

Для построения линии пересечения двух плоскостей необходимо найти две их общие точки и соединить их.

Если одна из плоскостей является плоскостью частного положения, то с вырожденной проекцией плоскости совпадает одна проекция линии пересечения. Другая проекция линии пересечения выстраивается по принадлежности другой плоскости.

Конкурирующие точки – точки, лежащие на одном проецирующем луче. Из пары конкурирующих точек видима та, у которой больше координата, определяющая расстояние до заданной плоскости проекций.

Задача 4: Построить линию пересечения двух плоскостей. Определить видимость плоскостей относительно друг друга. Отмыть видимые участки плоскостей.

На рисунке 33.а представлена плоскость четырехугольника ABCD, которая является плоскостью общего положения. Если плоскость задается плоской фигурой в виде четырехугольника, то этот четырехугольник должен базироваться на двух параллельных прямых, т.е. быть параллелограммом, трапецией или прямоугольником.

Если задана плоскость общего положения, то обе заданные проекции должны быть в виде многоугольников одинаковой формы. Если задан выпуклый многоугольник, то обе проекции плоскости должны быть выпуклыми многоугольниками.

Вторая плоскость MNKE, задана прямоугольником, является плоскостью частного положения.

Признаком плоскости частного положения является наличие вырожденной проекции плоскости.

Вырожденной проекцией геометрического элемента называется проекция, не соответствующая форме элемента в пространстве. Вырожденной проекцией прямой является точка, вырожденной проекцией плоскости – прямая.

Плоскость MNKE является горизонтальной плоскостью (рис.33.б ), т.к. фронтальная проекция заданной плоскости представляет собой прямую, параллельную оси х.

Для построения линии пересечения двух плоскостей необходимо найти две их общие точки и соединить их.

Построение линии пересечения двух плоскостей, одна из которых частного положения, базируется на следующем правиле:

Если одна из плоскостей является плоскостью частного положения, то одна проекция линии пересечения задана и совпадает со следом этой плоскости. Вторая проекция линии пересечения достраивается с учетом принадлежности другой плоскости.

В нашем примере на рисунке 34 фронтальная проекция плоскости MNKE совпадает с фронтальным следом этой плоскости, поэтому у нас задана фронтальная проекция линии пересечения двух плоскостей, которая лежит на следе этой плоскости.

Горизонтальную проекцию линии пересечения m₁ достраиваем с учетом принадлежности плоскости параллелограмма ABCD с помощью точек 1 и 2, лежащих на сторонах ABиCD соответственно.

Любая задача на построение пересечения геометрических элементов заканчивается определением видимости этих элементов относительно друг друга.

Видимость проще всего определяется с помощью конкурирующих точек.

Из пары конкурирующих точек видима та, у которой больше координата, определяющая расстояние до заданной плоскости проекций.

Видимость плоскостей относительно друг друга необходимо определить на горизонтальной плоскости проекций, до которой определяет расстояние координата z.

На чертеже рисунка 35 конкурирующими точками являются точки 3 и 4, лежащие на сторонах KEиBC соответственно. Горизонтальные проекции этих точек совпадают между собой (3₁≡ 4₁), а фронтальные – лежат на фронтальных проекциях прямых KEиBC. Координата z точки 4 больше координаты z точки 3, поэтому 4₁ расположена над 3₁, а следовательно, видима прямая ВС.

3₁≡ 4₁; 3Î KE, 4Î ВС;

z₄ > z₃ Þ точка 4 находится над точкой 3

Þ прямая ВС находится над прямой KE

Þ прямая ВС Dвидима, прямая KE– не видима

Þ плоскость ABCD – видима, плоскость MNKE – не видима.

Если в одну сторону от линии пересечения видима одна плоскость (ABCD), то в другую сторону видима другая плоскость (MNKE).

Видимые стороны плоскостей обводятся основной сплошной толстой линией, невидимые стороны – штриховой.

Решение домашней работы № 4.

На рисунке 36 представлен итоговый чертеж решения домашней задачи №4. Видимые участки двух плоскостей выделяются цветом в технике «отмывка». Видимые стороны плоскостей обводятся основной сплошной толстой линией, невидимые стороны – штриховой. Сохраняются все линии построения, выполняемые сплошными тонкими линиями, и надписи.

Взаимное расположение прямой и плоскости

Источник

Ортогональное проецирование прямой линии

4.1. Общие понятия и определения. Прямая в пространстве и на ортогональном чертеже может быть задана: а) двумя точками; б) точкой и направлением прямой; в) двумя пересекающимися плоскостями.

Определение. На эпюре точка лежит на прямой, если её проекции расположены на одноимённых проекциях этой прямой (рис. 5).

4.2. Расположение прямой относительно плоскостей проекций

В рассматриваемом разделе производится оценка проекционных свойств прямых в зависимости от их расположения относительно плоскостей проекции П₁, П₂ и П₃. При этом прямые в основном задаются лишь двумя своими проекциями (горизонтальной и фронтальной).

Прямая общего положения – это прямая, не перпендикулярная ни одной из плоскостей проекций (П₁, П₂ или П₃). Эпюрный опознавательный признак (ЭОП) прямых общего положения – обе заданные проекции прямых непараллельны и неперпендикулярны к координатным осям (рис. 6).

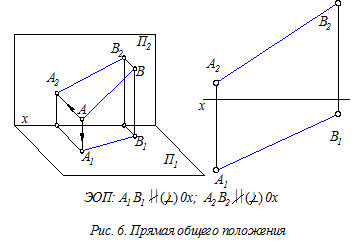
Проекционные свойства (ПС) прямых общего положения – длина прямых и углы их наклона к плоскостям проекций на ортогональном чертеже искажены, т. е. показаны не в натуральную величину.

ЭОП прямых уровня: одна из заданных проекций прямой уровня параллельна координатной оси (0х или 0 z). Это означает, что одна из трёх координат любой точки прямой уровня постоянна (т.е. не изменяется).

Определение. Вырожденной проекцией прямой называется точка ортогонального чертежа, где отобразились все точки этой прямой.

Вырожденная проекция прямойобладает собирательным свойством: проекции всех точек прямой расположены в одной точке чертежа.

Прямые уровня и проецирующие прямые называются прямыми частного положения.

Рассмотрев различные положения прямой относительно плоскостей проекций можно сформулировать следующее правило:

Если на ортогональном чертеже (эпюре) одна из двух заданных проекций прямой параллельна координатной оси или вырождается в точку, то на другой проекции прямая отобразилась в натуральную величину.

4.3. Определение натуральной величины отрезка прямой общего положения и углов наклона этой прямой к плоскостям проекций

На эпюре задан отрезок АВ (А₁В₁, А₂В₂) прямой общего положения (рис. 13). Требуется графически определить его длину и углы наклона к плоскостям проекций П₁ и П₂.

Источник

Глава 8. Поверхности

§ 47. Расположение плоскости относительно плоскостей проекций. Взаимное расположение двух плоскостей

К плоскостям общего положения относятся плоскости, не параллельные и не перпендикулярные ни одной из плоскостей проекций. На комплексном чертеже (см. рис. 88) проекции элементов, которыми задана плоскость, как правило, занимают общее положение.

К плоскостям частного положения относятся плоскости, параллельные или перпендикулярные одной из плоскостей проекций.

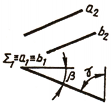
В свою очередь, плоскости частного положения делятся на проецирующие плоскости и плоскости уровня. К проецирующим плоскостям относятся плоскости, перпендикулярные к одной из плоскостей проекций. Все проецирующие плоскости будем обозначать Σ. Проецирующие плоскости могут быть перпендикулярны к П₁, П₂ или П₃. В зависимости от этого различают горизонтально проецирующие плоскости, когда Σ ⊥ П₁; фронтально проецирующие плоскости, когда Σ ⊥ П₂; профильно проецирующие плоскости, когда Σ ⊥ П₃.

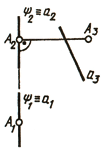
Проецирующая плоскость отличается тем, что проекция ее на плоскость проекций, ей перпендикулярную, всегда изображается в виде прямой линии. На этой линии располагаются проекции всех точек, линий и фигур, лежащих в проецирующей плоскости. Проекция плоскости, вырожденной в прямую, вполне определяет положение плоскости относительно плоскостей проекций. Например, приведен комплексный чертеж плоскости Σ, заданной двумя параллельными прямыми (рис. 89, а).

Отсюда видно, что Σ(a ׀׀ b) является горизонтально проецирующей плоскостью и расположена под углом β к фронтальной плоскости проекций и под углом γ к профильной плоскости проекций.

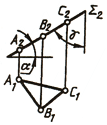
На рис. 89, б приведен комплексный чертеж плоскости Σ, составляющей угол а с горизонтальной плоскостью проекций и угол у с фронтальной плоскостью проекций. Это можно записать так: ∆АВС ∈ А₂ ∈ Σ₂, В₂ ∈ Σ₂, C₂ ∈ Σ₂.

Наличие вырожденной проекции дает возможность задавать проецирующие плоскости на комплексном чертеже только одной проекцией. На рис. 89, в через точку А проведена профильно проецирующая плоскость (Σ ⊥ П₃) под углом α к П₃.

Все изображения, расположенные в заданной плоскости, на плоскости, не перпендикулярные к ней, проецируются с искажением.

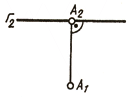
На рис. 90, а дан комплексный чертеж плоскости горизонтального уровня (Г ׀׀ П₁);

на рис. 90, в показан комплексный чертеж профильно проецирующей плоскости (Ψ ׀׀ П₃, ΨаА; А ∈ а).

Плоскости уровня отличаются тем, что на плоскости проекций, им перпендикулярную, они проецируются в прямую линию, на которой располагаются точки, прямые и фигуры, расположенные в плоскости уровня. Эти прямые являются вырожденными проекциями заданной плоскости. На плоскость проекций, параллельную заданной плоскости, все изображения этой плоскости проецируются без искажений, т. е. в натуральную величину.

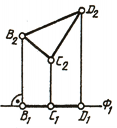
Две плоскости в пространстве могут быть параллельными или пересекаться. Параллельными будут плоскости, если одна из них задана пересекающимися прямыми, параллельными пересекающимся, задающим вторую плоскость; на рис. 91 показаны параллельные плоскости: Σ₁(ab) и Σ₂(cd), причем а ׀׀ с, а b ׀׀ d.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Источник

Способ дополнительного проецирования

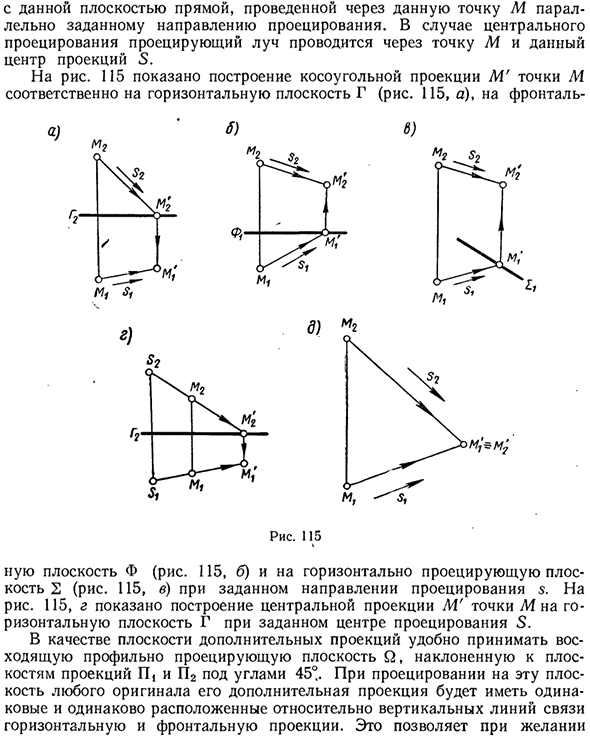
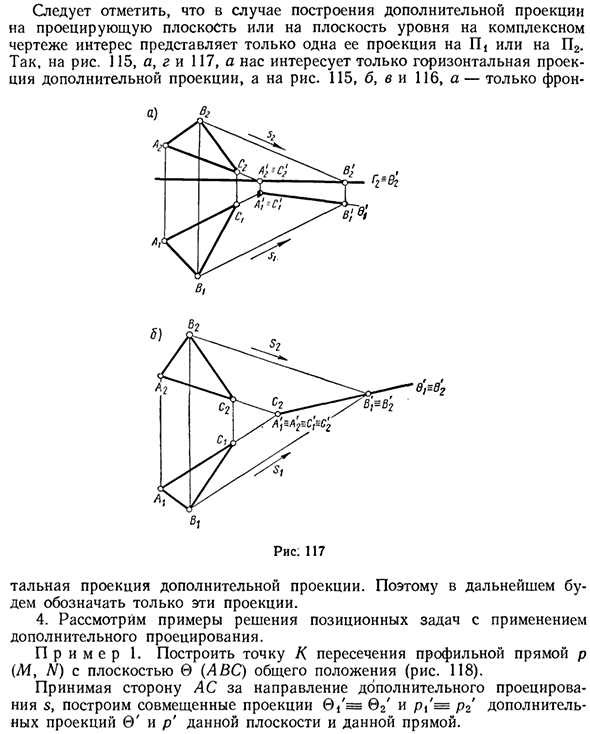
Способ дополнительного проецирования

Обычно используется наклонная или центральная проекция на горизонтальной или проекционной поверхности. Людмила Фирмаль

Целью использования дополнительных проекций является получение той или иной исходной вырожденной проекции при решении задачи о местоположении. Как известно, решение проблем с местоположением значительно упрощено. Поскольку решение является более сложным, чем использование базового метода преобразования сложных чертежей, нецелесообразно использовать дополнительные проекции для решения метрических задач. 2.

Наклонная проекция M ‘точки M на заданную плоскость для заданного направления s проекции является пересечением. Он имеет заданную плоскость с линией, проходящей через заданную точку M, параллельной заданному направлению проекции. В случае центральной проекции проекционный луч проходит через точку M и центр S этой проекции.

В качестве дополнительной плоскости проекции удобно иметь восходящий профиль, который проецирует плоскость Q, наклоненную относительно плоскостей проекции P и P2, под углом 45 °. При проецировании на эту исходную плоскость дополнительные проекции в равной степени располагаются в одном и том же положении относительно горизонтальной линии и вертикальной линии фронтальной проекции.

Это позволяет вам г) м2 Рис. 115 В сложных чертежах объедините горизонтальную проекцию и фронтальную проекцию оригинальной дополнительной проекции. Это обеспечивает известное упрощение в некоторых случаях. На фиг.115e показана конфигурация комбинированной проекции косой проекции M ‘точки M на плоскость Q для заданного направления s проекции.

Легко понять ранее использовавшуюся прямую рефракцию прерывистой линии при решении задач положения с использованием прямых профилей Рисунок 116 Связи можно интерпретировать как комбинированные проекции дополнительных проекций данных линии профиля на плоскость Q. 3. Теперь рассмотрим конструкцию дополнительной косой проекции линий и плоскостей.

В этом случае вы устанавливаете цель для такой структуры и получаете вырожденную проекцию линий и плоскостей. То есть прямая проецируется на точку, а плоскость проецируется на прямую. Предположим, нам нужно создать вырожденную проекцию данной линии a на фронтальную плоскость (рис. 116, а).

Для этого выберите направление проекции s, параллельное линии a, и представьте проекцию линии a точкой a ‘. На рисунках 116 и b показана конфигурация комбинированной проекции. Вырожденная линия проекции а. Чтобы создать вырожденную проекцию плоскости, достаточно выбрать направление проекции s, параллельное указанной плоскости.

На фиг.117а показана конфигурация проекции плоскости 0 (LAN) на горизонтальную плоскость Γ, а на фиг.11 направление s C> 40 проекции на фиг.1. Сделано Дополнительная проекция этой плоскости — прямая. При создании дополнительных проекций на плоскости проекции сложного чертежа или горизонтальной плоскости учитывается только одна проекция на P или P2.

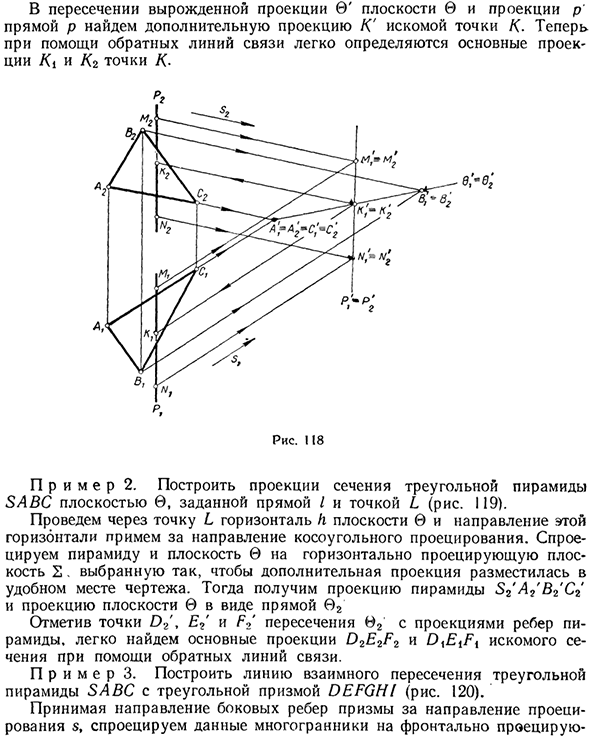
Пример 1. Постройте пересечение K между линией профиля p (M, N) и плоскостью общего положения (ABC) (рис. 118). Постройте эту плоскость с дополнительными выступами 6 / = © 2 ‘и дополнительными выступами pg 0’ и p ‘, используя сторону AC направления дополнительных выступов.

В а) в Найти дополнительную проекцию K ‘для искомой точки K на пересечении вырожденной проекции 0’ на плоскости 0 и проекции p на прямой p. Людмила Фирмаль

Здесь основные выступы Ki и K2 могут быть легко определены с использованием обратной линии связи. Точка К • ERE; Пример 2. Создайте проекцию сечения треугольной пирамиды SABC, заданной линией I и точкой L (рисунок 119). Нарисуйте горизонтальную плоскость 0 плоскости 0, проходящую через точку L, и это горизонтальное направление является направлением наклонной проекции.

Проецирует пирамиду и плоскость 0 на плоскость 2, которая выступает горизонтально. Выберите для размещения дополнительных выступов в удобных местах на чертеже. Далее получаем проекцию пирамиды S2A2B2’C2 и проекцию плоскости 0 в виде линии 02. D2 \ £, чтобы отметить точку?

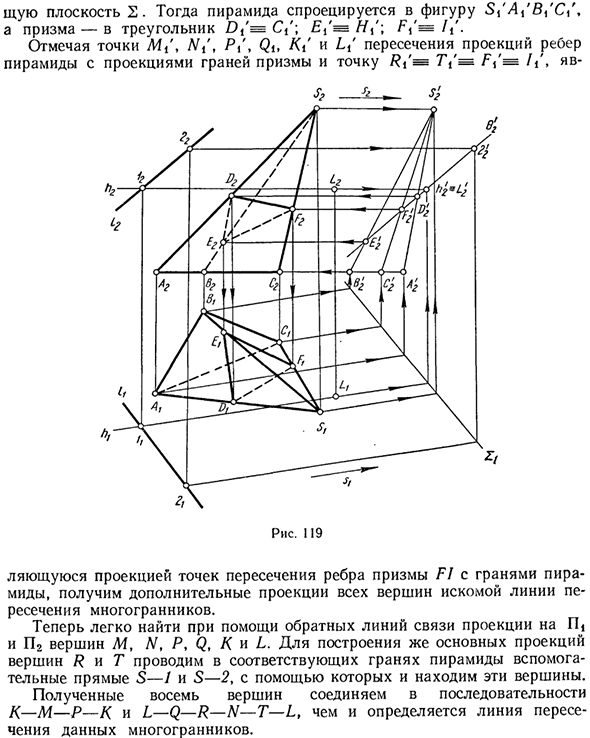
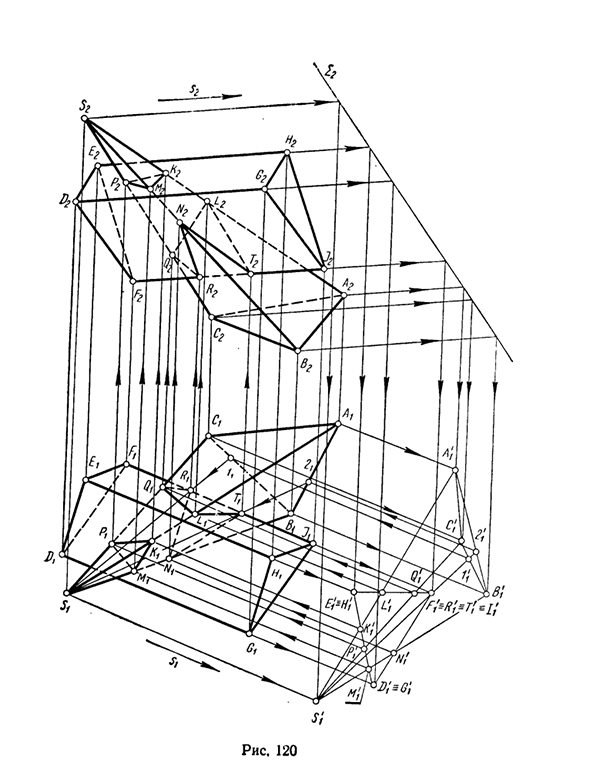
‘И / Н2 и пересечение V проекции края пирамиды, используя обратную линию связи, вы можете легко найти основные проекции D2E2F2 и DxEiFt в нужном сечении. Пример 3. Нарисуйте линию пересечения между треугольной пирамидой SABC и треугольной призмой DEFGHI (Рисунок 120).

Проецирует эти многогранники на переднюю проекцию с направлением бокового края призмы в качестве направления проекции s. Рисунок 118 Самолет 2. Далее пирамида проецируется на фигуру S \ AX’BX’C \, а призма проецируется на треугольник D / = C /. £, ‘= //,’; / Vs /, ‘. Отметьте точку M /, DO /. I /, Qi, / C / и Lt ‘пересечение проекции края пирамиды и грани призмы и точки Ri =’ 7Y = F% = /, ‘ S? 4-х>

Используйте проекцию пересечения края призмы FI и грани пирамиды, чтобы получить дополнительную проекцию всех вершин искомой линии пересечения многогранника. Теперь вы можете легко найти проекции вершин М, N, Р, Q, К, L П и П2, используя обратную линию связи.

Создать основные проекции вершин R и Т с помощью нахождения 5 этих вершин на соответствующих гранях пирамиды. Получающиеся восемь вершин связаны последовательностями K-M-P-K и L-Q-R-N-T-L, которые определяют линии пересечения этих многогранников.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник