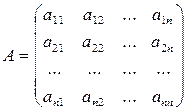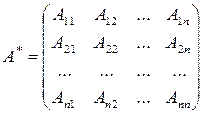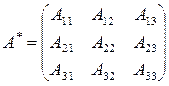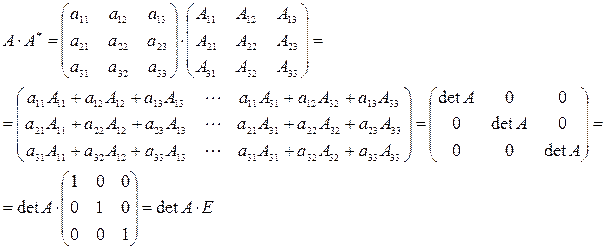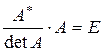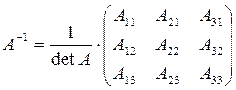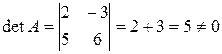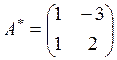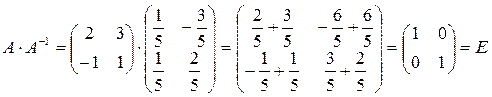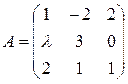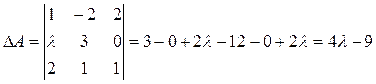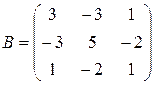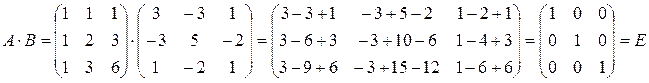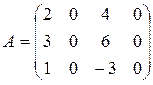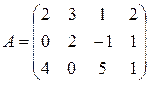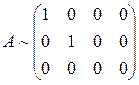Что такое вырожденная и невырожденная матрица
Определение ранга матрицы. Вырожденные и невырожденные матрицы. Матричная запись системы линейных уравнений
Определение матрицы. Понятие подматрицы. Операции над матрицами и их свойства.
Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. Числа составляющие матрицу называются элементами матрицы. Подматрицей матрицы А является матрица, которая состоит из невычеркнутых элементов первоначальной матрицы.
Операции над матрицами:
· Сложение матриц. Они должны быть одинаковой размерности и одноимённые элементы складываются.
· Умножение матриц на число.
· Вычитание матриц. А-В=А=(-1)В
· Умножение матриц. Правило умножения: Произведением матриц АВ называется такая матрица С каждый элемент которой равен сумме произведений элементов итой строки матрицы А на элементы житого столбца матрицы В.
Деления в матрицах нет!
· А Т *(В+С)= А Т *В+ А Т *С
· А*Е(единичная матрица)=А или Е*А=А
· А*(В*С)=(А*В)*С главное порядок
Понятие определителя квадратной матрицы порядка n. Свойства определителей. Методы вычисления определителей. Примеры.
Определитель – число, характеризующее квадратную матрицу.
Вырожденная матрица – определитель = 0
Невырожденная матрица – определитель ≠ 0
Определитель матрицы первого порядка = элементу этой матрицы.
Определитель матрицы второго порядка, называется число которое вычисляется по формуле:
Определитель матрицы третьего порядка, называется число которое вычисляется по формуле (правило треугольника или правило Саррюса):
Определители n-го порядка
Теорема: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраическое дополнение.
Это метод вычисления определителей, и его называют метод разложения по элементам какой-либо строки или какого-либо столбца.
Определитель диагональной матрицы = произведению элементов главной диагонали.
· Если какая-нибудь строка (столбец) состоит только из нулей, то её определитель равен нулю.
· Если все элементы какой-либо строки (столбца) умножить на число, то и весь определитель умножается на число.
· При транспонировании матрицы её определитель не изменится.
· При перестановке двух строк или столбцов матрицы, её определитель меняет знак на противоположный.
· Если квадратная матрица содержит две одинаковые строки или столбца, то её определитель будет равен нулю.
· Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель будет равен нулю.
· Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраическое дополнение элементов другой строки или столбца этой матрицы равна нулю.
· Определитель матрицы не изменится если к элементам какой-либо строки или столбца матрицы прибавить элементы другой строки (столбца) предварительно умноженное на одно и тоже число. Получаем нули.
· Определитель произведения двух матриц равен произведению двух определителей.
Определение обратной матрицы. Теорема о необходимом и достаточном условии существования обратной матрицы. Вычисление обратной матрицы (на примере).
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Алгоритм вычисления обратной матрицы:
Определение ранга матрицы. Вырожденные и невырожденные матрицы. Матричная запись системы линейных уравнений.
Рангматрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Вырожденная матрица – определитель = 0
Невырожденная матрица – определитель ≠ 0
Матричная запись системы линейных уравнений:
Невырожденная матрица
Невырожденная матрица (иначе Неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае она называется вырожденной.
Для квадратной матрицы 
Полезное
Смотреть что такое «Невырожденная матрица» в других словарях:
невырожденная матрица — неособенная матрица — [http://www.iks media.ru/glossary/index.html?glossid=2400324] невырожденная матрица Квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов).… … Справочник технического переводчика
Невырожденная матрица — [non singular matrix] квадратная матрица, определитель которой отличен от нуля; ее столбцы линейно независимы (см. Линейная зависимость векторов). Квадратная матрица обратима тогда и только тогда, когда она невырожденная … Экономико-математический словарь
невырожденная матрица — neypatingoji matrica statusas T sritis fizika atitikmenys: angl. non singular matrix; regular matrix vok. nichtausgeartete Matrix, f; nichtsinguläre Matrix, f; reguläre Matrix, f rus. невырожденная матрица, f; неособенная матрица, f pranc.… … Fizikos terminų žodynas
НЕВЫРОЖДЕННАЯ МАТРИЦА — неособенная матриц а, квадратная матрица, определитель к рой отличен от нуля. Для квадратной матрицы Анад полем невырожденность эквивалентна каждому из следующих условий: 1)A обратима; 2) строки (столбцы) матрицы Алинейно независимы; 3)… … Математическая энциклопедия
МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Обратная матрица — Обратная матрица такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для… … Википедия
ЖОРДАНОВА МАТРИЦА — квадратная блочно диагональная матрица J над полем к, имеющая вид где Jm(l) квадратная матрица порядка твида Матрица J т(l)называется жордановой клеткой порядка m с собственным числом к. Каждая клетка определяется элементарным делителем (см. [5]) … Математическая энциклопедия
Вырожденная матрица — Вырожденной или сингулярной называют квадратную матрицу, определитель которой равен нулю. Эквивалентные условия вырожденности Используя различные понятия линейной алгебры, можно привести различные условия вырожденности: Строки или столбцы матрицы … Википедия
Вырожденная матрица
Вы́рожденной или сингуля́рной называют квадратную матрицу, определитель которой равен нулю.
Эквивалентные условия вырожденности
Используя различные понятия линейной алгебры, можно привести различные условия вырожденности:
Свойства
См. также
Полезное
Смотреть что такое «Вырожденная матрица» в других словарях:
вырожденная матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] вырожденная матрица Квадратная матрица, определитель которой равен нулю. Для экономических расчетов (например, в области межотраслевых балансов) важно, что В.м. не может иметь… … Справочник технического переводчика
Вырожденная матрица — [degenerate matrix] квадратная матрица, определитель которой равен нулю. Для экономических расчетов (например, в области межотраслевых балансов) важно, что В.м. не может иметь обратной, т.е. с ней нельзя произвести операцию обращения матрицы … Экономико-математический словарь
вырожденная матрица — ypatingoji matrica statusas T sritis fizika atitikmenys: angl. singular matrix vok. ausgeartete Matrix, f; singuläre Matrix, f rus. вырожденная матрица, f; особенная матрица, f pranc. matrice singulière, f … Fizikos terminų žodynas
ВЫРОЖДЕННАЯ МАТРИЦА — особая матрица, сингулярная матрица, квадратная матрица, определитель к рой равен нулю … Математическая энциклопедия
Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь
матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика
МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
особенная матрица — ypatingoji matrica statusas T sritis fizika atitikmenys: angl. singular matrix vok. ausgeartete Matrix, f; singuläre Matrix, f rus. вырожденная матрица, f; особенная матрица, f pranc. matrice singulière, f … Fizikos terminų žodynas
ЧАСТЬ 2. НЕВЫРОЖДЕННЫЕ МАТРИЦЫ
Дата добавления: 2015-08-14 ; просмотров: 6115 ; Нарушение авторских прав
3.1. Основные понятия
Пусть А — квадратная матрица n-го порядка
Квадратная матрица А называется невырожденной, если определитель Δ = det А не равен нулю: Δ = det А ≠ 0. В противном случае (Δ = 0) матрица А называется вырожденной.
Матрицей, союзной к матрице А, называется матрица
где Aij — алгебраическое дополнение элемента аij данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
3.2. Обратная матрица
Теорема 3.1.Всякая невырожденная матрица имеет обратную.
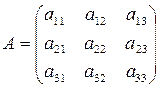
Составим союзную матрицу
и найдем произведение матриц А и А *
Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2). Аналогично убеждаемся, что
Равенства (3.2) и (3.3) перепишем в виде
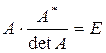
Сравнивая полученные результаты с определением (3.1), получаем
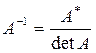
Отметим свойства обратной матрицы:
1. 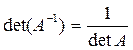
Решение: 1) Находим det A:
Решение: Всякая невырожденная матрица имеет обратную. Найдем определитель матрицы А:
Пример 3.3. Показать, что матрица А является обратной для В, если
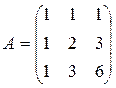
Решение: Найдем произведение матриц А и В:
Аналогично В · А = Е. Следовательно, матрица А является обратной для В.
Рассмотрим матрицу А размера, т х п.
Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделен минор 2-го порядка. (Заметим, что таких миноров можно составить 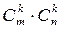
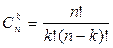
Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(А) или rang A.
Очевидно, что 0 ≤ г ≤ min(m; n), где min(m; n) — меньшее из чисел m и п.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
Пример 3.4. Найти ранг матрицы:
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 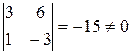
Отметим свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы (см. с. 12).
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример 3.5. Найти ранг матрицы используя результаты примера 1.4.
Решение: В примере 1.4 показано, что
Таким образом, ранг матрицы А равен r(А) = 2.
Вырожденная матрица
Вы́рожденной или сингуля́рной называют квадратную матрицу, определитель которой равен нулю.
Эквивалентные условия вырожденности
Используя различные понятия линейной алгебры, можно привести различные условия вырожденности:
Свойства
См. также
Полезное
Смотреть что такое «Вырожденная матрица» в других словарях:
вырожденная матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] вырожденная матрица Квадратная матрица, определитель которой равен нулю. Для экономических расчетов (например, в области межотраслевых балансов) важно, что В.м. не может иметь… … Справочник технического переводчика
Вырожденная матрица — [degenerate matrix] квадратная матрица, определитель которой равен нулю. Для экономических расчетов (например, в области межотраслевых балансов) важно, что В.м. не может иметь обратной, т.е. с ней нельзя произвести операцию обращения матрицы … Экономико-математический словарь
вырожденная матрица — ypatingoji matrica statusas T sritis fizika atitikmenys: angl. singular matrix vok. ausgeartete Matrix, f; singuläre Matrix, f rus. вырожденная матрица, f; особенная матрица, f pranc. matrice singulière, f … Fizikos terminų žodynas
ВЫРОЖДЕННАЯ МАТРИЦА — особая матрица, сингулярная матрица, квадратная матрица, определитель к рой равен нулю … Математическая энциклопедия
Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь
матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика
МАТРИЦА — прямоугольная таблица состоящая из т строк и n столбцов; её паз. M. размера Элементами(первый индекс указывает номер строки, второй номер столбца) M. могут быть числа, ф ции пли др. величины, над к рыми можно производить алгебраич. операции. M.… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
особенная матрица — ypatingoji matrica statusas T sritis fizika atitikmenys: angl. singular matrix vok. ausgeartete Matrix, f; singuläre Matrix, f rus. вырожденная матрица, f; особенная матрица, f pranc. matrice singulière, f … Fizikos terminų žodynas