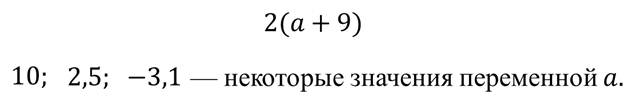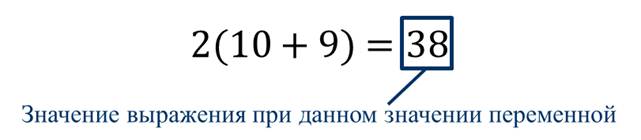Что такое выражение с переменными 7 класс определение
Числовые, буквенные выражения и выражения с переменными: определения, примеры.
Запись условий задач с помощью принятых в математике обозначений приводит к появлению так называемых математических выражений, которые называют просто выражениями. В этой статье мы подробно поговорим про числовые, буквенные выражения и выражения с переменными: дадим определения и приведем примеры выражений каждого вида.
Навигация по странице.
Числовые выражения – что это?
Можно сделать вывод, что на этом этапе изучения математики числовыми выражениями называют имеющие математический смысл записи, составленные из чисел, скобок и знаков сложения и вычитания.
А в старших классах разнообразие записей числовых выражений разрастается как снежный ком, катящийся с горы. В них появляются обыкновенные и десятичные дроби, смешанные числа и отрицательные числа, степени, корни, логарифмы, синусы, косинусы и так далее.
Обобщим всю информацию в определение числового выражения:
Разъясним все составные части озвученного определения.
В числовых выражениях могут участвовать абсолютно любые числа: от натуральных до действительных, и даже комплексных. То есть, в числовых выражениях можно встретить
Что касается скобок, то имеют место как числовые выражения, в которых есть скобки, так и выражения без них. Если в числовом выражении есть скобки, то они в основном
В качестве специальных математических символов и обозначений, которые можно встретить в числовых выражениях, приведем знак модуля. Для примера покажем числовое выражение с модулем 
Что такое буквенные выражения?
Итак, если допустить в числовом выражении присутствие букв, которыми обозначены некоторые числа, то получится так называемое буквенное выражение. Дадим соответствующее определение.
Выражение, содержащее буквы, которыми обозначены некоторые числа, называется буквенным выражением.
Из данного определения понятно, что принципиально буквенное выражение отличается от числового выражения тем, что может содержать буквы. Обычно в буквенных выражениях используются маленькие буквы латинского алфавита ( a, b, c, … ), а при обозначении углов – маленькие буквы греческого алфавита ( α, β, γ, … ).
Итак, буквенные выражения могут быть составлены из чисел, букв и содержать все математические символы, которые могут встречаться в числовых выражениях, такие как скобки, знаки корней, логарифмы, тригонометрические и другие функции и т.п. Отдельно подчеркнем, что буквенное выражение содержит по крайней мере одну букву. Но может содержать и несколько одинаковых или различных букв.
Выражения с переменными
Если в буквенном выражении буква обозначает величину, которая принимает не какое-то одно конкретное значение, а может принимать различные значения, то эту букву называют переменной и выражение называют выражением с переменной.
Выражение с переменными – это буквенное выражение, в котором буквы (все или некоторые) обозначают величины, принимающие различные значения.
Вообще, переход от понятия буквенного выражения к выражению с переменными происходит в 7 классе, когда начинают изучать алгебру. До этого момента буквенные выражения моделировали какие-то конкретные задачи. В алгебре же начинают смотреть на выражение более общо, без привязки к конкретной задаче, с пониманием того, что данное выражение подходит под огромное число задач.
В заключение этого пункта обратим внимание еще на один момент: по внешнему виду буквенного выражения невозможно узнать, являются ли входящие в него буквы переменными или нет. Поэтому ничто нам не мешает считать эти буквы переменными. При этом разница между терминами «буквенное выражение» и «выражение с переменными» исчезает.
2. Выражения с переменными
Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за 3 ч — 60 • 3 км, за 5 ч — 60-5 км, за 5,5 ч — 60 • 5,5 км. Вообще за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t — виражением с переменной.
Если в выражение с переменными подставить вместо каждой переменной какое-либо её значение, то получится числовое выражение. Его значение называют значением вы ражения с переменными при выбранных значениях переменных.
Так, число 88 есть значение выражения ab при a = 8 и b = 11, число 100 есть значение этого выражения при а = 25 и b = 4.
Рассмотрим выражение 

Некоторые выражения имеют смысл нри всех значениях переменных. Примерами могут служить выражения
Выражения с переменными используются для записи формул.
Любое чётное число m можно представить в виде произведения числа 2 и целого числа n, т. е.
Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут чётные числа. Формулу m = 2n называют формулой чётного числа.
Формулу m = 2n + 1, где n — целое число, называют формулой нечётного числа.
Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу.
Например, формулу числа, кратного 3, можно записать так: m = Зn, где n — целое число.
а) кратного 5; б) кратного 10; в) кратного 101.
а) 3% этого числа равны 1,8;
б) 85% этого числа равны 17;
в) 130% этого числа равны 3,9;
Выражения с переменными
Урок 2. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Выражения с переменными»
· ввести понятие «выражение с переменными»;
· ввести понятие «область определения выражения».
Вспомним, что на прошлом уроке мы говорили о числовых выражениях и значениях числовых выражений.
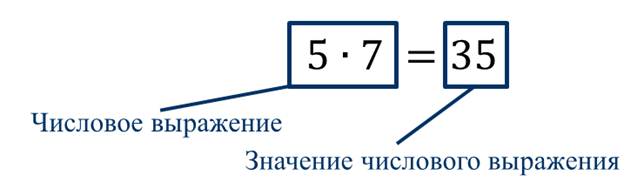
Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.
Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.
Буквенным выражением называется запись, состоящая из чисел, букв, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.
Строчные буквы латинского алфавита чаще всего используют при записи буквенных выражений.
Следует также знать, что и одна буква является буквенным выражением.
Давайте решим задачу.
Велосипедист двигается со скорость 15 километров в час. Какой путь он проедет за время t?
Известно, что путь можно найти скорость умножив на время. Тогда путь, который проедет велосипедист, будет равен 15t.
Теперь, если нам нужно будет узнать, какое расстояние проехал велосипедист, например, за 3 часа, мы подставим в выражение 15 ∙ t вместо буквы t число 3, то есть найдём значение выражения при t = 3, и получим 45 километров.
В нашем случае буква t называется переменой, а само выражение – выражением с переменной.
То есть, переменная – это буква, входящая в буквенное выражение, которая может принимать различные значения.
Если мы в выражение с переменной вместо переменной подставим число, то получим числовое выражение.
Теперь, прежде, чем перейти к решению упражнений, вернёмся к выражению 15t, которое мы получили при решении первой задачи. Здесь переменная t может принимать только положительные значения, так как время не может быть отрицательным, и это множество значений называется областью определения выражения 15t.
Таким образом, важно помнить, что в область определения любого выражения могут входить только те значения переменных, при которых получается числовое равенство, имеющее смысл.
А сейчас давайте решим некоторые упражнения.
Понятие и виды алгебраических выражений
п.1. Математические символы и выражения
В математическом языке мы используем особенные «слова», которые называются математическими выражениями, при этом «буквами» нам служат математические символы.
Список математических символов постоянно пополняется. Ведь при написании своей работы каждый вправе изобрести собственный иероглиф-символ, объяснить его смысл с помощью определения и предложить правила применения. Если символ окажется удачным и востребованным, то со временем он появится в других работах и начнёт самостоятельный путь по миру.
Допустим, по правилам, мы строим математические выражения, которые состоят из различных чисел (образованных цифрами, дробной чертой и десятичной запятой), знаков арифметических операций, возведения в рациональную степень, корней и скобок:
п.2. Определение и понятие переменной
Математические выражения с переменными также могут быть термами или формулами.
Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (или возведения переменных в степень с дробным показателем), то его называют целым выражением.
Примеры целых выражений:
Если алгебраическое выражение, кроме признаков целого выражения, содержит также деление на переменные, то его называют дробным выражением.
Примеры дробных выражений:
Целые и дробные выражения объединяют в класс рациональных выражений.
Если алгебраическое выражение содержит извлечение корня из переменных (или возведение переменных в степень с дробным показателем), то его называют иррациональным выражением.
Примеры иррациональных выражений:
п.4. Примеры
Значения выражений слева и справа действительно равны, формула истинна.
Ответ: формула истинна
Подставляем значения переменных:
Пример 4. Для проведения экзамена закупили k пачек бумаги по p рублей и m картриджей для принтера по q рублей. Напишите формулу, по которой можно найти общую сумму расходов S.
Значения выражений слева и справа действительно равны, формула истинна.
Тема. Выражения с переменными.
Тема . Выражения с переменными.
I. Организационный момент.
II. Проверка домашнего задания.
III. Актуализация опорных знаний.
1. Теоретический опрос фронтально.
1. Что называется числовым выражением?
2. Для чего в записи числового выражения присутствуют скобки?
3. Когда числовое выражение имеет смысл? Приведите пример такого выражения.
4. Когда числовое выражение не имеет смысла? Приведите пример такого выражения.
5. Что называется значением числового выражения?
6. Каков порядок выполнения действий при нахождении значения числового выражения?
1. Назовите числовые выражения, не имеющие смысла:
а) 


г) 


2. Найдите значение числового выражения.
а) 



д) 



IV. Объяснение нового материала.
Выражения с переменными.
1. Мотивация изучения.
При решении многих практических задач удобно для обозначения различных чисел использовать буквы.
Например, если a и b – длины сторон прямоугольника, то выражение a ∙ b показывает способ вычисления его площади и т.д.
Если в числовом выражении некоторые (или все) входящие в него числа заменить буквами, то получим выражение с переменными (переменной).
Пример 1. 






3. Нахождение значения выражения с переменной.
1) Подставить вместо переменных их значения;
2) Найти числовое значение.
2х + 3у, если х = 

1) 



4. Допустимые значения переменных.
Пример 3. Найдите допустимые значения переменной:
1) 3х – 27. Ответ: х – любое число.
2) 
7х – 14 ≠ 0, х ≠ 2. Ответ: х – любое число, кроме 2.
3) 

V. Формирование умений и навыков.
1. Найдите значение выражения х + 3,2 при х = – 6,8; – 3,2; 
1) если х = – 6,8, то – 6,8 + 3,2 = – 3,6;
3) если х = 

Уч.с.10 № 24(б). Вычислите значение выражения 
б) если х = – 3,6, у = 5, то 
Уч.с.10 № 26(б). Известно, что при некоторых значениях х и у значение выражения х – у равно 0,7. Какое значение принимает при тех же х и у выражение: б) у – х.
б) если х – у = 0,7, то у – х = – (х – у) = – 0,7.
Уч.с.10 № 29. Опытное поле разбили на два участка. Площадь первого участка а га, а второго b га. С каждого гектара первого участка собрали 32 ц пшеницы, а с каждого гектара второго участка собрали 40 ц пшеницы. Сколько пшеницы собрали с обоих участков? Вычислите при а = 120, b = 80.

S 2 = b га, собрали по 40 ц с каждого га
32 ∙ 120 + 40 ∙ 80 = 3840 + 3200 = 7040 (ц). Ответ: 7040 ц.
VI. Подведение итогов урока.
1. Что называется выражением с переменной?
2. Может ли выражение состоять из одной буквы? А числа?
3. Как найти значение выражения с переменной при определенном значении переменной?
4. Какие способы записи можно использовать при нахождении значения выражения с переменной?
VII. Домашнее задание. п. 2 (выучить теорию). № 20, 24(а,в), 26(а,в), 30.