Что такое выпуклый угольник
Какой многоугольник называется выпуклым
Что такое выпуклый многогольник
Выпуклым называют многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящий через две его соседние вершины.
Или же другой вариант определения:
Выпуклым называют многоугольник, в котором соблюдается следующее условие: если выбрать две произвольных точки, лежащих внутри фигуры, и соединить их отрезком, то все точки этого отрезка так же будут лежать внутри многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примеры
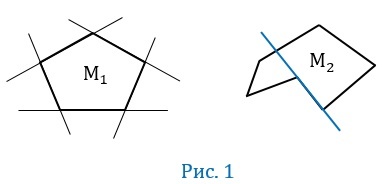
Многоугольник \(М_1\) — выпуклый, а \(М_2\) — не выпуклый.
Сумма углов выпуклого многоугольника
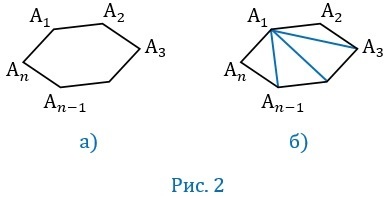
\(A_1A_2A_3. A_n\) — выпуклый многоугольник. Найдем сумму его углов:
\(\angle A_nA_1A_2,\;\angle A_1A_2A_3,\;\angle A_
Сумма внешних углов выпуклого многоугольника
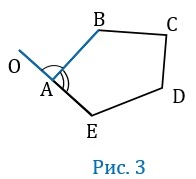
\(\angle OAD\) — внешний угол многоугольника ABCDE при вершине А. (смежный с \(\angle BAE\) )
\(180^\circ-A_1+180^\circ-A_2+. +180^\circ-A_n=n\cdot180^\circ-(A_1+A_2+. +A_n)=n\cdot180^\circ-(n-2)\cdot180^\circ=n\cdot180^\circ-n\cdot180^\circ+2\cdot180^\circ=360^\circ\)
Выпуклый многоугольник
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
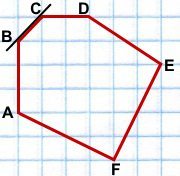
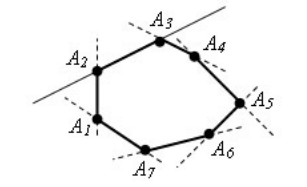
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
Важнейшие виды выпуклых многоугольников
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
    |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
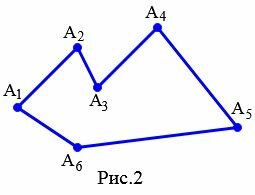 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
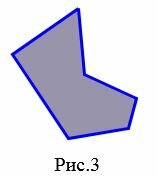 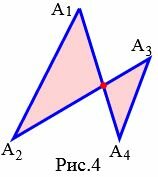 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
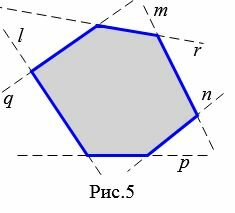 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
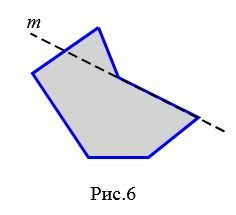 |
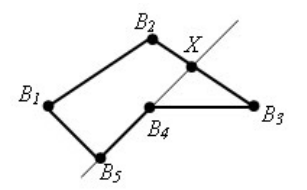
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
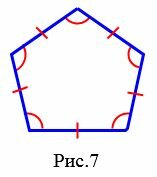 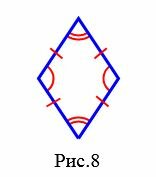 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
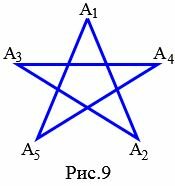 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
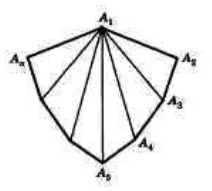
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
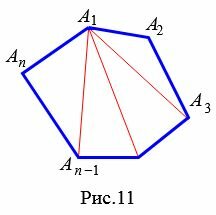 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Выпуклый многоугольник
Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Содержание
Определения
Существует множество эквивалентных определений:
Примеры
Вариации и обобщения
См. также
Полезное
Смотреть что такое «Выпуклый многоугольник» в других словарях:
выпуклый многоугольник — ▲ многоугольник ↑ выпуклый выпуклый многоугольник каждый внутренний угол меньше двух прямых; расположен в одной полуплоскости относительно любой прямой, содержащей его сторону. равносторонний. равноугольный многоугольник. изогон … Идеографический словарь русского языка
ВЫПУКЛЫЙ МНОГОУГОЛЬНИК — плоское выпуклое множество, граница к рого ломаная линия, состоящая из конечного числа прямолинейных отрезков. Иногда В. м. наз. только его границу. В. м. есть пересечение конечного числа (замкнутых) полуплоскостей. М … Математическая энциклопедия
Многоугольник — У этого термина существуют и другие значения, см. Многоугольник (значения). Примеры многоугольников Многоугольник это геометрическая фигура, обычно оп … Википедия
МНОГОУГОЛЬНИК — 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
Правильный многоугольник — выпуклый Многоугольник с равными сторонами и углами … Большая советская энциклопедия
Звёздчатый многоугольник — Звёздчатый многоугольник многоугольник, вершины которого расположены как у некоторого правильного многоугольника и стороны которого пересекаются между собой. Существует множество правильных звёздчатых многоугольников (или просто звёзд),… … Википедия
ПЛАНИГОН — выпуклый многоугольник правильного разбиения плоскости на равные многоугольники, т. е. такого разбиения, что существует группа движений плоскости, совмещающая разбиение с собой, к рая действует транзитивно на совокупности многоугольников… … Математическая энциклопедия
Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри … Википедия
Многоугольник, выпуклый многоугольник, четырехугольник
Вы будете перенаправлены на Автор24
Понятие многоугольника
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
Виды многоугольников
Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).
Рисунок 1. Выпуклый многоугольник
Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 2).
Рисунок 2. Невыпуклый многоугольник
Сумма углов многоугольника
Доказательство.
Теорема доказана.
Готовые работы на аналогичную тему
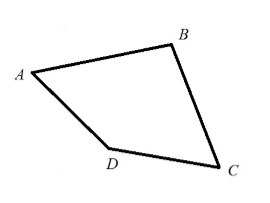
Понятие четырехугольника
Рисунок 4. Четырехугольник
Для четырехугольника аналогично определены понятия выпуклого четырехугольника и невыпуклого четырехугольника. Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм (рис. 5).
Рисунок 5. Выпуклые четырехугольники
Доказательство.
Следовательно, сумма углов выпуклого четырехугольника равняется
Теорема доказана.
Примеры задач
Определить сумму углов выпуклого девятиугольника, семиугольника и двенадцатиугольника.
Решение.
Сумма углов выпуклого пятиугольника равняется
Сумма углов выпуклого девятиугольника равняется
Сумма углов выпуклого двенадцатиугольника равняется
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 05 2021