Что такое выпуклый пятиугольник
Пятиугольник, виды, свойства и формулы
Пятиугольник, виды, свойства и формулы.
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник, выпуклый и невыпуклый пятиугольник:
Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.
Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).
Пятиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый пятиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 540°.
Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.
Рис. 2. Невыпуклый пятиугольник
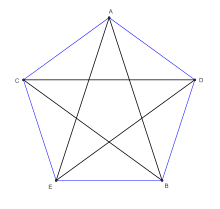
Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.
Правильный многоугольник:
Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.
Рис. 3. Правильный пятиугольник
Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.
Свойства правильного пятиугольника:
1. Все стороны правильного пятиугольника равны между собой.
2. Все углы равны между собой и каждый угол равен 108°.
Рис. 4. Правильный пятиугольник
3. Сумма внутренних углов правильного пятиугольника равна 540°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.
Рис. 5. Правильный пятиугольник
5. Количество диагоналей правильного пятиугольника равно 5.
Рис. 6. Правильный пятиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр пятиугольника O.
Рис. 7. Правильный пятиугольник
7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
Рис. 8. Правильный пятиугольник
8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
Рис. 9. Правильный пятиугольник
Построение правильного пятиугольника:
Метод построения правильного пятиугольника вписыванием его в заданную окружность:
1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.
2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
4. Постройте точку C посередине между O и B.
5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
9. Постройте правильный пятиугольник AEGHF.
Формулы правильного пятиугольника:
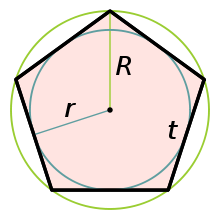
Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.
Формулы площади правильного пятиугольника:
Формулы высоты правильного пятиугольника:
Формулы стороны правильного пятиугольника:
Формулы диагонали правильного пятиугольника:
Формулы радиуса окружности, вписанной в правильный пятиугольник:
Формулы радиуса окружности, описанной вокруг правильного пятиугольника:
Правильный пятиугольник в природе, технике и культуре:
Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.
Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.
Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.
Правильный выпуклый пятиугольник
| Правильный выпуклый пятиугольник | |
 Правильный выпуклый пятиугольник (черный), его описанный круг (серый), сегменты, соединяющие его центр с его вершинами (серым), и его замечательные углы: внутренний угол (черный), внешний угол (серый). | |
| Тип | Правильный выпуклый многоугольник |
|---|---|
| Символ Шлефли | |
| Диаграмма Кокстера-Дынкина |    |
| Группа симметрии | Двугранный (D 10 ) |
| Внутренний угол | 108 ° |
| Характеристики | Сборный |
редактировать  | |
Резюме
Общий
Характеристики
Они не зависят от размера пятиугольника.
Размеры в зависимости от стороны
034> 
Некоторые характеристики правильного выпуклого пятиугольника со стороной a :
a = \ приблизительно 0,851
a \ приблизительно 1,618
a \ приблизительно 0,951
a \ приблизительно 0,951
а>
Размеры как функция радиуса описанной окружности
R \ приблизительно 1,176
R \ приблизительно 1,902
R \ приблизительно 1,118
R \ приблизительно 0,691
R>
Использует
Мощение
Два правильных пятиугольника и выпуклый десятиугольник, пересекающиеся в одной вершине; такая конфигурация не позволяет проложить план.
В гиперболической геометрии можно равномерно вымостить плоскость правильными пятиугольниками, заставив по крайней мере 4 пятиугольника пересекаться вокруг каждой вершины.
Равномерное мощение гиперболической плоскости пятиугольниками, по 4 пересечения в каждой вершине.
Гиперболическая плитка с 5 пятиугольниками вокруг каждой вершины.
Гиперболическая мостовая с 6-ю пятиугольниками вокруг каждой вершины.
Многогранники
Среди многогранников, состоящих из правильных выпуклых пятиугольников, и не исчерпывающе:
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
  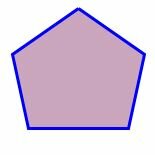  |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
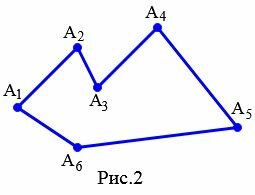 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
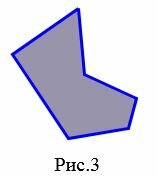 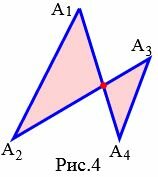 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
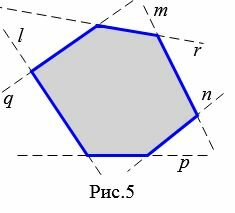 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
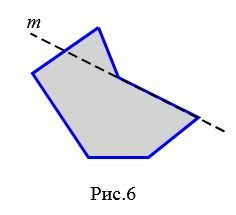 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
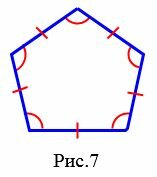 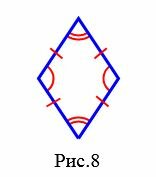 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
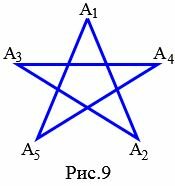 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
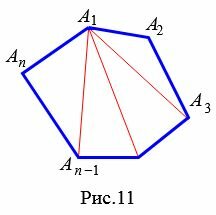 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Пятиугольник
Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.
Сумма внутренних углов выпуклого пятиугольника равна 540°.
Если провести в пентагоне диагонали, то он разобьётся на [1] :
При соединении двух первых и двух вторых треугольников их основаниями, то получится два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (был назван плитками Пенроуза).
См. также
Примечания
Планигон
Полезное
Смотреть что такое «Пятиугольник» в других словарях:
ПЯТИУГОЛЬНИК — ПЯТИУГОЛЬНИК, пятисторонняя фигура на плоскости. Сумма его внутренних УГЛОВ равна 540°. Пятиугольник, у которого все стороны и все внутренние углы равны (каждый угол равен 108°) называется правильным … Научно-технический энциклопедический словарь
ПЯТИУГОЛЬНИК — ПЯТИУГОЛЬНИК, а, муж. Геометрическая фигура, ограниченная пятью пересекающимися прямыми, образующими пять внутренних углов, а также всякий предмет такой формы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
пятиугольник — пентагон Словарь русских синонимов. пятиугольник сущ., кол во синонимов: 2 • многоугольник (12) • … Словарь синонимов
ПЯТИУГОЛЬНИК — ПЯТИУГОЛЬНИК, пятиугольника, муж. (мат.). Многоугольник с пятью углами. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
пятиугольник — (5 угольник) … Орфографический словарь-справочник
пятиугольник — ПЯТИУГОЛЬНИК1, а, м Предмет, имеющий форму геометрической фигуры, ограниченной пятью пересекающимися прямыми, образующими пять внутренних углов. Корпус здания был выстроен пятиугольником. Профессор играючи начертил мелом на доске правильный… … Толковый словарь русских существительных
Пятиугольник — м. 1. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей пять углов. 2. Пространство или предмет такой формы. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
пятиугольник — пятиугольник, пятиугольники, пятиугольника, пятиугольников, пятиугольнику, пятиугольникам, пятиугольник, пятиугольники, пятиугольником, пятиугольниками, пятиугольнике, пятиугольниках (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов
пятиугольник — пятиуг ольник, а … Русский орфографический словарь