Что такое выпуклый многоугольник 8 класс определение
Какой многоугольник называется выпуклым
Что такое выпуклый многогольник
Выпуклым называют многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящий через две его соседние вершины.
Или же другой вариант определения:
Выпуклым называют многоугольник, в котором соблюдается следующее условие: если выбрать две произвольных точки, лежащих внутри фигуры, и соединить их отрезком, то все точки этого отрезка так же будут лежать внутри многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примеры
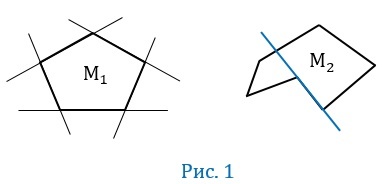
Многоугольник \(М_1\) — выпуклый, а \(М_2\) — не выпуклый.
Сумма углов выпуклого многоугольника
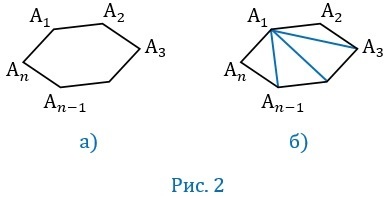
\(A_1A_2A_3. A_n\) — выпуклый многоугольник. Найдем сумму его углов:
\(\angle A_nA_1A_2,\;\angle A_1A_2A_3,\;\angle A_
Сумма внешних углов выпуклого многоугольника
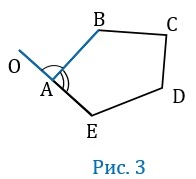
\(\angle OAD\) — внешний угол многоугольника ABCDE при вершине А. (смежный с \(\angle BAE\) )
\(180^\circ-A_1+180^\circ-A_2+. +180^\circ-A_n=n\cdot180^\circ-(A_1+A_2+. +A_n)=n\cdot180^\circ-(n-2)\cdot180^\circ=n\cdot180^\circ-n\cdot180^\circ+2\cdot180^\circ=360^\circ\)
8 класс. Геометрия. Многоугольники.
8 класс. Геометрия. Многоугольники.
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
Многоугольники
1. Понятие «многоугольник»
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах – многоугольниках.
С частным случаем многоугольников мы уже знакомы – это треугольник (см. Рис. 1).
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение.Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение.Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят кмногоугольнику.
Иными словами, например, когда говорят о пятиугольнике 
, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т.е. точка 
тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника – сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.
Рис. 3. Невыпуклый многоугольник
2. Выпуклые и невыпуклые многоугольники
Определение 1. Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через 
в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым, если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков 
на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
3. Теорема о сумме внутренних углов выпуклого n-угольника
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника. Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
, где 
– количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
Рис. 4. Выпуклый n-угольник
Из вершины 
проведем все возможные диагонали. Они делят n-угольник на 
треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника – 
, то сумма внутренних углов n-угольника:
, что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол 
. Имеем:
, что и требовалось доказать.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике 
, а сумма углов 
. В четырехугольнике 
, а сумма углов – 
и т.д.
4. Теорема о сумме внешних углов выпуклого n-угольника
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
, где – количество его углов (сторон), а 
, …, 
– внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.
Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то 
и аналогично для остальных внешних углов. Тогда:
.
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника 
.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна 
от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Далее мы более подробно будем работать с частным случаем многоугольников – четырехугольниками. На следующем уроке мы познакомимся с такой фигурой, как параллелограмм, и обсудим его свойства.
Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.
Многоугольник называется выпуклым если:
Определение I — для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём.
Определение II — каждый внутренний угол меньше 180°.
Определение III — все его диагонали полностью лежат внутри него.
Определение IV – он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n-2)∙180°.
Сумма углов невыпуклого n-угольника также равна (n-2)∙180°. (Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники).
Теорема: Число диагоналей всякого n-угольника равно 
.
Задача*: в каком выпуклом многоугольнике диагоналей на 25 больше чем сторон?
р = 25+n
25+n = 
Разложим на множители
(n+5)(n-10)=0
n=-5 не удовлетворяет,
так как не существует
n = 10 удовлетворяет
Ответ: Десяти угольник.
Фигуры с равными диагоналями.*
Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.
Две несмежные стороны называются противоположными.
Две не соседние вершины называются противоположными.
1) Противоположные стороны параллелограмма равны. AB=DC, AD=BC.
2) Противоположные углы параллелограмма равны. ÐA=ÐC, ÐB=ÐD.
3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD.
4) Сумма углов, прилежащих к одной стороне, равна 180°. ÐA+ÐD=180°, ÐA+ÐB=180°, ÐB+ÐC=180°, ÐD+ÐC=180°.
5) Сумма всех углов равна 360°. ÐA+ÐB+ÐC+ÐD=360°.
6)* Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: AC2+BD2=2∙(AB2+AD2).
Задача 1*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна AC=9 см, а стороны AD=7 см и AB=4 см.
Решение: Подставив значения в формулу получим:
BD2=49, следовательно вторая диагональ равна BD=7 см. Ответ: 7 см.
Задача 2*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна BD=10 см, а стороны AD=8 см и AB=2 см.
Решение: Условия задачи не верно, так как сумма двух сторон треугольника всегда больше третей стороны. Ответ: задача не имеет решений (смысла).
Задача 3*: а)Найти сторону параллелограмма, если известно, что длина диагоналей равна BD=6 см, AC=8, а одна сторона AB=5 см. б)Как называется этот параллелограмм.
Задача 4**: Сумма длин диагоналей параллелограмма равна 12 см, а произведение 32 найдите значение суммы квадратов всех его сторон.
Задача 5**:Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.
Решение: Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб.
Действительно, пусть a и b – длины соседних сторон параллелограмма, а 
и 
– длины его диагоналей (см. рис. 2). Тогда периметр параллелограмма: P = 2(a + b).
Из равенства 
, выражающего теорему о сумме квадратов диагоналей параллелограмма, следует, что у всех параллелограммов с данными диагоналями сумма квадратов сторон есть величина постоянная.
По неравенству между средним арифметическим и средним квадратичным: 
Û 
, причем равенство достигается т. и т. т., когда a = b. Значит, параллелограмм с наибольшим периметром является ромбом. Находим сторону этого ромба: 
=5(см). Ответ: 20 см.
Определение 2: это четырёхугольник, у которого все углы прямые.
Определение 3: это параллелограмм, у которого один угол прямой.
Свойства прямоугольника: те же свойства, что и у параллелограмма +
1) Диагонали прямоугольника равны.
2)* Квадрат диагонали равен сумме квадратов сторон.
Задача 1: Меньшая сторона прямоугольника равна 5см, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
Задача 2: Меньшая сторона прямоугольника равна 24, диагонали пересекаются под углом 120°. Найдите диагонали и большую сторону прямоугольника.
Задача 3*: Сторона прямоугольника равна 3 см, диагональ 5 см. Найдите другую сторону прямоугольника.
Задача 4*: Сторона прямоугольника равна 6 см, диагональ 10 см. Найдите площадь прямоугольника.
Определение 2: это четырёхугольник, у которого все стороны равны.
Свойства ромба: те же свойства, что и у параллелограмма +
1) Диагонали ромба взаимно перпендикулярны (AC ⊥ BD).
3)*Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
Задача 1: Диагонали ромба 6 и 8 см. Найти сторону ромба.
Задача 2: Сторона ромба 10 см, один из углов 60°. Найти маленькую диагональ ромба.
Урок геометрии на тему «Многоугольники». 8-й класс
Класс: 8
Презентация к уроку
Учебник: Геометрия. 7–9 классы: учеб. для общеобразоват. учреждений / [Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.]. – М.: Просвещение.
Оборудование: компьютер, проектор, экран
Ход урока
Рассмотрим фигуру, составленную из отрезков A1 A2; A2 A3;…; An-1 An (рис. 1–3). Точки A1 и An могут быть различными, а могут совпадать. Соседние отрезки не лежат на одной прямой. Такая фигура называется ломаной, а отрезки, из которых она состоит – звеньями.
— Как вы думаете, на каком рисунке изображена замкнутая ломаная?
— На каких рисунках ломаная простая?
Ломаная называется простой, если ее несоседние звенья не имеют общих точек.
Простая замкнутая ломаная называется многоугольником.
Любой многоугольник разделяет плоскость на внутреннюю и внешнюю области.
Сумма длин всех сторон называется периметром многоугольника.
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
— Какие из фигур, изображенных на рисунке, являются многоугольниками?
— Изобразите многоугольники в тетради и отметьте точки во внешней и внутренней областях многоугольника.
2. Выпуклые и невыпуклые многоугольники
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Выпуклый многоугольник Невыпуклый многоугольник
— Назовите номера выпуклых многоугольников
— Перечертите любой выпуклый многоугольник в тетрадь и обозначьте его вершины
Задание. Начертите выпуклый восьмиугольник и проведите все его диагонали из какой-нибудь вершины. Сколько при этом получилось треугольников? Найдите сумму углов восьмиугольника.
Получилось шесть треугольников, то есть 
— Как вы думаете, как вычислить сумму углов выпуклого n-угольника?
— 
Задача. Можно ли выпуклый стоугольник разрезать на 97 треугольников?
Решение. 
— сумма углов стоугольника
— сумма углов треугольника
Ответ: выпуклый стоугольник разрезать на 97 треугольников нельзя.
Этот материал учащиеся осваивают самостоятельно (п. 41 учебника).
4. Если есть время, то можно предложить учащимся выполнить упражнения 364(а); 365 (а; б) учебника.
Домашнее задание. П. 39–41. № 363; 364(б); 365(в)
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.