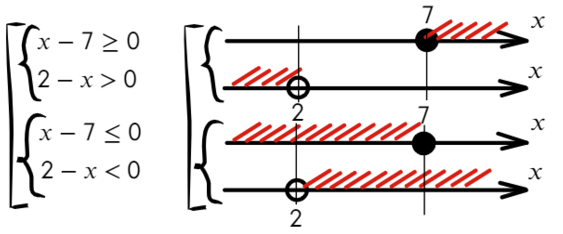
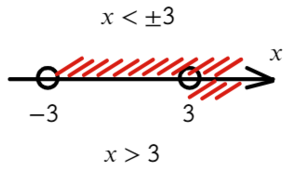
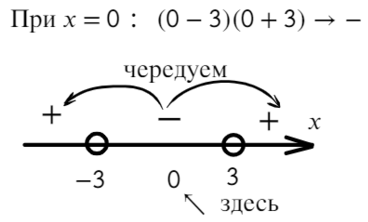
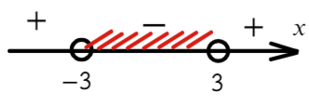
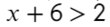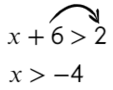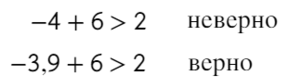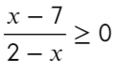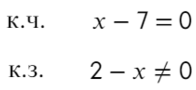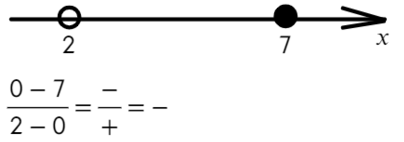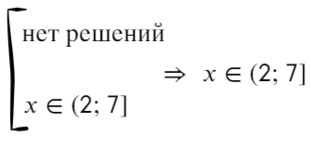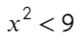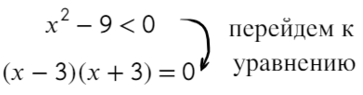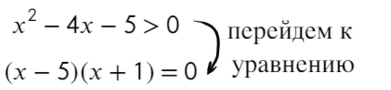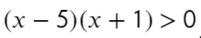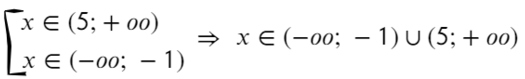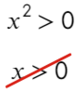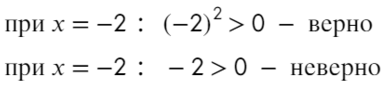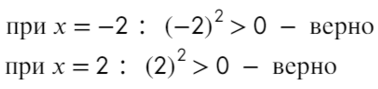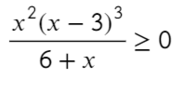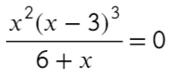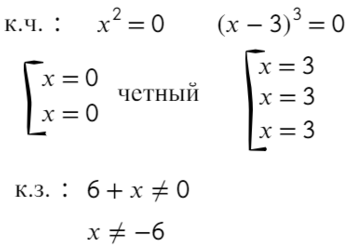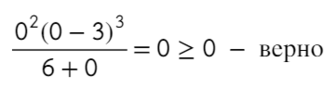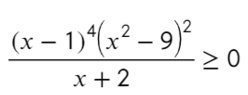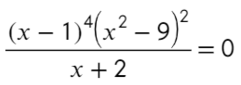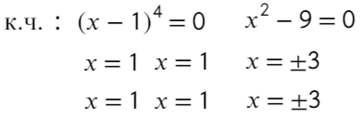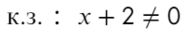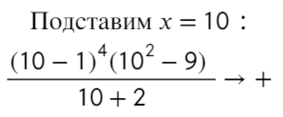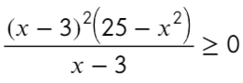Что такое выколотая точка
Как пересекать промежутки?
Операции над числовыми промежутками.
Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?
Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…
Как пересекать промежутки?
Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.
Итак, для начала запоминаем:
Пересечением двух числовых промежутков называется их общая часть.
И всё! Смутить могут только слова «общая часть». Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова «общая часть» и «одновременно» здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)
Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:
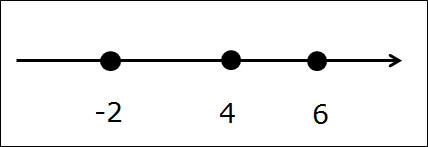
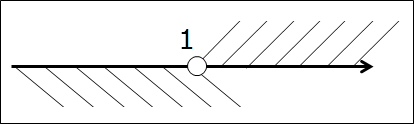
Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:
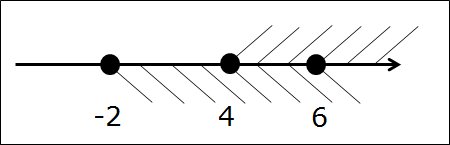
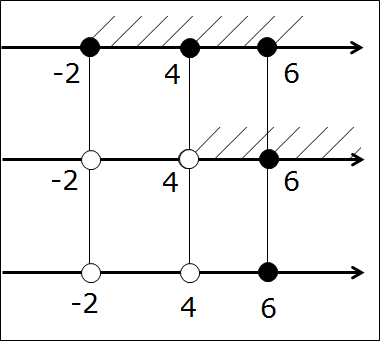
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя «ёлочку», но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:
А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)
Математически результат пересечения оформляют вот так:
[-2; 6] ⋂ [4; +∞) = [4; 6]
Значок «⋂» означает «пересечение».
Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)
Пересечём, например, промежутки:
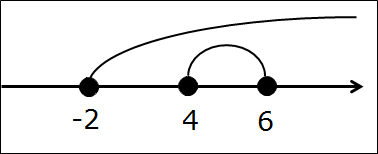
Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:
И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?
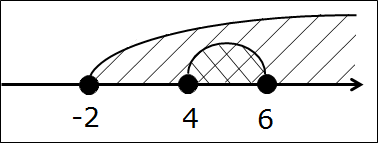
Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:
Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.
В математической форме:
[-2; +∞) ⋂ [4; 6] = [4; 6]
Уловили идею? Ну-ка, быстренько закрепим успех!
Найдите пересечения следующих числовых промежутков:
Ответы (в беспорядке):
Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)
Сюрприз первый — пустое множество
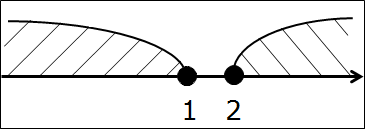
Попробуем пересечь, скажем, такие два промежутка:
(-∞; 1] ⋂ [2; +∞)
Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…
И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.
Математически эта фишка записывается вот как:
(-∞; 1] ⋂ [2; +∞) = Ø
Этот перечёркнутый кружочек означает «пустое множество». Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.
Сюрприз второй — изолированная точка
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:
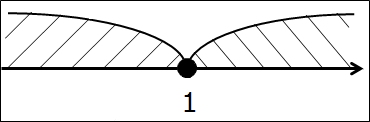
(-∞; 1] ⋂ [1; +∞)
Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.
А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.
В таких случаях результат пересечения (одна точка) оформляют так:
(-∞; 1] ⋂ [1; +∞) =
Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.
Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)
Кто читает вдумчиво, тот заметил, что слово «множество» я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется «Теория множеств» и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…
Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:
Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:
(-∞; 1] ⋂ [0; 2] = [0; 1].
Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.
Проблемы начинаются с появлением выколотых точек.
Как работать с выколотыми точками?
Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…
Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?
Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.
А пока фиксируем в памяти одну простую вещь:
Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.
Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?
Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:
[-2; 6] ⋂ [4; +∞)
А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:
[-2; 6] ⋂ (4; +∞)
Рисуем, штрихуем, получаем картинку:
Ищем общую часть, записываем ответ:
[-2; 6] ⋂ (4; +∞) = (4; 6]
Кто в теме и врубился в слова «общая часть» и «одновременно», тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:
А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].
Итого: (4; 6].«
Вот так. Я же говорил, что ключевое слово здесь — одновременно!
Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:
(-∞; 1) ⋂ [1; +∞)
Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.
И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…
Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!
Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.
Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:
(-∞; 1) ⋂ [1; +∞) = Ø
Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.
Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)
Обещанный секретный способ!
Пересекаем промежутки без ошибок! Метод параллельных осей.
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).
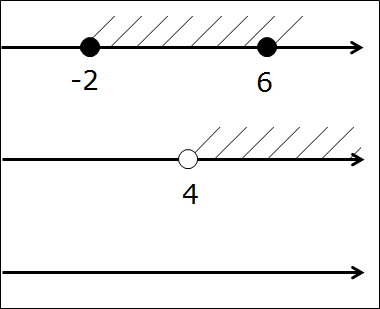
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:
Представили? Вот так:
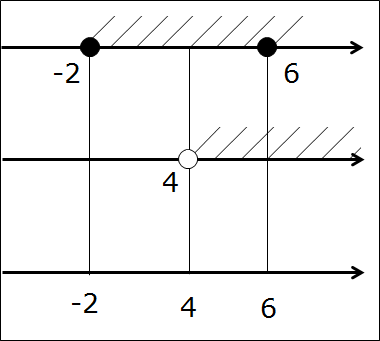
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!
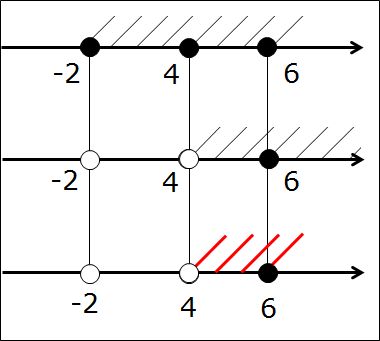
Картинка станет вот такой:
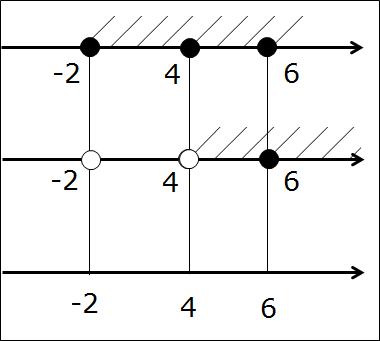
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:
Ответ: (4; 6]
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)
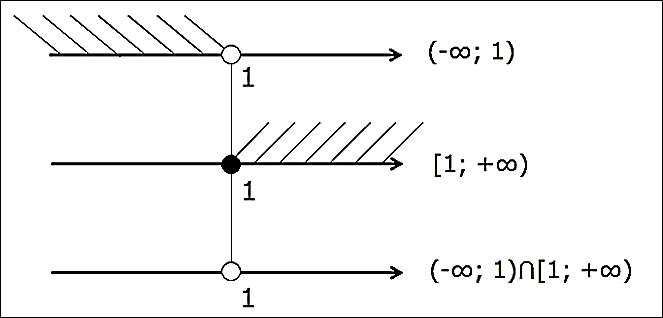
Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:
Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…
Ответ: Ø
Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…
Закрашенная и незакрашенная точка
Знание — сила. Познавательная информация
Выколотая точка или закрашенная?
Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
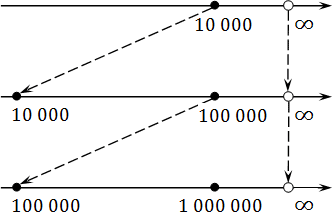
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
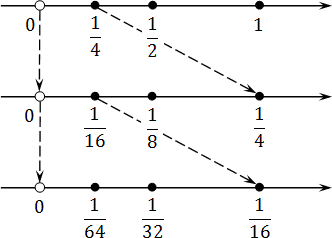
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
 Решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
А само значение −4 нам подходит?
Нет, поэтому ставим круглые скобочки ()
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
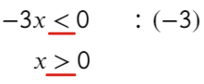
Следующий пример уже с дробью:
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
к.ч. (корни числителя)
к.з. (корни знаменателя)
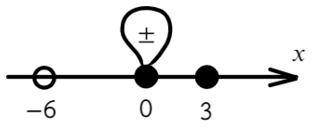
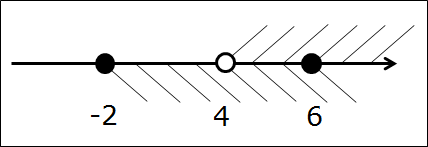
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
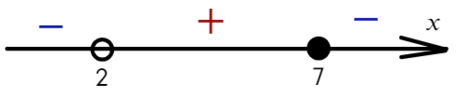
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
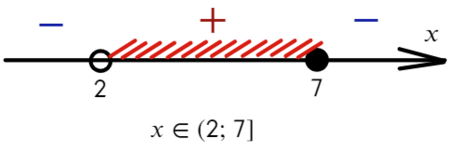
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
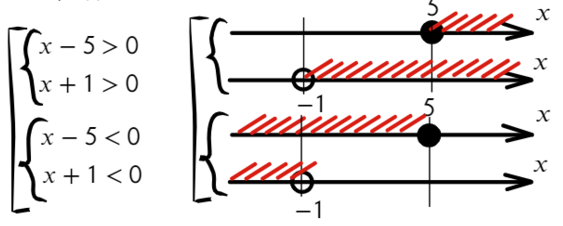
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
Отметим на прямой решение каждого неравенства.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
Мой любимый пример:
Покажу мастер-класс, как делать не надо. Дома не повторять!
А теперь через метод интервалов разберемся, как сделать правильно:
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
Перейдем к квадратному уравнению:
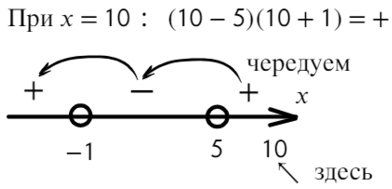
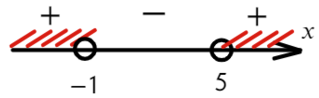
Разложим на множители и подставим x = 10, чтобы определить знак:
Нам требуются положительные значения:
Второй способ разложить на множители:
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
А теперь простой, но крайне показательный пример:
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:
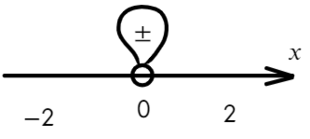
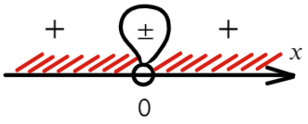
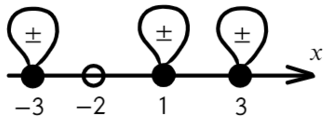
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».
Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R или x ∈ ( − oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
По методу координат найдем корни числителя и знаменателя:
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).
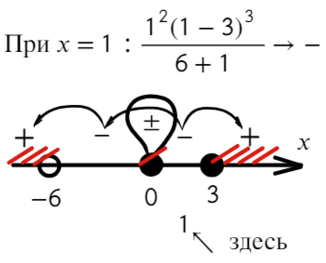
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ ∪ [ 3; +oo).
По той же схеме корни числителя и знаменателя:
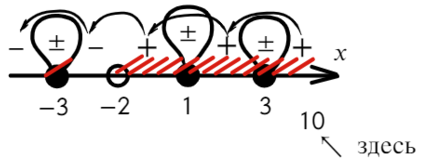
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
Подставим x = 10 и расставим знаки:
Ответ: [ −oo; −5) ∪ [ 3; 5).
Все скользкие моменты разобрали, стало понятнее?
Группа с полезной информацией и легким математическим юмором.
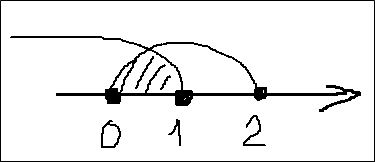
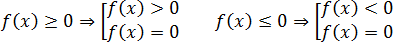

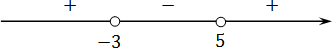
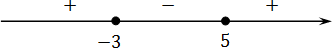
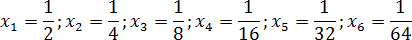
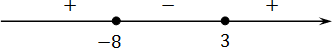
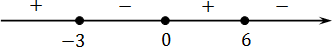
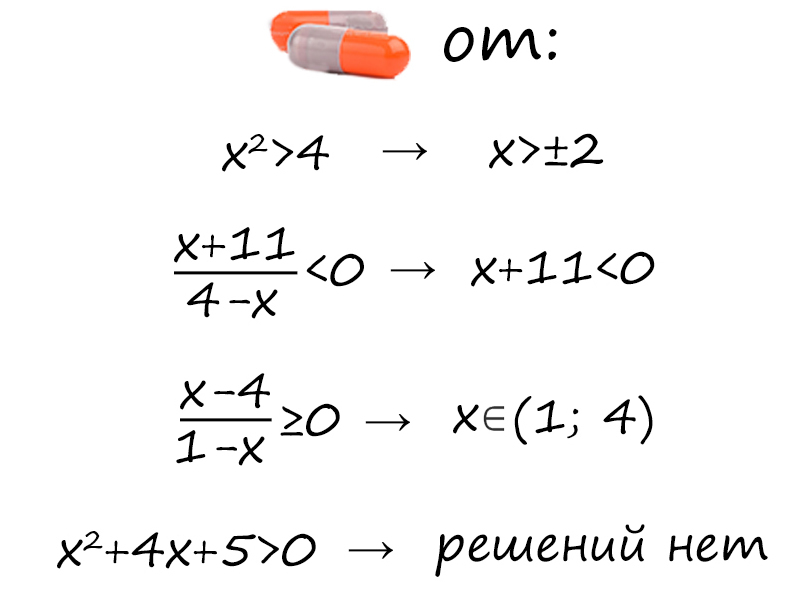 Решение неравенств
Решение неравенств