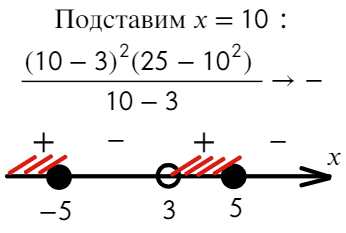
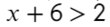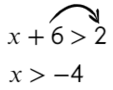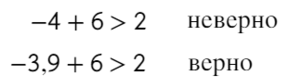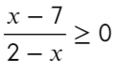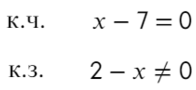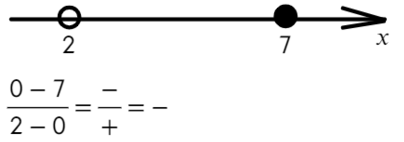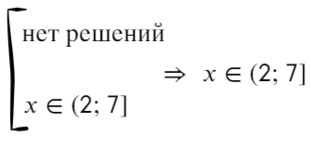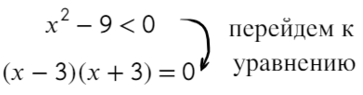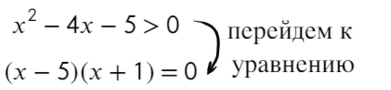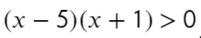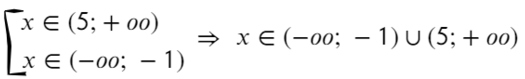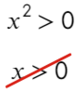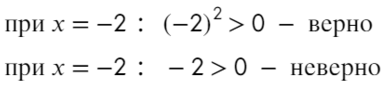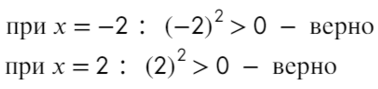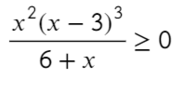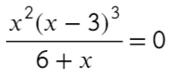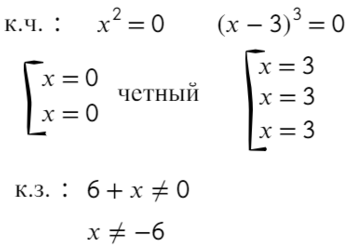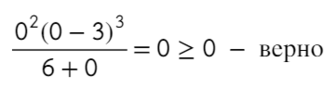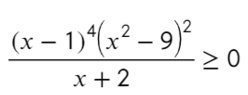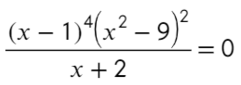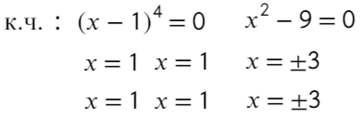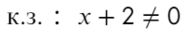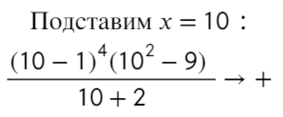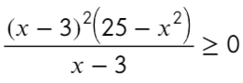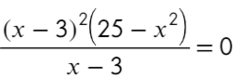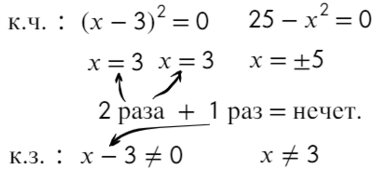Что такое выколотая точка на графике функции и зачем она нужна
Закрашенная и незакрашенная точка
Знание — сила. Познавательная информация
Выколотая точка или закрашенная?
Эта ассоциация поможет легко запомнить, выколотая точка или закрашенная на числовой прямой.
Сравните неравенства, при которых точка заштрихована: x≥a или x≤b и неравенства, в которых точка выколотая: x>a, x или Светлана Иванова, 27 Сен 2012
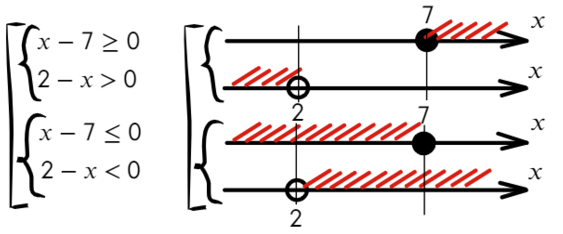
Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:
— это неравенство вида которое равносильно совокупности строгого неравенства и уравнения:
В переводе на русский язык это значит, что нестрогое неравенство это объединение классического уравнения и строгого неравенства Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.
Отрезки и интервалы: в чем разница?
Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:
Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:
На этом рисунке отмечен отрезок и интервал Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.
Метод интервалов для нестрогих неравенств
К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:
Задача. Решите строгое неравенство:
Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
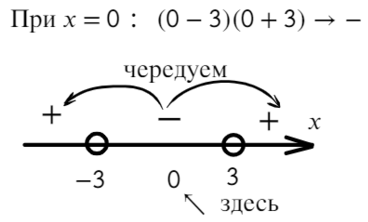
Отмечаем полученные корни на координатной оси:
Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:
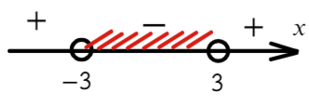
Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:
Задача. Решите нестрогое неравенство:
Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:
( x − 5)( x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;
Отмечаем полученные корни на координатной оси:
В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:
Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:
Итак, основное отличие строгих и нестрогих неравенств:
Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.
Почему бесконечности всегда стоят в круглых скобках
У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем
Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.
— это гипотетическое число, которое больше любого другого числа, участвующего в решении.
Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.
Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.
Ситуация такая же, как с границами интервалов. Рассмотрим все числа из интервала:
Эта запись означает, что число не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:
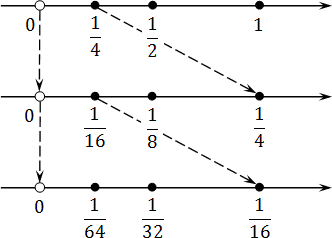
Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим вроде этого:
Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.
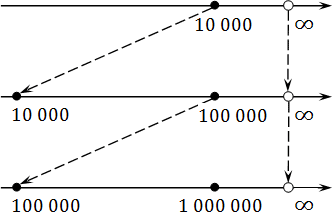
То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:
Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.
Примеры решения неравенств
В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.
Как обычно, приравниваем все к нулю:
( x + 8)( x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.
Теперь рассматриваем функцию, которая находится в левой части неравенства:
Подставим в эту функцию бесконечность — получим выражение вида:
Чертим координатную ось, отмечаем корни и расставляем знаки:
Поскольку мы решаем неравенство или, что то же самое, осталось записать ответ:
x (12 − 2 x )(3 x + 9) ≥ 0
x (12 − 2 x )(3 x + 9) = 0;
x = 0;
12 − 2 x = 0 ⇒ 2 x = 12 ⇒ x = 6;
3 x + 9 = 0 ⇒ 3 x = −9 ⇒ x = −3.
x ≥ 6 ⇒ f ( x ) = x (12 − 2 x )(3 x + 9) → (+) · (−) · (+) = (−) x ∈ (−∞ −3] ∪ [0; 6].
 Решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
А само значение −4 нам подходит?
Нет, поэтому ставим круглые скобочки ()
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие ( ≥, ≤ ), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
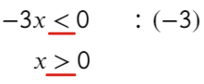
Следующий пример уже с дробью:
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
к.ч. (корни числителя)
к.з. (корни знаменателя)
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
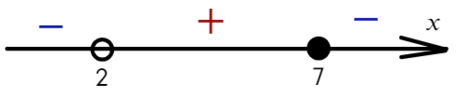
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
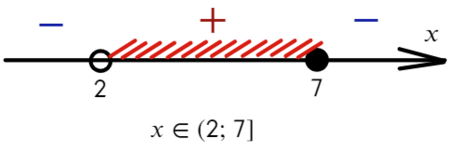
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>,
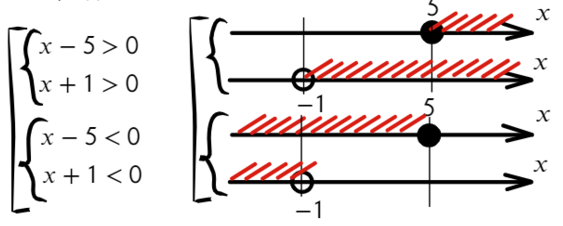
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
Отметим на прямой решение каждого неравенства.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
Мой любимый пример:
Покажу мастер-класс, как делать не надо. Дома не повторять!
А теперь через метод интервалов разберемся, как сделать правильно:
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
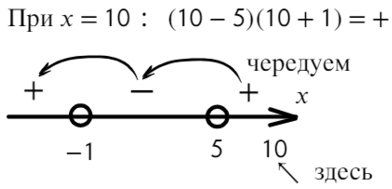
Перейдем к квадратному уравнению:
Разложим на множители и подставим x = 10, чтобы определить знак:
Нам требуются положительные значения:
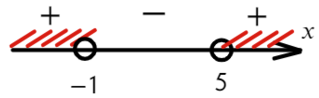
Второй способ разложить на множители:
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
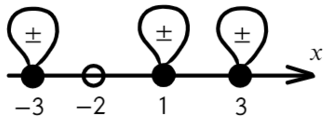
А теперь простой, но крайне показательный пример:
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:
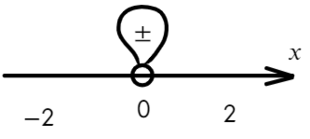
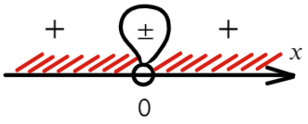
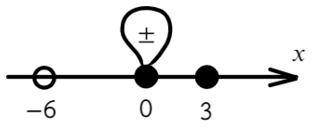
Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».
Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R или x ∈ ( − oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
По методу координат найдем корни числителя и знаменателя:
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).
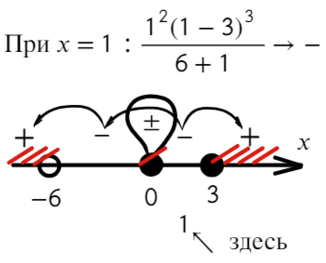
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ ∪ [ 3; +oo).
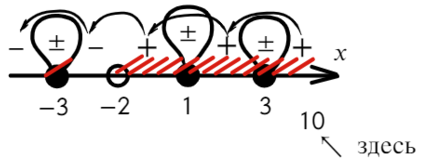
По той же схеме корни числителя и знаменателя:
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
Подставим x = 10 и расставим знаки:
Ответ: [ −oo; −5) ∪ [ 3; 5).
Все скользкие моменты разобрали, стало понятнее?
Группа с полезной информацией и легким математическим юмором.
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Что такое выколотая точка на графике функции и зачем она нужна
Введение. Размышляя о точке [1], мы сознательно не заостряли внимания на её разнообразных представлениях в математике. Тема обширная, достаточно изученная и одновременно понятная. Во всяком случае, в терминологическом плане.
Поэтому вполне закономерно и справедливо появление отдельных высказываний и дополнений по затронутой нами тематике. Прежде всего, речь идет о небольшой заметке [2], которая через предложенную библиографию существенно расширяет ракурс восприятия. Упомянутые литературные источники широко используют известные математические понятия, однако, в собственной трактовке-интерпретации. Для чего это нужно, не совсем понятно. Тем более на фоне главной линии: создать семантический образ христианской троицы. В результате, появляются отдельные совсем необязательные разногласия с установившейся терминологией, которые непроизвольно порождают элементы путаницы.
Предельная точка. В математике различают разные точки: особые, изолированные, предельные, выколотые, точки разрыва (первого и второго рода), точки касания и другие. С позиций автора [2]: «»Предельная Точка» есть форма кардинального взаимного полагания трех не сводимых друг к другу уникальных параметров: предельной формы скрытого источника, предельной формы операнда и предельной формы оператора».
Ранее в его исследованиях звучала «особая выколотая точка» (об этом ниже), и теперь вдруг без пояснений – «предельная», как конгломерат трех разнородных предельных форм.
Напомним, точка x0 – предельная точкой множества E, если в произвольной окрестности точки x0 существует хотя бы одна точка из E, отличная от x0. Так, любая (!) точка единичного шара (без точек поверхности) <x : |x| r – кольцевой тор.
Полноторий (твердый или сплошной тор) – топологическое пространство, трехмерное геометрическое тело, ограниченное тором. Неформально, полноторий – бублик, тор – его поверхность, например пустотелая камера колеса.
В интерпретации автора «тор занимает всё пространство», следовательно, предметом рассмотрения является полноторий.
Вырожденность. В математике вырожденными называют объекты, обладающие принципиально более простой структурой и смыслом по сравнению с остальными объектами в своем классе. Даже если их взять вместе, они не дадут полного представления обо всём классе. «Вырожденный» означит особенный случай.
Так, три вершины вырожденного треугольника лежат на одной прямой. Квадратное уравнение (х – 1) 2 = 0 имеет один корень х = 1. При R = 0 тор вырождается в сферу, при r = 0 – в окружность, образуя
след от движущейся точки (r = 0) вокруг центра на расстоянии R.
«Предельно вырожденный тор». – В чём конкретно выражается его вырожденность, из авторских статей неясно. Равно как и в чём состоит предельность? – Если R → ∞, то это скорее беспредельное расширение модели в пространстве. Спрашивается, какие цели при этом достигаются? – Ведь основную идею можно показать и для R = r = 1.
Вырожденность вообще смещает акценты в сторону меньшей репрезентативности, сводя тор до уровня окружности и/или иной топологии, когда становится ненужным сам тор.
Выколотая точка (ВК) – безусловно, красивый термин и прекрасное дополнение к общей классификации всевозможных точек.
Формально выколотую точку b можно выразить с помощью неравенства x > b.
Выколотая точка не лежит на графике. Значение функции в ней не существует и не рассматривается. Примером служит дробно-рациональная функция, для которой нули или корни знаменателя – выколотые точки. В этих точках функция не определена, поскольку на нуль делить нельзя. Окружность с выколотой точкой гомеоморфна прямой.
Автор отмечает: все окружности касаются друг друга в одной единственной (особой выколотой) точке – центре тора. То есть речь идет о роговом торе без «дырки» (R = r) и без центральной точки.
Обычная сфера (граница трехмерного шара) является двумерной как и всякая поверхность. Если на ней имеется одна выколотая точка, то в топологическом аспекте она становится гомотопной плоскости. Именно так образуется стереографическая проекция (конформное отображение) [5], в том числе карта Земли.
Де-факто центральная точка в торе не является выколотой. По определению. Такое свойство автор привносит искусственно, на уровне априорного положения. Из характера построения тороидальной модели выколотая точка «алгоритмически» не получается. Если этим свойством она наделяется принудительно, то так и нужно об этом говорить.
Тогда возникает вопрос: насколько это важно в принятой модели?
На наш взгляд, точка, выколотая или не выколотая, для характеристики троицы не принципиально. Главное – смысл, её содержание и внутренняя насыщенность.
Не следует также забывать, что сама по себе троица – уже некая модель божества. Одна из многих, придуманных людьми разных умонастроений и частей света. Любая модель троицы однозначно приобретает оттенок «модельной модели». И термин ВК, как часть модельного описания, здесь не вносит ясность. Троица не вмещается в рациональные конструкции. Поэтому её модельные представления, включая точку, являются некими условными картинками-иллюстрациями. Как три совмещенных нуля, три окружности и проч.
В топологии доказывается [6, с. 121], что все связные ориентируемые компактные двумерные многообразия суть сферы с n ≥ 0 ручками. Из них только тор (n = 1) допускает касательное векторное поле без особых точек. – Такое замечательное отличительное свойство, которое автор зачем-то устраняет путем введения выколотой точки.
Наоборот, эту точку, принадлежащую тору, нужно не выкалывать, а трепетно беречь, сохраняя принятую пространственную топологию. Чтобы не получить вместо тора-«бублика» окружность, а взамен объемной интерпретации – топологию плоскости.
В данной точке ось поверхности тора не имеет разрыва, сам полноторий не прерывается. Но стоит эту единственную точку удалить, как возникает ненужный топологический дефект. С переводом модели на плоскостной инвариант.
Заключение. Представляется, что в правильных поисках основательной троичной модели автор несколько перестарался в понятийном контексте. Стремление к терминологической насыщенности, напоминающей излишество, часто чревато потерей сути-канвы. Тот же «предельно вырожденный тор», вместо ясного изложения-объяснения, создает условия для возникновения противоречий. Вырожденный тор – уже не тор так таковой. В результате вырождения он теряет свои отличительные особенности, позволяющие ему таковым называться. Всё равно, что два соседних отрезка на линии настойчиво называть вырожденным треугольником. Ради чего?
Любопытным образом трактует и расшифровывает «ТОР» православный исследователь В. Говоров (АТ, публ. 23958, 15.11.2017) как тройное отношение радиусов через три последовательных действия: формирование круга, его вращение вокруг собственной оси с образованием сферы и её вращение вокруг новой оси до получения собственно тора или полнотория. Как идеально-тройственная структура, в которой совсем не обязательно принудительно «выкалывать» центральную точку (при R = r). Оное действо не является вынужденно необходимым даже для образного отображения источника божественной силы.
В целом тор, конечно, является оригинальной и прекрасной троично-иллюстративной моделью, которую предложили С. Костюченко и В. Татур. Её уточнение и развитие должны способствовать созданию красивого и непротиворечивого логико-геометрического образа. Ad primos ictus non corruit ardua quercus.
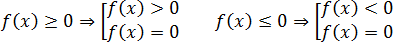

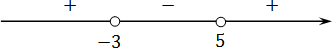
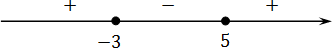
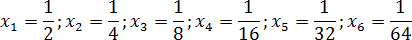
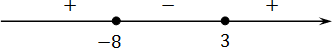
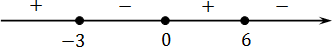
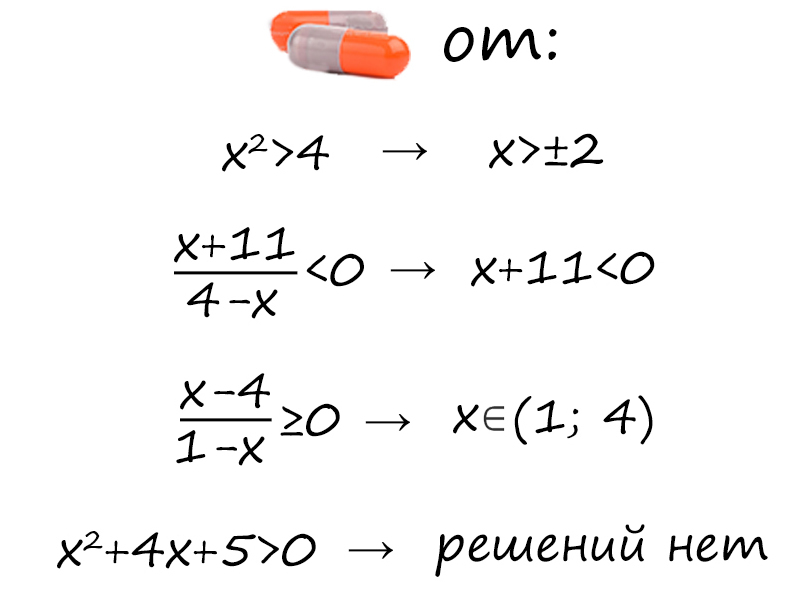 Решение неравенств
Решение неравенств