Что такое выигрышная стратегия в игре информатика
Методика решения задач ЕГЭ по информатике с использованием понятия «выигрышной стратегии»
В разработке представлены типы задач ЕГЭ по теории игр и методы их решения
Просмотр содержимого документа
«Методика решения задач ЕГЭ по информатике с использованием понятия «выигрышной стратегии»»
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ЕГЭ ПО ИНФОРМАТИКЕ И ИКТ С ИСПОЛЬЗОВАНИЕМ ПОНЯТИЯ «ВЫИГРЫШНОЙ СТРАТЕГИИ»
Выступление на республиканском семинаре «Об особенностях преподавания информатики в общеобразовательных организациях Республики Крым в 2018/2019 учебном году» 23.08.2018
Сабитова Диляра Арифовна, методист отдела дистанционного образования
ГБОУ ДПО РК КРИППО
Понятие выигрышной стратегии. Типы задач
Разбор задания № 26 демонстрационной версии ЕГЭ-2018
Разбор проекта демонстрационной версии ЕГЭ-2018. Фишки
Разбор задачи основного периода ЕГЭ-2018. Две кучи
Разбор задачи №26 системы «Эксперт ЕГЭ». Буквы
Понятие выигрышной стратегии. Типы задач
Стратегия игрока определяет его действие в любой момент игры и для каждого возможного течения игры.
Игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Разбор задания № 26 демонстрационной версии ЕГЭ-2018
Вопрос 1а. Последним ходом может быть «+1» или «*2». Выиграть последним ходом «+1» можно, если S = 28. Ходом «*2» можно выиграть из любой позиции при S 14 (сюда входит и 28). Можно составить таблицу, в которой «В1» обозначает выигрыш за один ход:
Поэтому ответ должен быть такой:
«1а. Петя может выиграть за один ход при любом S =15,…28. Он должен увеличить вдвое число камней, при этом в куче всегда получится не менее 30 камней.»
Вопрос 1б. Для ответа на этот вопрос нужно найти позицию, из которой все возможные ходы ведут к выигрышу за 1 ход, то есть к позиции, отмеченной в таблице как «В1». Например, это позиция при S = 14: ход «+1» ведёт в выигрышную позицию S = 15, а ход «*2» ведёт в выигрышную позицию S = 28. Поэтому позицию S = 14 отметим в таблице как «х1» (проигрыш за 1 ход):


Ответ на вопрос 1б должен быть такой:
«1б. При S = 14 Петя не может выиграть в один ход, потому что при его ходе «+1» число камней в куче становится равно 15 (меньше 29), а при ходе «*2» число камней в куче становится равно 28 (также меньше 29). Других возможных ходов у Пети нет. Из любой позиции после одного хода Пети (это может быть 15 или 28), Ваня может выиграть своим первых ходом, удвоив количество камней в куче.»
Вопрос 2. Пете, для того, чтобы гарантированно выиграть на втором ходу, нужно из начальной позиции перевести игру в проигрышную позицию, отмеченную знаком «х1». Пока мы нашли одну такую позицию: S = 14. Петя может перевести игру в эту позицию из позиций
S = 13 (ходом «+1») и S = 7 (ходом «*2»)


Поэтому ответ должен быть такой:
«2. Из позиций S = 7 и S = 13 Петя не может выиграть в один ход, но Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. При S = 13 ходом «+1» Пете нужно перевести игру в позицию S = 14, которая является проигрышной (см. ответ на вопрос 1б). При S = 7 Петя переводит игру в ту же позицию ходом «*2».»
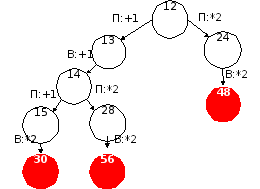
Вопрос 3. Нужно найти такую позицию, из которой оба возможных хода Пети ведут в позиции, отмеченные в таблице как «В1» (выигрыш в 1 ход) и «В2» (выигрыш в 2 хода). Например, это позиция S = 12, из которой можно «попасть» только в S = 13 («В2») и S = 24 («В1»). Отмечаем эту позицию как «х2» – проигрыш в два хода:


Поэтому ответ должен быть такой:
«3. В позиции S = 12 у Вани есть выигрышная стратегия, которая позволяет ему выиграть первым или вторым ходом. Если Петя выбирает ход «+1», в куче становится 13 камней и Ваня выигрывает на 2-м ходу (см. ответ на вопрос 2). Если Петя выбирает ход «*2», Ваня выигрывает первым ходом, удвоив число камней в куче.»
Остается нарисовать дерево возможных вариантов игры из позиции S = 12. Для этого используем построенную таблицу:
Здесь красным цветом выделены позиции, в которых игра заканчивается.
На каждом шаге мы рассматриваем все возможные ходы Пети и только один лучший ход Вани. Например, в позиции S = 15 Ваня может сделать ход «+1» и получить 16 камней в куче, но тогда он проиграет (Петя следующим ходом удвоит число камней и получит 32 камня). Этот ход мы не рассматриваем, потому что мы хотим доказать, что у Вани есть выигрышная стратегия – ему достаточно хода «*2», после которого он выиграет. В то же время нужно рассмотреть все возможные ответы Пети, чтобы доказать, что у него нет шансов на выигрыш при правильной игре Вани. В этом суть теории игр – добиться лучшего результата в худшем случае, то есть при безошибочной игре соперника.
Разбор проекта демонстрационной версии ЕГЭ-2018. Фишки
Два игрока, Петя и Ваня играют в следующую игру. На столе в кучке лежат фишки. На лицевой стороне каждой фишки написано двузначное натуральное число, обе цифры которого находятся в диапазоне от 1 до 4. Никакие две фишки не повторяются. Игра состоит в том, что игроки поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают. Верхняя часть всех выложенных фишек направлена в одну сторону, то есть переворачивать фишки нельзя. Например, из фишки, на которой написано 23, нельзя сделать фишку, на которой написано 32. Первый ход делает Петя, выкладывая на стол любую фишку из кучки. Игра заканчивается, когда в кучке нет ни одной фишки, которую можно добавить в цепочку. Тот, кто добавил в цепочку последнюю фишку, выигрывает, а его противник проигрывает. Будем называть партией любую допустимую правилами последовательность ходов игроков, приводящую к завершению игры. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит указать, какую фишку он должен выставить в любой ситуации, которая ему может встретиться при различной игре противника.
Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.
Выполните следующие три задания при исходном наборе фишек <12, 14, 21, 22, 24, 41, 42, 44>.
а) Приведите пример самой короткой партии, возможной при данном наборе фишек. Если таких партий несколько, достаточно привести одну.
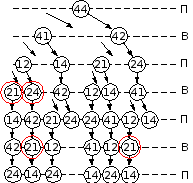
б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии.
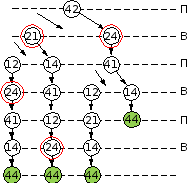
Пусть Петя первым ходом пошел 44. У кого из игроков есть выигрышная стратегия, позволяющая в этой ситуации выиграть своим четвертым ходом? Постройте в виде рисунка или таблицы дерево всех партий, возможных при реализации выигрывающим игроком этой стратегии. На рёбрах дерева указывайте ход, в узлах – цепочку фишек, получившуюся после этого хода.
Укажите хотя бы один способ убрать 2 фишки из исходного набора так, чтобы всегда выигрывал не тот игрок, который имеет выигрышную стратегию в задании 2. Приведите пример партии для набора из 6 оставшихся фишек.
партия заканчивается, когда цепочка закончилась на цифре X и не осталось ни одной фишки, которая бы начиналась с этой цифры;
меньше всего фишек заданного набора начинается с цифры 1 (только 12 и 14), поэтому самой короткой партией, вероятно, будет партия, которая заканчивается на цифре 1 (фишкой 21 или 41), при этом фишки 12 и 14 должны быть выставлены;
соединить эти фишки в цепочку можно с помощью фишек 21 или 41, таким образом, получается две возможных самых коротких партии:
12 – 21 – 14 – 41 и 14 – 41 – 12 – 21.
В ответе достаточно привести одну из них.
Задание 1б. (Идея решения – А. Сидоров).
заметим, что эта игра напоминает «одностороннее домино», в котором фишки можно выставлять только одной стороной и наращивать цепочку можно тоже только с одной стороны;
среди фишек есть две особые – 22 и 44 («дубли») они служат для того, чтобы передать ход сопернику; если выставить дубль, оказавшись в проигрышной позиции, то эта проигрышная позиция «переходит» к сопернику
пока построим дерево без учёта дублей, то есть для набора фишек
12, 14, 21, 24, 41 и 42
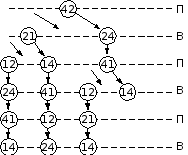
по условию Петя выставляет первым ходом фишку 42, дальнейшие варианты развития игры показаны на схеме:
итак, мы видим, что если никто из игроков не выставляет дублей, то выигрывает Ваня во всех случаях, причем все партии заканчиваются на цифре 4
если Ваня в ходе игры не выставит дубль, то в конце каждой ветки Петя может выставить дубль 44 и выиграть:
поэтому теперь посмотрим, где Ваня может изменить игру дублями; Ване нет смысла ставить дубль 44, потому что во всех вариантах партий он уже есть (с выигрышем для Пети), так что выставление дубля 44 просто перемещает его в середину цепочки, не изменяя её длину
у Вани в распоряжении есть еще дубль 22; на следующем рисунке выделены ходы, где Ваня может поставить этот дубль:
использование дубля 22 действительно изменяет игру, так как удлиняет цепочки на 1, при этом выигрывает Ваня:
а) Ваня может своим первым ходом выставить дубль 22, при этом он всегда выиграет
б) Ваня может первым ходом выставить фишку 21, при этом получив ход в позиции, когда текущая цепочка заканчивается на 2, он выставляет дубль 22 и выигрывает
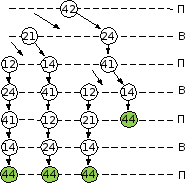
построим дерево игры для случая, когда Петя в самом начале ходит фишкой 44, «забыв» пока про дубль 22:
по дереву видим, что при игре без дубля 22 выигрывает Петя своим третьим или четвёртым ходом
Ваня может изменить ход игры дублем 22 только в выделенных узлах, поэтому
если Ваня походит фишкой 41, Петя должен ответить ходом 14
если Ваня походит фишкой 42, Петя должен ответить ходом 21
при записи неполного дерева игры, доказывающего выигрыш Пети, нужно учесть, что по условию задачи нужно представить дерево с выигрышем именно в 4 хода, хотя Петя имеет стратегию выигрыша за 3 хода:
в задании 2 выигрывает Петя, поэтому нужно убрать две фишки таким образом, чтобы всегда выигрывал Ваня
заметим, что нам нужно доказать, что Ваня выигрывает ВСЕГДА, при любом первом ходе Пети; это значит, что построение одного дерева (при конкретном первом ходе) ничего не доказывает
заметим, что последней цифрой цепочки для данного набора фишек всегда будет 1, 2 или 4, поэтому можно построить такой граф возможных переходов (например, ребро перехода 1 2 соответствует фишке 12, а петля у узла 2 – фишке 22):
по каждому ребру этого графа можно пройти только один раз (каждая фишка выставляется один раз)
по этому графу видно, что если убрать две петли, остается граф с одинаковой ситуацией для каждой из вершин: есть два контура, проходящие в разных направлениях через все узлы
итак, если убрать два дубля, то всегда будут выставлены 4 или все 6 фишек, поскольку 4 и 6 – чётные числа, то всегда выиграет Ваня, потому что он делает все ходы с чётными номерами; например, при первом ходе Пети 12 возможны партии:
– 21 – 14 – 41 или 12 – 24 – 41 – 14 – 42 – 21.
Разбор задачи основного периода ЕГЭ-2018. Две кучи
Задание №26 (2018 г, основной период)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 63. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 63 камня или больше.
В начальный момент в первой куче было пять камней, во второй куче – S камней; 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Выполните следующие задания.
а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход.
б) Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети.
Укажите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы).
В узлах дерева указывайте позиции, на рёбрах рекомендуется указывать ходы. Дерево не должно содержать партии, невозможные при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Если во второй куче было S камней, то после первого хода Пети количество камней в двух кучах может стать равным
6+S (после добавления 1 камня в любую кучу)
10+S (после удвоения первой кучи)
5+2S (после удвоения второй кучи)
Выписываем условия выигрыша на первом ходу для всех трёх вариантов
Отсюда следует, что при S 29 Петя выиграет первым же ходом, удвоив число камней во второй куче.
S=29. Если Петя сделал неудачный ход, значит он имел выигрышную стратегию, при которой необходимо было увеличить вторую кучу вдвое. Пусть он при этом положил в первую или во вторую кучу 1 камень и привел Ваню к выигрышу. Значит у Вани была позиция (5, 30) или (6, 29). Ваня удваивает вторую кучу и выигрывает, получив позицию (5, 60) или (6, 58).
В позиции (5,28) своим первым ходом Петя должен добавить 1 камень в первую кучу, приведя противника к проигрышной ситуации (6, 28). Вторым ходом Петя удваивает количество камней во второй куче и выигрывает.
Выигрышная стратегия – урок информатики. 3-й класс
Презентация к уроку
Тип урока – изучение нового материала.
Обучающие – формирование знаний по теме “выигрышная стратегия”; учиться находить закономерность в ходе игры, формулировать и применять выигрышную стратегию (“секрет выигрыша”).
Развивающие – развивать интерес к данной теме и к предмету информатика в целом; развивать логическое мышление; расширять кругозор учащихся.
Воспитательные – способствовать формированию познавательного интереса как компонента учебной мотивации; способствовать развитию учебной и творческой активности учащихся.
1. Приветствие. Проверка присутствия учащихся на уроке.
2. Тема нашего сегодняшнего урока “Выигрышная стратегия”. Приложение
Вы любите играть? А какие бывают игры? Чем отличаются и чем бывают похожи игры?
Люди придумали очень много разных игр: спортивных, настольных и т.д. Давайте поближе познакомимся с настольными играми. Эти игры можно разделить на два основных типа: игры, где всего два участника (соперника), например, нарды, и игры, в которых могут участвовать более двух игроков, например, лото.
Игры, в которых участвуют только два игрока тоже можно разделить на две группы. К первой группе относятся игры, где игроки делают ходы по очереди и обдумывают каждый ход, потому что он зависит от действий соперника (например, шашки, шахматы). Ко второй группе можно отнести игры, где ходы игроков никак не зависят от ходов противника (морской бой, игры с кубиком и фишками).
Итог обсуждения: (Слайд 2)
3. Знакомство с понятием “стратегия игры”. (Слайд 3).
В ряде задач задается один и тот же вопрос: кто из двух игроков выиграет при правильной игре? Всегда ли выигрывает тот игрок, который начинает игру (или имеет 2-ой ход)?
Слова «правильная игра» означают, что если у кого-то из игроков есть стратегия, позволяющая выигрывать при любых ходах другого игрока, и он не делает «глупых» ходов, а стремится выиграть и следует своей выигрышной стратегии.
В каждой задаче необходимо придумать такую стратегию для одного из игроков.
4. Игра “Кто первым назовет число 100”. (Слайд 4).
В игре “Кто первым назовет число 100” участвуют двое. Один называет любое число от 1 до 9 включительно. Другой прибавляет к названному числу любое число от 1 до 9 и называет сумму. К этой сумме первый снова добавляет любое число от 1 до 9 и называет новую сумму. Выигрывает тот, кто назовет число 100. Кто выиграет при правильной игре?
Учащиеся читают условие игры и двое играют. Остальные слушают, если необходимо, дополняют или поправляют играющих, разгадывая секрет выигрыша в данной игре. (Выигрывает второй игрок, дополняя ходы первого игрока до круглого числа – 10, 20, 30 и т.д.)
5. Понятие “Выигрышная стратегия”. (Слайды 5, 6).
Разбор игры “Не больше двух предметов”. Поиск секрета выигрыша.
Рабочая тетрадь “Информатика в играх и задачах” 3 класс, ч.2 №№ 34, 35 (1, 2).
6. Формулировка “секрета выигрышной стратегии”. (Слайд 7).
Правила (секреты) выигрышной стратегии
Правило 1. Перед началом игры раздели все предметы на группы ОТ КОНЦА К НАЧАЛУ. Кол-во предметов в группе определяется условиями (не больше 2, тогда группы по 3, т.е. (n+1)). Самая первая группа может оказаться неполной – эти предметы мы называем “лишними”.
Правило 2. Если есть “лишние” предметы, то выбери 1-ый ход и закрась “лишние” предметы. Если нет “лишних” предметов – то выбери второй ход.
Правило 3. Дополняй ход другого игрока до (n+1) предмета, тогда в последней группе самый последний предмет будет твой.
7. Итог урока
Итак, мы сегодня с вами познакомились с очень интересным понятием “выигрышная стратегия”, которая используется в простейших играх с участием двух игроков.
8. Домашнее задание: рабочая тетрадь “Информатика в играх и задачах” 3 класс, ч.2 №35 (3, 4).
Разбор задачи “Ступеньки” в двух вариантах:
Играют два карандаша – синий и желтый. Они по очереди закрашивают нарисованные ступеньки. За один ход можно закрасить одну или две ступеньки. Выигрывает тот, кто закрасит последнюю ступеньку. (Можно вызвать более слабых учеников, чтобы убедиться в усвоении материала).
Играют два карандаша – синий и желтый. Они по очереди закрашивают нарисованные ступеньки. За один ход можно закрасить одну, две или три ступеньки. Выигрывает тот, кто закрасит последнюю ступеньку.
Что изменилось в данной игре по сравнению с предыдущими заданиями про бусины и кольца пирамидки? Один из учеников разбирает этот вариант задачи (№ 36 по тетради).
4. Разбор дополнительных задач. (Слайды 9, 10).
Задача № 1. У ромашки вариант А) 12 лепестков; вариант Б) 11 лепестков.
За ход каждому игроку (всего их двое) разрешается сорвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает игрок, который не сможет сделать ход. Кто выигрывает при “правильной” игре? Какой ход он должен выбрать? Как должен ходить?
Задача № 2. Имеются 2 кучи камней. Двое играющих берут по очереди камни. Разрешается взять один камень из любой кучи или по одному камню из обеих куч. Выигрывает взявший последние камни. При каком числе камней в кучах выиграет начинающий?
Эти задачи на самом деле аналогичны задаче “Не больше двух”.
5. Разбор шахматных задач. (Слайды 11, 12).
Выигрышная стратегия используется в разных задачах. Например, есть несколько задач на шахматной доске, в которых тоже необходимо отыскать выигрышную стратегию.
1 вариант: Король стоит на поле a1. Играют двое. За ход разрешается сдвинуть короля на одну клетку вправо или на одну клетку вверх. Выигрывает тот, кто поставит короля на поле h8. Кто из игроков обладает выигрышной стратегией?
2 вариант: Ладья стоит на поле a1. Играют двое. За ход разрешается сдвинуть ладью на любое число клеток вправо или на любое число клеток вверх. Выигрывает тот, кто поставит ладью на поле h8. Кто из игроков обладает выигрышной стратегией?
Задача 2*. Двое играют на шахматной доске, передвигая по очереди одного короля. Допускаются ходы на одно поле влево, вниз или влево-вниз по диагонали. Выигрывает тот, кому удастся поставить короля на левый нижний угол.
При каких начальных положениях короля выигрывает начинающий, а при каких – его соперник?
Данная задача более сложная, так как надо определить начальные условия, но для сильных учеников может быть очень интересна.
6. Задача для любознательных (слайд 13).
Эта задача была предложена на Международной математической олимпиаде школьников в 2008 году.
Задача. Двое играющих по очереди (пропускать ход нельзя) выставляют на стол либо одну фишку, либо столько, сколько их уже стоит на столе, если нужное число фишек еще осталось в коробочке. Выигрывает тот, кто ставит последнюю фишку. В начале игры на столе фишек нет, а в коробочке: а) 5 фишек; б) 6 фишек; в) 7 фишек; г) 8 фишек.
Кто выиграет, если будет играть наилучшим способом? Как должен “ходить” победитель?
7. Повторение материала уроков. Подведение итогов. (Слайд 14).
8. Домашнее задание: рабочая тетрадь “Информатика в играх и задачах” 3 кл., ч.2 № 37.