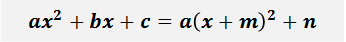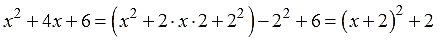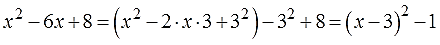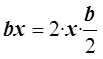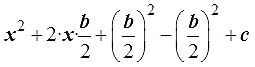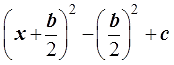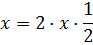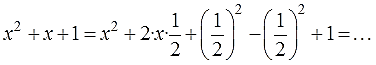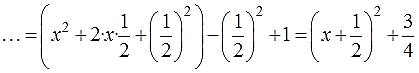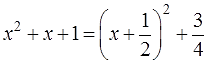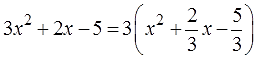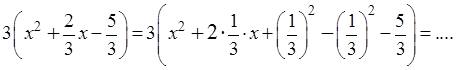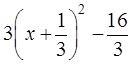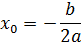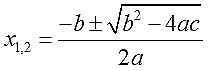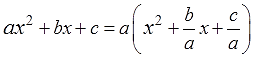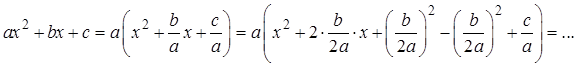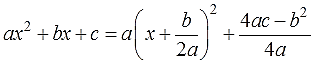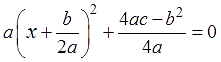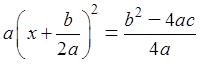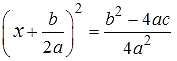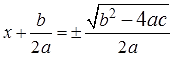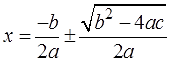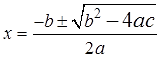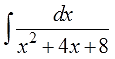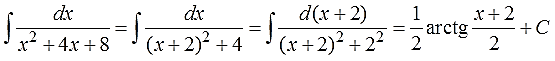Что такое выделить полный квадрат
Что такое выделить полный квадрат
Описание метода выделения полного квадрата
§2. Выделение полного квадрата из квадратного трёхчлена
Описание метода выделения полного квадрата
Преобразование, которое мы сделали, носит название «выделение полного квадрата из квадратного трёхчлена».
Прибавим и вычтем к полученному выражению `(1/2)^2`, получаем
Покажем, как применяется метод выделения полного квадрата из квадратного трёхчлена для разложения квадратного трёхчлена на множители.
Выделяем полный квадрат из квадратного трёхчлена:
Применяем формулу для разности квадратов, имеем:
Мы не можем представить выражение 3 x 2 как квадрат какого-то выражения, т. к. ещё не изучали этого в школе. Это будете проходить позже, и уже в Задании №4 будем изучать квадратные корни. Покажем, как можно разложить на множители заданный квадратный трёхчлен:
`(x)^2-2*x*1/2+(1/2)^2-(1/2)^2+3=(x-1/2)^2+11/4`. Заметим, что при `x=1/2` значение квадратного трёхчлена равно `11/4`, а при `x!=1/2` к значению `11/4` добавляется положительное число, поэтому получаем число, большее `11/4`. Таким образом, наименьшее значение квадратного трёхчлена равно `11/4` и оно получается при `x=1/2`.
Разложите на множители числитель и знаменатель дроби `
Применим к этому многочлену метод выделения полного квадрата.
Применяем метод выделения полного квадрата. Имеем:
Применяя метод выделения полного квадрата, разложите на множители числитель и знаменатель и сократите дробь `<8x^2+10x-3>/<2x^2-x-6>`.
Алгебра. 7 класс
Конспект урока
Выделение полного квадрата
Перечень рассматриваемых вопросов:
и уметь увидеть их в выражении.
Теоретический материал для самостоятельного изучения.
Вы познакомились с формулами сокращённого умножения и научились раскладывать по ним квадрат разности и квадрат суммы. На этом уроке вы узнаете, как выделить из многочлена полный квадрат.
Этот многочлен можно преобразовать следующим образом.
6а мы представим в виде удвоенного произведения двух множителей: 3 и a:
Далее применим формулу квадрата суммы для двучлена а +3.
Таким образом, получили равенство:
Представим 10у как удвоенное произведение 5 и у:
Применим формулу квадрата разности для двучлена
Выделение полного квадрата используется, например, при доказательстве неравенств или определения знака выражения. Например:
Доказать, что для любых чисел а и в верно неравенство
В левой части неравенства две переменных, поэтому разделим одночлены на две группы. Число 45 можно добавить в любую группу, например, в группу, где переменная b.
Сложим два полученных выражения. В результате получим сумму двух квадратов двучленов:
то и сумма этих выражений будет положительной либо равна нулю. Что и требовалось доказать.
Материал для углублённого изучения темы.
При выделении полного квадрата числа могут получаться не только целыми, но и дробными.
Разбор заданий тренировочного модуля.
Объяснение: число 6 не является квадратом целого числа, поэтому удобнее вынести его за скобку:
2. Представьте выражение в виде суммы квадратов:
Объяснение: разделим выражение на две группы. Число 50 можем присоединить к любой группе, например к группе, где переменная m.
Получим сумму квадрата двучлена m + 5 и числа 25:
Во второй группе представим 10n как удвоенное произведение 5 и n, прибавим и вычтем 25:
Однако не все его знают. В результате этого объем вычислений увеличивается, а также допускаются ошибки. Он также применяется для нахождения корней уравнений и построения графиков.
Общая информация
Выделить полный квадрат из многочлена второй степени означает, что его следует привести к более читабельной формуле. Эта операция применяется в следующих случаях: интегрирование, дифференцирование, построение графиков и решение уравнений (чаще — в последних двух).
За основу взяты три формулы сокращенного умножения (разложение квадратного многочлена на множители), которые специалисты рекомендуют запомнить или выписать отдельно.
К ним относятся следующие соотношения:
Существует правило, позволяющее выполнить операцию упрощения многочлена ay 2 + by + c второй степени путем разложения его на множители. Это означает, что его следует свести (преобразовать) к виду a * (y — y0)^2 + y0.
Универсальный алгоритм
Алгоритмом называется комплексное решение, состоящее из последовательного набора правил. Преобразование ay 2 + by + c осуществляется следующим образом:
Для квадрата разности алгоритм похожий. Формула выделения полного квадрата имеет такой вид: [(a)^(½) * y]^2 — [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c. Соотношение также применяется математиками в алгебре, а также в различных дисциплинах с физико-математическим уклоном. Для этого нужно воспользоваться таким подробным объяснением правил решения:
Число «а» может быть положительным или отрицательным. Если его прибавить к «с», то должно получиться значение «с1».
При извлечении квадратного корня результат должен быть целым. Чтобы равенство не нарушалось, следует прибавить и отнять «а».
Алгоритм записан в общем виде. В теории он является сложным для понимания.
Однако при практическом применении некоторые неясности исчезают. Для начала нужно разобрать, где его нужно применять.
Сферы использования
Математики рекомендуют разобрать основные примеры выделения полного квадрата. Следует их систематизировать, поскольку это позволит оптимизировать процесс решения. Основной смысл заключается в применении соответствующих алгоритмов для экономии времени.
Некоторые считают, что шаблонами пользоваться нежелательно. Однако в этом есть и свои положительные стороны. Например, при поступлении в какое-либо высшее учебное заведение следует придерживаться общепринятых вариантов решения. При успешном зачислении в университет можно применить нестандартные подходы выполнения задания.
Шаблоны широко применяются не только в дисциплинах с физико-математическим уклоном, но и в программировании.
Распространенными заданиями с упрощением квадратного трехчлена являются:
Для нахождения решений следует подробно разобрать алгоритмы. Нет необходимости заучивать основные определения, формулы и правила. Их следует понимать, поскольку в философии есть такой закон: «переход количества в качество». Кроме того, программистами были созданы специальные онлайн-калькуляторы, позволяющие получить полный квадрат, разложить многочлен на множители и так далее.
Построение графиков
Графиком квадратичной функции z = a[y — c]^2 + d является кривая, которая называется параболой. Далее следует ввести следующие пояснения:
Следует отметить, что расположение графика функции зависит от вышеописанных коэффициентов. Для построения параболы математики рекомендуют разобрать частные случаи:
При использовании первого метода нужно воспользоваться таким алгоритмом:
Когда коэффициент с = 0 (az 2 + bz = 0), то решить уравнение очень просто.
Для этого нужно произвести такие действия:
Третий способ — выделение квадрата или использование формул сокращенного умножения. В этом случае нет необходимости использовать стандартный первый метод. Если построить график функции, то корнями будут являться его точки пересечения с осью абсцисс. Можно получить решения при помощи математических преобразований. Последний считается менее точным способом, поскольку корнями могут быть иррациональные числа, а не действительные.
Упрощение выражений
Бывают случаи, когда следует решить уравнение, упростив его. Например, чтобы решить равенство (2z 2 — 5z + 7) + (z + 5)(z + 3) = 0, нужно раскрыть скобки, а затем привести подобные слагаемые. Этот способ называется методом математических преобразований.
В некоторых случаях следует возвести в квадрат, а затем привести подобные слагаемые. После этого необходимо опять воспользоваться формулами, сгруппировав элементы.
Этот шаг позволяет оптимизировать процесс вычислений. Например, нет необходимости подставлять численные значения в выражение z 2 + 4z + 16 + z 2 — 16. Его можно просто упростить: z 2 + 8z + 16 + z 2 — 16 = (z + 4)^2 + (z — 4)(z + 4) = (z + 4)(z + 4 + z — 4) = 2z (z + 4).
Пример решения
Необходимо решить квадратное уравнение z^2 + 20z + 50 = 6z + 5 несколькими способами, используя следующие методы: нахождение дискриминанта, формул разложения, теоремы Виета и построить график. Вычисление корней первым методом (через дискриминант) выглядит таким образом:
Два корня подходят, поскольку равенство 0 = 0 соблюдается. Специалисты рекомендуют опускать проверку, поскольку задача решается несколькими способами.
Третий метод заключается в использовании формул разложения. Их разрешается применять несколько раз и в любом порядке. Алгоритм решения выглядит таким образом:
Метод выделения полного квадрата
Итак, традиционно корни многочлена находят, разложив его на множители. Разложение на множители очень помогает в поиске корней, так как, если произведение равно нулю, то один из множителей равен 0. При разложении на множители помогает вынесение общего множителя за скобку (пожалуй, это первое, что следует делать при разложении на множители). Далее обычно происходит группировка (если нет общего множителя, или этого не достаточно). Это по аналогии можно назвать методом группировки: одночлены разделяются по группам, имеющим общий множитель. Далее в идеале появляется общий множитель у всего выражения, который можно вынести и продолжить разложение. Потом, используя формулы сокращённого умножения, можно закончить разложение.
Однако, есть ещё один приём, заслуживающий отдельного внимания, основанный на формулах квадрата суммы и разности. Метод выделения полного квадрата. Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Если найти что-то, отдалённо напоминающее квадрат суммы или разности, но без какой-то необходимой части, то её можно прибавить, а затем отнять, тем самым не меняя конечного значения выражения. Далее, свернув квадрат суммы/разности, обычно нужно применить ещё какую-то формулу (например, разности квадратов) или совершить какую-то последовательность действий, и многочлен разложится на множители.
Также метод выделения полного квадрата позволяет именно решать квадратные уравнения. Для этого есть хорошо определённый и вполне известный алгоритм (написан для a x ²+b x +c = 0).
У многих квадратных уравнений есть более красивые и простые решения.
Формула корней полного квадратного уравнения
Начнём, как водится, с записи квадратного уравнения общего вида: a x ²+b x +c = 0. А затем, можно проделать над уравнением ряд действий, основанных на алгоритме.
Соответственно при решении квадратных уравнений по формуле целесообразно поступать по данному алгоритму.
Выделение полного квадрата двучлена из квадратного трёхчлена
Умение проделывать такую процедуру крайне необходимо во многих темах математики, связанных с квадратным трёхчленом ax 2 +bx+c. Самые распространённые:
2) Решение многих заданий на квадратный трёхчлен (квадратные уравнения и неравенства, задачи с параметрами и т.д.);
3) Работа с интегралами от некоторых функций, содержащих квадратный трёхчлен, а также работа с кривыми второго порядка (для студентов).
Полезная штука, короче! Претендуете на пятёрку? Тогда осваиваем!)
Что значит выделить полный квадрат двучлена в квадратном трёхчлене?
Это задание означает, что исходный квадратный трёхчлен c помощью тождественных преобразований выражений надо преобразовать вот к такому виду:
Число a что слева, что справа — одно и то же. Коэффициент при квадрате икса. Потому и обозначен одной буквой. Умножается справа на квадрат скобок. В самих скобках сидит тот самый двучлен, о котором и идёт речь в этой теме. Сумма чистого икса и какого-то числа m. Да, прошу обратить внимание, именно чистого икса! Это важно.
А вот буковки m и n справа — некоторые новые числа. Какие уж получатся в результате наших преобразований. Они могут получиться положительными, отрицательными, целыми, дробными — всякими! В примерах ниже сами увидите. Эти числа зависят от коэффициентов a, b и c. Для них есть свои специальные общие формулы. Достаточно громоздкие, с дробями. Поэтому давать их прямо здесь и сейчас я не буду. Зачем вашим светлым головам лишний мусор? Да и неинтересно это. Поработаем творчески.)
Что необходимо знать и понимать?
Прежде всего, необходимо знать назубок формулы сокращённого умножения. Хотя бы две из них — квадрат суммы и квадрат разности.
Без этой парочки формул — никуда. Не только в этом уроке, а почти во всей остальной математике вообще. Намёк понятен?)
Но одних лишь механически заученных формул здесь недостаточно. Нужно ещё грамотно уметь применять эти формулы. Причём не столько напрямую, слева направо, сколько наоборот, справа налево. Т.е. по исходному квадратному трёхчлену уметь расшифровывать квадрат суммы/разности. Это значит, вы должны легко, на автомате, узнавать равенства типа:
Без этого полезного навыка — тоже никак… Так что если с этими простыми вещами проблемы, то закрывайте эту страницу. Рановато вам сюда.) Сначала сходите по ссылочке выше. Она — для вас!
Ах, вы давно в теме? Отлично! Тогда читаем дальше.)
Как выделить полный квадрат двучлена в квадратном трёхчлене?
Начнём, разумеется, с простого.
Уровень 1. Коэффициент при x 2 равен 1
Это самая простая ситуация, требующая минимум дополнительных преобразований.
Например, дан квадратный трёхчлен:
Внешне выражение очень похоже на квадрат суммы. Мы знаем, что в квадрате суммы сидят чистые квадраты первого и второго выражений (a 2 и b 2 ), а также удвоенное произведение 2ab этих самых выражений.
Почти всё. Остаётся лишь добавить 6, в соответствии с исходным трёхчленом. Шестёрка-то никуда не делась! Пишем:
Скобки сути выражения не меняют, зато чётко подсказывают, что, как и почему. Осталось свернуть эти три слагаемых в полный квадрат по формуле, сосчитать в числах оставшийся хвостик -2 2 +6 (это будет 2) и записать:
Всё. Мы выделили квадрат скобок (x+2) 2 из исходного квадратного трёхчлена х 2 +4х+6. Превратили его в сумму полного квадрата двучлена (x+2) 2 и некоторого постоянного числа (двойки). А теперь я запишу всю цепочку наших преобразований в компактном виде. Для наглядности.
И все дела.) Вот и вся суть процедуры выделения полного квадрата.
Кстати, чему здесь равны числа m и n? Да. Каждое из них равно по двойке: m=2, n=2. Так уж получилось в ходе выделения.
Выделить полный квадрат двучлена:
И опять первый взгляд — на слагаемое с иксом. Превращаем 6х в удвоенное произведение икса и тройки. Перед удвоенным — минус. Значит, выделяем квадрат разности. Прибавляем (для получения полного квадрата) и тут же вычитаем (для компенсации) тройку в квадрате, т.е. 9. Ну и про восьмёрку не забываем. Получим:
Улавливаете принцип? Тогда настал черёд освоить и общий алгоритм. Всё то же самое, но через буквы. Итак, перед нами квадратный трёхчлен x 2 +bx+c (a=1). Что мы делаем:
1. Смотрим на слагаемое с иксом в первой степени ( bx) и превращаем его в удвоенное произведение икса на b/2:
2. К удвоенному произведению прибавляем и тут же отнимаем квадрат числа b/2. Прибавляем — для дополнения до полного квадрата. Отнимаем — для компенсации. В самом конце прибавляем свободный член с.
3. Первые три слагаемых сворачиваем в квадрат суммы/разности по соответствующей формуле. Оставшееся снаружи выражение аккуратно считаем в числах.
Ясненько? Первые два примера были совсем простые, с целыми числами. Для знакомства. Хуже, когда в процессе преобразований вылезают дроби. Главное здесь — не бояться! А чтобы не бояться, всяко надо знать действия с дробями, да…) Но здесь же пятёрочный уровень, не так ли? Усложняем задачу.
Допустим задан такой трёхчлен:
Как в этом трёхчлене организовать квадрат суммы? Не вопрос! Точно так же. Работаем по пунктам.
1. Смотрим на слагаемое с иксом в первой степени ( bx) и превращаем его в удвоенное произведение икса на b/2.
Наше слагаемое с иксом есть просто икс. И… что? Как нам одинокий икс превратить в удвоенное произведение? Да очень просто! Прямо по инструкции. Вот так:
Число b в исходном трёхчлене — единичка. Стало быть, b/2 получается дробным. Одна вторая. 1/2. Ну и ладно. Не маленькие уже.)
2. К удвоенному произведению прибавляем и тут же отнимаем квадрат числа b/2. Прибавляем — для дополнения до полного квадрата. Отнимаем — для компенсации. В самом конце прибавляем свободный член с.
3. Первые три слагаемых сворачиваем в квадрат суммы/разности по соответствующей формуле. Оставшееся снаружи выражение аккуратно считаем в числах.
Здесь m=1/2, а n=3/4. Дробные числа. Бывает. Такой уж трёхчлен попался…
Такая вот технология. Разобрались? Можно двигать на следующий уровень?)
Уровень 2. Коэффициент при x 2 не равен 1 — как быть?
Это более общий случай по сравнению со случаем а=1. Объём вычислений, разумеется, возрастает. Это огорчает, да… Зато общий ход решения в целом остаётся прежним. Просто к нему добавляется всего один новый шаг. Это радует.)
Пока рассмотрим безобидный случай, безо всяких дробей и прочих подводных камней. Например:
В серединке стоит минус. Значит, будем подгонять под квадрат разности. Но коэффициент при квадрате икса — двойка. А проще работать с единичкой. C чистым иксом. Что делать? А вынесем-ка эту двойку за скобки! Чтоб не мешала. Имеем право! Получим:
Вот так. Теперь трёхчлен в скобках — уже с чистым иксом в квадрате! Как того требует алгоритм уровня 1. И теперь уже можно работать с этим новым трёхчленом по старой отработанной схеме. Вот и действуем. Выпишем-ка его отдельно да преобразуем:
Полдела сделано. Осталось вставить полученное выражение внутрь скобок, да раскрыть их обратно. Получится:
Фиксируем в голове:
Если коэффициент при квадрате икса не равен единице, то выносим этот коэффициент за скобки. С оставшимся внутри скобок трёхчленом работаем по привычному алгоритму для a=1. Выделив в нём полный квадрат, вставляем результат на место, а внешние скобки раскрываем обратно.
А если коэффициенты b и с не делятся нацело на а? Это — самый общий и одновременно самый скверный случай. Тогда только дроби, да… Ничего не поделать. Например:
Всё аналогично, отправляем тройку за скобки, получаем:
К сожалению, ни двойка, ни пятёрка нацело на тройку не делятся, поэтому коэффициенты нового (приведённого) трёхчлена — дробные. Ну и ничего страшного. Работаем прямо с дробями: две трети икс превращаем в удвоенное произведение икса на одну треть, прибавляем квадрат одной трети (т.е. 1/9), отнимаем его, отнимаем 5/3…
Дорешайте, чего уж там. Должно в итоге получиться:
И ещё одни грабли. Многие ученики лихо расправляются с положительными целыми и даже дробными коэффициентами, но зависают на отрицательных. Например:
Итого, с учётом минуса:
Вот и всё. Что? Не знаете, как выносить минус за скобки? Ну, это вопрос к элементарной алгебре седьмого класса, не к квадратным трёхчленам…
Зачем нужно уметь выделять полный квадрат?
Например, такое задание:
Что делать будем? По точкам строить? Можно, конечно. Маленькими шажочками по длинной дороге. Довольно тупо и неинтересно…
Прежде всего, напоминаю, что при построении любой параболы мы всегда предъявляем ей стандартный набор вопросов. Их два. А именно:
1) Куда направлены ветви параболы?
2) В какой точке находится вершина?
С направлением ветвей всё ясно прямо из исходного выражения. Ветви будут направлены вниз, ибо коэффициент перед x 2 — отрицательный. Минус один. Минус перед квадратом икса всегда переворачивает параболу.
А вот с расположением вершины всё не так очевидно. Есть, конечно, общая формула вычисления её абсциссы через коэффициенты a и b.
Но далеко не каждый помнит эту формулку, ох не каждый… А 50% тех, кто всё-таки помнит, спотыкаются на ровном месте и косячат в банальной арифметике (обычно при подсчёте игрека). Обидно, правда?)
Сейчас вы научитесь искать координаты вершины любой параболы в уме за одну минуту! И икс и игрек. Одним махом и безо всяких формул. Как? С помощью выделения полного квадрата!
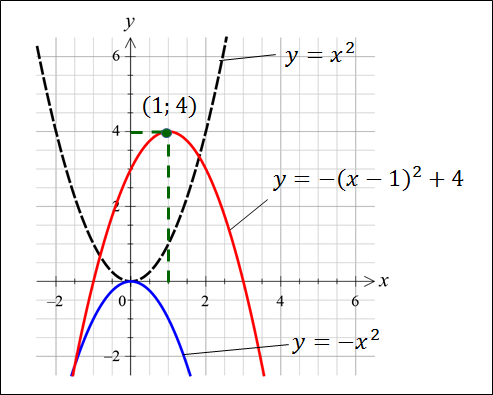
Итак, выделим полный квадрат в нашем выражении. Получим:
Кто хорошо прошарен в общих сведениях о функциях и хорошо освоил тему «преобразования графиков функций», тот без труда сообразит, что наша искомая парабола получается из обычной параболы y=x 2 c помощью трёх преобразований. Это:
1) Смена направления ветвей.
2) Параллельный перенос параболы у=- x 2 по иксу на 1 единицу ВПРАВО.
3) Параллельный перенос параболы y=-( x-1) 2 по игреку на 4 единицы ВВЕРХ.
Картинка будет следующей:
Собственно, именно по этой причине я с такой настойчивостью заострял ваше внимание на числах m и n, получающихся в процессе выделения полного квадрата. Не догадались, зачем? Да. Дело в том, что точка с координатами (-m; n) — это всегда вершина параболы y=a(x+m) 2 +n. Просто смотрим на числа в преобразованном трёхчлене и в уме даём верный ответ, где находится вершина. Удобно, правда?)
Рисование парабол — это первая полезная вещь. Переходим ко второй.
Полезная вещь вторая — решение квадратных уравнений и неравенств.
Да-да! Выделение полного квадрата во многих случаях оказывается гораздо быстрее и эффективнее традиционных приёмов решения подобных заданий. Сомневаетесь? Пожалуйста! Вот вам задание:
Узнали? Да! Это классическое квадратное неравенство. Все такие неравенства решаются по стандартному алгоритму. Для этого нам надо:
1) Сделать из неравенства уравнение стандартного вида и решить его, найти корни.
2) Нарисовать ось Х и отметить точками корни уравнения.
3) Схематично изобразить параболу по исходному выражению.
4) Определить области +/- на рисунке. Выбрать нужные области по исходному неравенству и записать ответ.
Собственно, весь этот процесс и напрягает, да…) И, более того, не всегда спасает от ошибок в нестандартных ситуациях типа этого примера. Попробуем сначала по шаблону?
Итак, выполняем пункт первый. Делаем из неравенства уравнение:
Стандартное квадратное уравнение, без фокусов. Решаем! Считаем дискриминант:
Вот-те раз! А дискриминант-то отрицательный! Нет корней у уравнения! И на оси рисовать нечего… Что делать?
Вот тут некоторые могут сделать вывод, что исходное неравенство тоже не имеет решений. Это фатальное заблуждение, да… Зато с помощью выделения полного квадрата верный ответ к этому неравенству можно дать за полминуты! Сомневаетесь? Что ж, можете засекать время.
Итак, выделяем полный квадрат в нашем выражении. Получаем:
Исходное неравенство стало выглядеть вот так:
А теперь, ничего далее не решая и не преобразовывая, просто включаем элементарную логику и соображаем: если к квадрату какого-то выражения (величине заведомо неотрицательной!) прибавить ещё единичку, то какое число мы в итоге получим? Да! Строго положительное!
А теперь смотрим на неравенство:
Переводим запись с математического языка на русский: при каких икс строго положительное выражение будет строго больше нуля? Не догадались? Да! При любых!
Вот вам и ответ: х — любое число.
А сейчас вернёмся к алгоритму. Всё-таки понимание сути и простое механическое заучивание — вещи разные.)
Суть алгоритма в том, что мы из левой части стандартного неравенства делаем параболу, и смотрим, где она выше оси Х, а где ниже. Т.е. где положительные значения левой части, где отрицательные.
Если мы сделаем из нашей левой части параболу:
и нарисуем её график, то увидим, что вся парабола целиком проходит выше оси Х. Картинка будет выглядеть вот так:
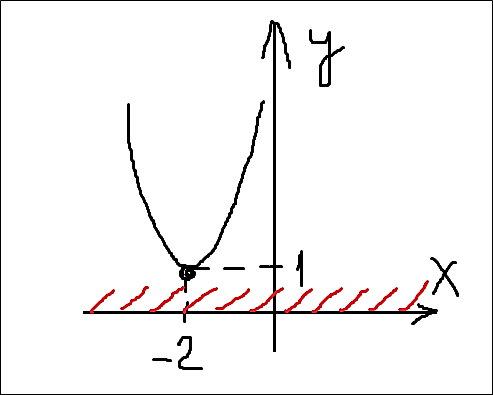
Парабола кривовата, да… На то она и схематичная. Но при этом всё что нам надо, на картинке видно. Нет у параболы точек пересечения с осью Х, нет нулевых значений игрека. И отрицательных значений, естественно, тоже нет. Что и показано штриховкой всей оси Х целиком. Кстати, ось Y и координаты вершины я здесь изобразил не зря. Сравните координаты вершины параболы (-2; 1) и наше преобразованное выражение!
И как вам? Да! В нашем случае m=2 и n=1. Стало быть, вершина параболы имеет координаты: (-m; n) = (-2; 1). Всё логично.)
Простецкое квадратное уравнение. Можно решать по старинке, через дискриминант. Можно через теорему Виета. Как угодно. Математика не возражает.)
А если ни тот, ни другой способы того… не помним? Что ж, двойка вам светит, по-хорошему, но… Так уж и быть, спасу! Покажу, как можно решать некоторые квадратные уравнения только лишь методами седьмого класса. Снова выделяем полный квадрат!)
А теперь расписываем полученное выражение как… разность квадратов! Да-да, есть такая формула сокращённого умножения в седьмом классе:
Вставляем это разложение в уравнение вместо квадратного трёхчлена:
Осталось сообразить, что произведение множителей равно нулю тогда и только тогда, когда какой-нибудь из них равен нулю. Вот и приравниваем (в уме!) к нулю каждую скобку.
Вот и всё. Те же самые два корня. Такой вот искусный приёмчик. В дополнение к дискриминанту.)
К слову, о дискриминанте и об общей формуле корней квадратного уравнения:
Полезная вещь третья — вывод формулы корней квадратного уравнения.
Ну что, поехали! Берём квадратный трёхчлен в общем виде ax 2 +bx+c и… начинаем выделять полный квадрат! Да, прямо через буквы! Была арифметика, стала — алгебра.) Сначала, как обычно, выносим букву a за скобки, а все остальные коэффициенты делим на a:
Вот так. Это вполне законное преобразование: а не равно нулю, и делить на неё можно. А со скобками снова работаем по обычному алгоритму: из слагаемого с иксом делаем удвоенное произведение, прибавляем/отнимаем квадрат второго числа…
Всё то же самое, но с буквами.) Попробуйте доделать сами! Полезно!)
После всех преобразований у вас должно получиться вот что:
И зачем нам из безобидного трёхчлена сооружать такие нагромождения — спросите вы? Ничего, сейчас интересно будет! А теперь, знамо дело, приравниваем эту штуку к нулю:
Решаем как обычное уравнение, работаем по всем правилам, только с буквами. Делаем элементарные тождественные преобразования уравнений:
2) Очищаем квадрат скобок от коэффициента. Делим обе части на «а«. Слева, перед скобками, буква а исчезает, а справа уходит в знаменатель большой дроби, превращая его в 4a 2 .
Получается вот такое равенство:
У вас не так вышло? Тогда тема «Как выразить переменную из формулы?» — для вас. Срочно туда!
Следующим шагом извлекаем корень. Нас же икс интересует, верно? А икс под квадратом сидит… Извлекаем по правилам извлечения корней, разумеется. После извлечения получится вот это:
Слева квадрат суммы исчезает и остаётся просто сама эта сумма. Что и требуется.) А вот справа появляется плюс/минус. Ибо наша здоровенная дробь, несмотря на её устрашающий вид, это просто какое-то число. Дробное число. Зависящее от коэффициентов a, b, c. При этом корень из числителя этой дроби красиво не извлекается, там разность двух выражений. А вот корень из знаменателя 4a 2 вполне себе извлекается! Получится просто 2a.
Подумайте, почему знак модуля я всё-таки опустил. Очень полезно. Подсказка: ответ кроется в знаке плюс/минус перед дробью.)
Остались сущие пустяки. Обеспечиваем слева чистый икс. Для этого маленькую дробь переносим вправо. Со сменой знака, ясен перец. Напоминаю, что знак в дроби можно менять где угодно и как угодно. Хотим перед дробью поменяем, хотим в знаменателе, хотим в числителе. Я поменяю знак в числителе. Было +b, стало –b. Надеюсь, возражений нет?) После переноса станет так:
Складываем две дроби с одинаковыми знаменателями и получаем (наконец-то!):
Ну? Что тут сказать? Вау!)
Полезная вещь четвёртая — студентам на заметку!
А теперь плавненько переместимся из школы в ВУЗ. Вы не поверите, но выделение полного квадрата в высшей математике тоже нужно!
Например, такое задание:
Найти неопределённый интеграл:
С чего начинать? Прямое применение таблицы интегралов не катит. Только выделение полного квадрата и спасает, да…)
Кто не умеет выделять полный квадрат, тот навсегда зависнет на этом несложном примере. А кто умеет, тот выделяет и получает:
И теперь интеграл (для знающих) берётся одной левой!
Здорово, правда? И это не только интегралы! Я уж молчу про аналитическую геометрию, с её кривыми второго порядка — эллипсом, гиперболой, параболой и окружностью.
Определить тип кривой, заданной уравнением:
Без умения выделять полный квадрат задание не решить, да… А ведь пример проще некуда! Для тех, кто в теме, разумеется.
Группируем в кучки члены с иксом и с игреком и выделяем полные квадраты по каждой переменной. Получится:
Ну и как? Узнали, что за зверь?) Ну, конечно! Окружность радиуса тройка с центром в точке (3; 4).
И все дела.) Полезная штука — выделение полного квадрата!)