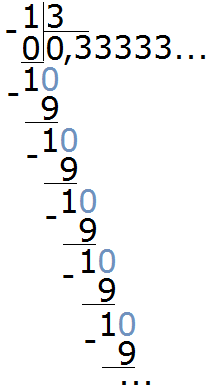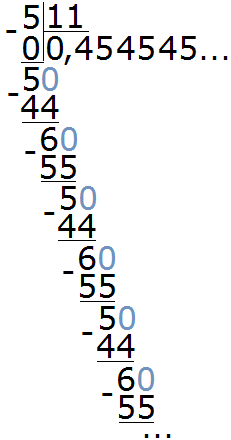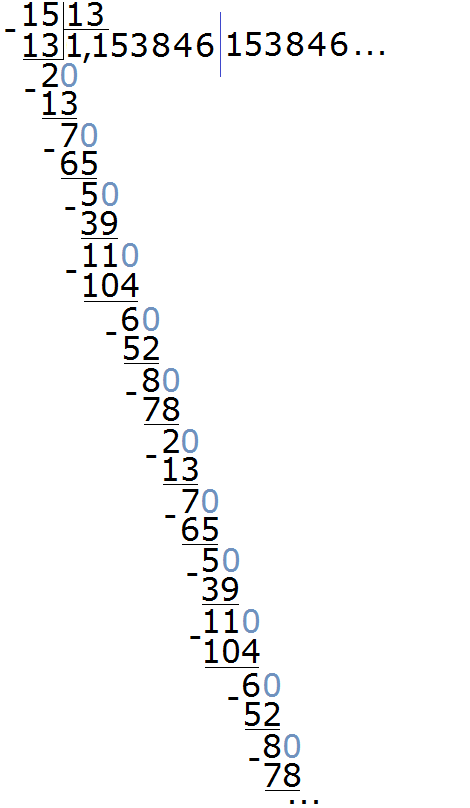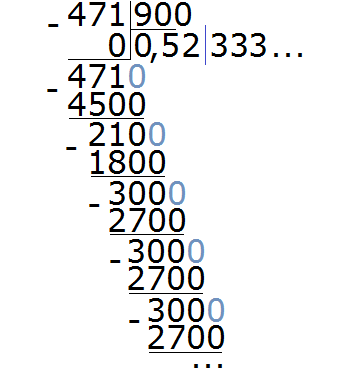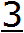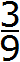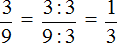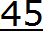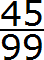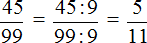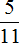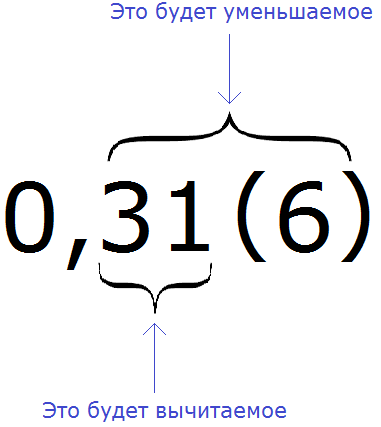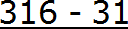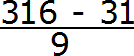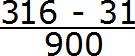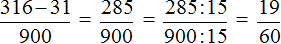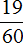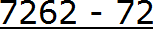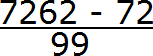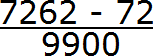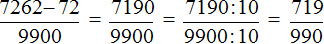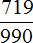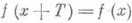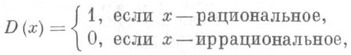Что такое второй период в математике
Как определить периодичность функции
Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
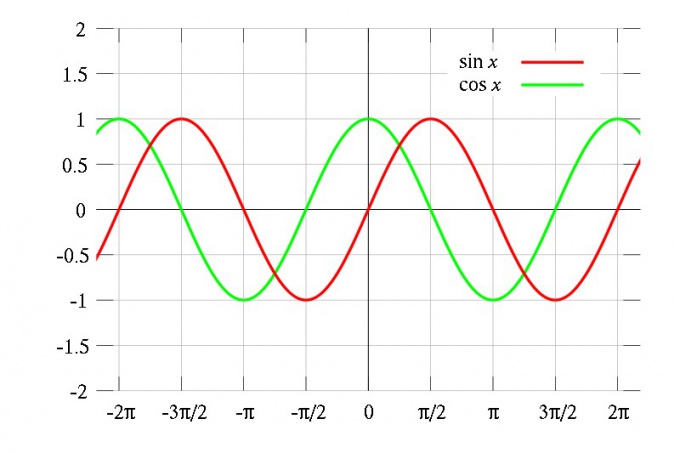
Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Периодические дроби
Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:
Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.
Получаем периодическую дробь
Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.
Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.
Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.
В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:
Читается как «ноль целых и три в периоде»
Пример 2. Разделить 5 на 11
Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:
Читается как «ноль целых и сорок пять в периоде»
Пример 3. Разделить 15 на 13
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».
Пример 4. Разделить 471 на 900
В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:
Читается как: «ноль целых пятьдесят две сотых и три в периоде».
Виды периодических дробей
Периодические дроби бывают двух видов: чистые и смéшанные.
Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:
Видно, что в этих дробях период начинается сразу после запятой.
Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:
Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.
Избавляемся от хвоста
Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.
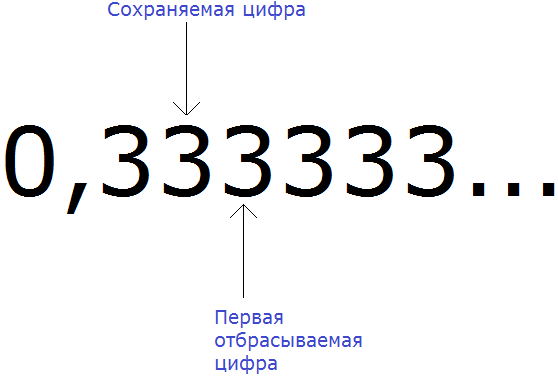
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33
Округлим периодическую дробь 6,31 (6) до разряда тысячных.
Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317
Перевод чистой периодической дроби в обыкновенную дробь
Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.
Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.
Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.
В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.
Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.
Итак, записываем в числителе период дроби 0, (3) то есть тройку:
А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).
В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:
Полученную дробь 
Получили обыкновенную дробь 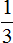
Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается
Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.
Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:
А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).
В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:
Полученную дробь 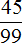
Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается
Перевод смешанной периодической дроби в обыкновенную дробь
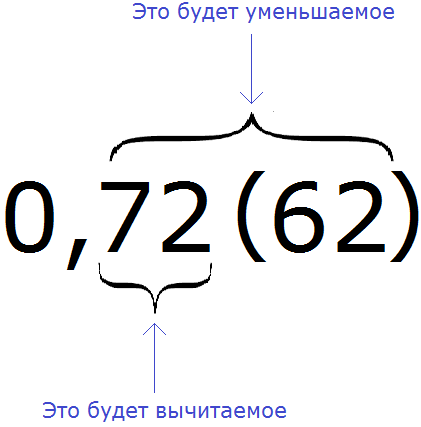
Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)
В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь
Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:
Итак, записываем в числителе разность:
А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)
В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:
Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.
В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:
Получили выражение, которое вычисляется легко:
Получили ответ
Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
34 thoughts on “Периодические дроби”
Когда же следующие уроки? Уже что-то долго ничего нету
Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)
Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.
Спасибо большое Тэла, за столь добрый отзыв 😉
Если люди получают пользу от этих уроков — это уже отдача)
Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)
Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?
Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…
Спасибо большое за урок 🙂 Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?
Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?
зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых
ПЕРИОД
любое рациональное число 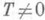
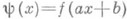
Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков.
Полезное
Смотреть что такое «ПЕРИОД» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
период
Его стихи, романы и автобиографические книги повествуют о разных периодах его карьеры искателя приключений, авиатора, журналиста и поэта.
О минувших периодах истории мы судим по сохранившимся до наших дней памятникам культуры.
Период вращения этого спутника вокруг оси равен периоду его обращения вокруг Земли.
Полезное
Смотреть что такое «период» в других словарях:
Период — (греч. periodos «обход», «окружность») термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или… … Литературная энциклопедия
ПЕРИОД — периода, м. [греч. periodos] (книжн.). 1. Промежуток времени, в течение к–рого заканчивается какой–н. повторяющийся процесс (науч.). Синодический период обращения планеты (время, в течение к–рого планета совершает один полный оборот вокруг… … Толковый словарь Ушакова
Период — ПЕРИОД (Περιοδος обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состязания во время олимпийских празднеств. Этим термином Аристотель стал обозначать особый вид… … Словарь литературных терминов
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
ПЕРИОД — муж. срок или промежуток времени, продолжительность; время от одного события до другого. История делится на периоды, сроки. Период первозданный период осадочный, сроки образованья земной толщи. | Длительность самого события, действия, состоянья;… … Толковый словарь Даля
ПЕРИОД — (1) промежуток времени, в течение которого начинается, развивается и заканчивается какой либо процесс; наименьший интервал времени, по истечении которого произвольно выбранные мгновенные значения периодической величины повторяются; (2) П. в… … Большая политехническая энциклопедия
Период С — Студийный а … Википедия
ПЕРИОД — срок протекания экономического процесса, действия, плана, договора, гарантии, уплаты долгов, внесения налогов, выполнения работ (гарантийный период, плановый период, период обложения, период окупаемости). Райзберг Б.А., Лозовский Л.Ш.,… … Экономический словарь
период — См … Словарь синонимов
ПЕРИОД — колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие период… … Современная энциклопедия
Что такое математика? Девять в периоде
Не секрет, что детьми лучше всего запоминается тот материал, который вызвал в их головах разрыв старых шаблонов и категорический отказ от принятия новых фактов. Но самое приятное в таких ситуациях, на наш взгляд, то, что вы чувствуете себя немножко Эйнштейном, раздвигающим горизонты сознания, но, в отличие от последнего, заставляющим (наконец-то!) вам не верить.
Выпуску 2013 от всего сердца
В конце концов, окружность бесконечно
большого круга и прямая линия — одно и то же.
Галилео Галилей
Слово «период» вызывает вполне определенную ассоциацию в головах у граждан, утомленных суровой окружающей действительностью. А именно — «время». То есть они, эти граждане, на вопрос «С чем ассоциируется слово “период”», как заведенные твердят: «время». Рассчитывать на фантазию, в общем-то, не приходится.
Как же заставить работать обленившееся в связи с ускоряющимся прогрессом правое полушарие? И тут спешит на помощь великая и ужасная МАТЕМАТИКА! Да-да, слово напускает страху на неокрепшую психику не менее живо, нежели сама математичка с треугольником в руке.
Но необходимо отметить, что именно эта почтенная дама (или уважаемый джентльмен) в свое время отчаянно пыталась обогатить ваш словарный запас, объясняя, что словом «период» можно назвать не только промежуток времени, но и «бесконечно повторяющуюся группу цифр» после запятой в записи десятичной дроби. И такие дроби называются периодическими.
Изнуренные средним образованием граждане, скорее всего, ведают, что любую обыкновенную дробь можно записать в виде десятичной — конечной или бесконечной. При этом в последнем случае и происходит чудесное явление периода.
Например, если долго делить «столбиком» два на три, то получится следующее:
2/3 = 2 : 3 = 0,666… = 0,(6).
Обратный процесс не менее увлекателен. Если возникает непреодолимое желание перевести периодическую дробь в обыкновенную, то стоит предпринять такие действия:
Поклон. Аплодисменты. Занавес. Все в восторге собираются расходиться. И тут — ехидный голос училки:
— А переведите мне, дорогие мои детишечки, 0,(9) в обыкновенную дробь.
Да проще пареной репы! По образцу работать — антресоли заполнять не надо:
пусть x = 0,(9), тогда 10x = 9,(9). Вычтем из второго уравнения первое:
10x – x = 9,(9) – 0,(9), то есть 9x = 9. Откуда x = 1. Значит, 0,(9) = 1.
В этом месте, как правило, возникает когнитивный диссонанс в головах отроков, доселе уныло взирающих на доску. Потому как среди прочего они видят:
0,(9) = 1.
Кто-то тоскливо подумал о том, что он так и знал, что учителям верить нельзя. Кто-то заплакал и выбежал. Некоторые счастливцы не слушали, поэтому сохранили свой мозг в девственной чистоте и продолжают пребывать в неведении относительно разразившейся катастрофы в головах коллег.
И тут голос, как из преисподней:
— Не верите мне? АХАХАХАХАХ А я вам сейчас с помощью суммы бесконечно убывающей геометрической прогрессии докажу.
И на доске возникает примерно следующее:
Как страшно жить! Если учитель при этом вздумал упомянуть о том, что можно доказать это равенство, используя понятие предела, то он — садист. Если еще проскользнуло что-то вроде «а это — бесконечно малое», то, вообще, монстр.
Оставляя российскому образованию радость разбираться с мучителями детей, необходимо сделать вывод относительно вышеописанных результатов.
Если в вашей обычной повседневной жизни вам потребуется выполнить какую-нибудь интересную, но, скорее всего, странную работу, поскольку вы будете манипулировать с 0,(9), то помните, что это — 1.
Всем — спасибо! Все свободны!
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
Кстати, такая возможность есть
на всех страницах нашего сайта