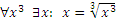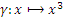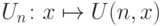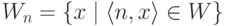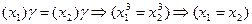Что такое всюду определенная функция
Универсальные функции и неразрешимость
Универсальные функции
Говорят, что функция U двух натуральных аргументов является универсальной для класса вычислимых функций одного аргумента, если для каждого n функция
Аналогичное определение можно дать и для других классов функций (одного аргумента): например, функция U двух аргументов будет универсальной для класса всех всюду определенных вычислимых функций одного аргумента, если ее сечения Un являются всюду определенными вычислимыми функциями одного аргумента и исчерпывают все такие функции. Очевидно, универсальные функции существуют для любых счетных классов (и только для них).
Ключевую роль в этом разделе играет такой факт:
Теорема 6.Существует вычислимая функция двух аргументов, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.
15. Все сечения Un некоторой функции U двух аргументов вычислимы. Следует ли отсюда, что функция U вычислима?
16. Дайте (естественное) определение понятия вычислимой функции трех аргументов, универсальной для класса вычислимых функций двух аргументов, и докажите ее существование.
Для множеств используется аналогичная терминология: множество 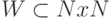
множества W принадлежат этому классу и других множеств в классе нет.
Теорема 7.Существует перечислимое множество пар натуральных чисел, универсальное для класса всех перечислимых множеств натуральных чисел.
18. Существует ли разрешимое множество пар натуральных чисел, универсальное для класса всех разрешимых множеств натуральных чисел?
Диагональная конструкция
В предыдущем разделе мы построили универсальную функцию для класса всех вычислимых функций одного аргумента. Можно ли сделать то же самое для класса всюду определенных вычислимых функций? Оказывается, что нет.
Теорема 8.Не существует вычислимой всюду определенной функции двух аргументов, универсальной для класса всех вычислимых всюду определенных функций одного аргумента.
Тем не менее, часть рассуждения остается в силе.
19. Докажите, что и сама функция d из доказательства предыдущей теоремы не имеет вычислимого всюду определенного продолжения.
04. Функция
Пусть Х и У два множества и F отношение в Х´У.
Определение. Отношение F называется Функцией из Х в У, если оно удовлетворяет свойству:
Из xFy и xFz следует, что y = z.
Из приведенных примеров 1 и 3 определяют функцию, а 2 и 4 не являются функцией, т. к. не выполнено определение функции.
Для функции применяются также другие названия: преобразование, отображение, соответствие. Если y = F(x), то x называют Аргументом функции, а y Образом.
Две функции F и G считаются равными, если выполнены равенства соответствующих множеств. Последнее эквивалентно следующим двум равенствам:
DF =DG и F(x)=G(x) для «xÎDF.
Следующие определения переносятся с отношений:
1) В случае, когда DF = Х функцию называют Всюду определенной.
2) Функция F из Х в У называется Сюръекцией (или Отображением на), если RF =У.
3) Функция F из Х в У называется Инъекцией (Или однозначным отображением), если из х1 ¹ х2 следует, что F(х1) ¹ F(х2).
Всюду определенная функция F из Х в У называется Биекцией, если она одновременно является сюръекцией и инъекцией.
Определение. Для функции F из Х в У функция G из У в Х называется Правой обратной (соответственно, Левой обратной), если справедливо равенство FoG=IУ (соответственно, GoF=IХ), где через IХ (IУ) обозначено тождественное отображение на Х (соответственно на У), т. е. IХ(x) = x (IУ(y) = y).
Лемма 1. Если функция F имеет левую обратную, то F является инъекцией.
Лемма 2. Если функция F имеет правую обратную, то F является сюръекцией.
Доказательство. Утверждение легко вытекает из определения правой обратной функции G: для любого уÎУ Þ FoG(у)=у.
Лемма 3. Если у функции F из Х в У существуют левая и правая обратная функции, то они совпадают.
Теорема. Пусть F является функцией из Х в У. Для существования обратной функции F-1 из У в Х необходимо и достаточно, чтобы F была биекцией.
Необходимость легко вытекает из лемм 1 и 2.
Достаточность. Пусть yÎУ. Так как F является сюръекцией, то существует хÎХ такое, что F(x)=y. При этом такое х одно, так как F также и инъекция. Определим функцию G(x)=y. Легко проверить, что таким образом определенная функция является обратной к F.
Следствие. Если F является биекцией, то и F-1 также является биекцией.
1. Установить, что следующие отношения являются функцией:
А) вÎУ, R = X´<в>ÍX´У (постоянное отображение);
Б) R = <(x, x): xÎX>ÍX´X (тождественное отображение IX);
В) R = <((x, y), x)>Í(X´Y)´X ( проекция на Х);
Г) R = <((x, y), у)>Í(X´Y)´Y ( проекция на Y).
4. Верны ли равенства:
11. Задана функция f из А в В. Доказать, что следующие условия попарно эквивалентны:
В) f(ЕÇМ) = f(Е)Çf(М) для любых Е, МÍА;
Г) f(Е)Çf(М) = Æ для любой пары множеств ЕÍА, МÍА такой, что ЕÇМ= Æ;
Д) F(Е – М) = f(Е) – f(М) для любой пары множеств ЕÍА, МÍА такой, что МÍЕ.
12. Пусть даны множества А, В, С, D и функции
F: А ® В, g: В ® С, h: С ® D.
Доказать, что если каждая из суперпозиций gof и hog есть биекция, то и все функции f, g и h являются биекциями.
А) если f является сюръекцией, то f также и инъекция;
В) если f является инъекцией, то f также и сюръекция.
14. Построить отношения, удовлетворяющие следующим требованиям:
А) рефлексивное, симметричное, не транзитивное;
Б) рефлексивное, транзитивное, не симметричное;
В) симметричное, транзитивное, не рефлексивное.
Главные универсальные функции и множества



Определение 6.2.1. Универсальная функция U двух натуральных аргументов называется главной универсальной функцией, если для любой вычислимой функции V существует всюду определенная вычислимая функция s(m), для которой V(m, x)=U(s(m), x) при всех m и x (значения V и U либообане определены, либо определены и равны).
Теорема 6.2.1. Существует главная универсальная функция.
Доказательство. Зафиксируем некоторое взаимнооднозначное соответствие 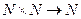
Пусть далее R(x,y) – вычислимая универсальная функция для вычислимых функций одной переменной. Положим T(n, u, v)= R(n, [u, v]).
Если V(u, v) – произвольная вычислимая функция двух аргументов, то функция f([u, v])=V(u, v) – вычислимая функция одного аргумента, и поскольку R(x,y) – универсальна, то найдется число n, для которого R(n, x)=f(x) длялюбых x. Для этого n выполнены равенства
Определим U([n, u], v)=T(n, u, v). Тогда согласно предыдущим рассуждениям для произвольной вычислимой функции двух аргументов V(u, v) можнонайти число n, для которого V(u, v)=T(n, u, v)=U([n, u], v) длявсех u и v. Полагая s(u)=[n,u], имеем V(u, v)=U(s(u), v)).
Теорема 6.2.2. Пусть U(u, v) – главная универсальная функция для класса вычислимых функций одного аргумента. Тогда существует всюду определенная функция c(p, q) такая, что U(c(p, q), x)=U(p, U(q, x)) для всех p, q и x.
Доказательство. Положим V([p, q], x)=U(p, U(q, x)). По определению главной универсальной функции найдется такая всюду определенная вычислимая функция одного аргумента s(m), что V(m, x)=U(s(m), x)) для всех m и x.
Тогда функция c(p, q)= s([p, q]) будет искомой.
Теорема 6.2.3. Пусть U(u, v) – универсальная функция для класса вычислимых функций одного аргумента. Если существует всюду определенная функция c(p, q) такая, что U(c(p, q), x)=U(p, U(q, x)) для всех p, q и x, тофункция U(u, v) являетсяглавной универсальной функцией.
Определение 6.2.2. Перечислимое множество 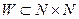
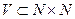
Теорема 6.2.3. Существует главное универсальное перечислимое множество 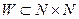
Доказательство. Пусть U(u, v) – главная универсальная функция для класса вычислимых функций одного аргумента, W – ее областьопределения. Пусть далее 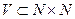
Таким образом, можно утверждать, что область определения главной универсальной функции для класса вычислимых функций одного аргумента является главным универсальным перечислимым множеством для класса перечислимых подмножеств N.
Теорема 6.2.4. Пусть 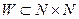
Для доказательства теоремы необходимо определить множество 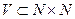
Нумерации и операции
Главные универсальные функции
Очевидно, композиция двух вычислимых функций вычислима. При этом это утверждение кажется «эффективным» в том смысле, что по программам двух функций можно алгоритмически получить программу их композиции. В разумном языке программирования она будет состоять из двух подпрограмм, соответствующих двум вычислимым функциям, и главной программы с единственной строкой » return (f(g(x))) «.
Однако мы хотим говорить не о программах (чтобы не вдаваться в детали языка программирования), а о номерах функций. Для этого у нас есть средства. Именно, всякая универсальная функция U для класса вычислимых функций одного аргумента задает нумерацию этого класса: число n является номером функции 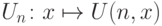
при всех m и x ( равенство понимается, как обычно, в том смысле, что либо оба значения не определены, либо определены и равны).
(Второй способ.) Но можно и не вдаваться в детали построения универсальной функции, а воспользоваться лишь фактом ее существования.
Нумерации, соответствующие главным универсальным функциям, называют главными, или геделевыми.
Теперь уже можно доказать точный вариант утверждения, с которого мы начали.
Любопытно, что верно и обратное к теореме 16 утверждение:
Естественный вопрос: существуют ли вычислимые универсальные функции, не являющиеся главными? Мы увидим дальше, что существуют.
29. Изменим определение главной универсальной функции и будем требовать существования » транслятора» s лишь для универсальных вычислимых функций V (а не для любых, как раньше). Покажите, что новое определение эквивалентно старому. (Указание: любую функцию можно искусственно переделать в универсальную, » растворив» в ней любую другую универсальную функцию.)
Свойства и типы соответствий



Виды соответствий
Соответствие 
а) 
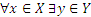
б) 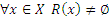
в) из каждого элемента множества X выходит стрелка и приходит в Y.
Соответствие 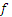
а) 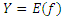
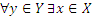
б) 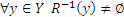
в) в каждый элемент множества Y приходит стрелка из X.
Соответствие f называют функциональным, если:
а) 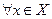
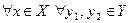
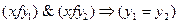
б) на языке графов это означает, что из каждого элемента множества X не выходит две стрелки и более.
а) 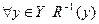
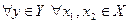
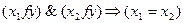
б) на «языке» графов это означает, что в каждый элемент множества Y приходит не более одной стрелки.
П р и м е р 1: Соответствие на рисунке
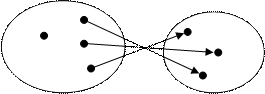 |
а) не всюду определено;
Это соответствие будет:
 |
а) всюду определенным, если каждый студент будет сидеть;
б) сюрьективным, если все стулья заняты;
в) функциональным, если каждый студент не сидит на двух стульях;
г) инъективным, если на каждом стуле не сидят два студента.
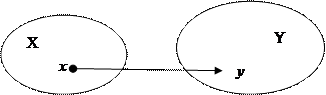
П р и м е р 3: Пусть х f у 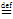
 |
Соответствие это будет:
а) всюду определено, так как 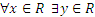
б) функционально, так как 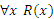
г) не сюръективно, так как 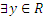
Рассмотренные выше свойства соответствий (инъективность, сюръективностъ и т.п.) позволяют классифицировать все соответствия на определенные типы. Приведем классификацию соответствий по свойствам в виде таблицы:
| Функциональность | Всюду определенность | Инъективность | Сюръективность | Название |
| + | Функция типа 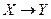 | |||
| + | + | Отображение из X в Y | ||
| + | + | + | Вложение(инъекция) X в Y | |
| + | + | + | Наложение (сюръекция) X на Y | |
| + | + | + | + | Биекция X на Y |
П р и м е р 4: Отображение 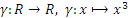
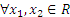
и