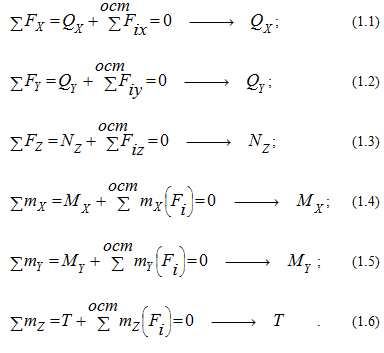Что такое всф в сопромате

Сопромат online

Расчеты в режиме online

1.3. Метод сечений. Внутренние силовые факторы.

Целостность твердого тела, его форма обусловливаются на­личием сил взаимодействия между его частицами. При дефор­мации тела под действием внешних нагрузок и других внеш­них воздействий происходит изменение сил взаимодействия между частицами тела. Эти изменения сил взаимодействия в сопротивлении материалов называются внутренними силами. Таким образом, под внутренними силами необходимо пони­мать силы взаимодействия между частицами тела, возника­ющие только в результате деформации тела. При отсутствии де­формации внутренние силы в теле считаются равными нулю.

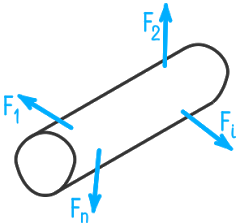
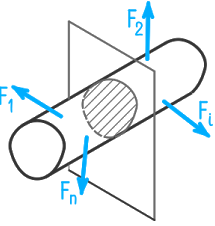
Для определения внутренних сил необходимо, используя метод сечений, перевести их в категорию сил внешних. На рисунке 1 представлено твердое тело, на которое действует про­извольная система внешних сил F₁, F₂….F_n, удовлетворя­ющая условиям равновесия. Мысленно рассечем тело плоскостью на две части и отбросим одну часть.

Рисунок 1.2 Произвольная система сил.

Чтобы любая часть, например левая, находилась в равнове­сии, необходимо действие отброшенной правой части на рас­сматриваемую левую заменить в сечении внутренними силами. В другом сечении они будут другими. Внутренние силы всегда взаимны: правая часть действует на левую так же, как левая на правую. Внутренние силы считаются поверхностными, т.е. принимается, что взаимодействие частиц, примыкающих с раз­ных сторон к сечению, является контактным и что частицы, расположенные за сечением, во взаимодействии не участвуют.

Метод сечений — это прием, позволяющий обнаруживать внутренние силы и рассматривать их как внешние силы по от­ношению к оставшейся (рассматриваемой) части тела.

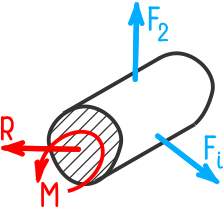
Приведем систему внутренних сил, используя положения статики, к центру тяжести сечения (рисунок 1.3 а).

Рисунок 1.3.а Внутренние силы, приведенные к центру тяжести сечения.

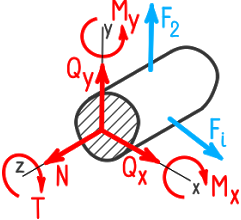
В результате приведения получим главный вектор Fc и главный момент Мс, разложив которые по осям координат, получим три силы и три момента Fх, Fу, Fz, Мх, Му, Мz (рисунок 1.3 б).

Рисунок 1.3.б Внутренние силовые факторы.

Эти составляющие обозначаются специальными буквами и на­зываются внутренними силовыми факторами. F_x = N- назы­вается продольной или нормальной силой; F_z =Q_Z и F_y=Q_y назы­ваются поперечными силами; М_х = Т называется крутящим мо­ментом; М_у и M_z называются изгибающими моментами относи­тельно осей у и z.

Для отсеченной части в общем случае можно составить шесть уравнений равновесия :

Согласно (1.8) нормальная сила N в поперечном сечении равна алгебраической сумме проекций на ось x всех внешних сил, действующих на отсеченную часть тела; поперечные силы Q_y и Q_z в сечении — соответственно равны алгебраической сумме проекций на оси у и z, расположенные в рассматриваемом се­чении, всех внешних сил, действующих на отсеченную часть тела; крутящий момент Т в поперечном сечении равен алгебра­ической сумме моментов относительно оси х всех внешних сил, действующих на отсеченную часть тела; изгибающие мо­менты М_у и М_z в сечении соответственно равны алгебраиче­ской сумме моментов относительно осей у и z рассматриваемо­го сечения всех внешних сил, действующих на отсеченную часть тела. Результаты будут одинаковыми независимо от того, какая отсеченная часть тела рассматривается.

Таким образом, в расчетных схемах как внешние нагрузки, так и внутренние силовые факторы нужно рассматривать как скалярные величины.

Нормальная сила, направленная от сечения, вызывает в се­чении растяжение материала и считается положительной, а на­правленная к сечению — вызывает в сечении сжатие материала и считается отрицательной.

Поперечная сила считается положительной, если внешние силы стремятся вращать отсеченную часть тела (бруса или ра­мы) относительно проведенного сечения по часовой стрелке; если — против часовой стрелки, то поперечная сила считается отрицательной.

Крутящий момент в сечении считается положительным, ес­ли при взгляде на сечение со стороны внешней нормали внеш­ние силы стремятся вращать отсеченную часть по часовой стрелке, если — против часовой стрелки, то крутящий момент в сечении считается отрицательным.

Изгибающий момент от внешних сил, вызывающих сжатие верхних волокон балки или сжатие наружных волокон рамы, считается положительным, а от внешних сил, вызывающих сжа­тие нижних волокон балки или внутренних волокон рамы, — от­рицательным.

Нагружение называется простым, если в поперечных сече­ниях элемента конструкции возникает только один внутрен­ний силовой фактор, или сложным (комбинированным), если в поперечных сечениях элемента одновременно действуют не­сколько внутренних силовых факторов.

Внутренние силовые факторы вдоль элемента (бруса) изме­няются. Эпюрами называются графики, показывающие, как из­меняются внутренние силовые факторы в сечениях по длине бруса (балки). (Пример построения эпюр ступенчатого стержня)

Эпюры позволяют установить положение опасного сече­ния, в котором действуют максимальные внутренние силы и моменты.

Источник

Что такое всф в сопромате

Составители: А.С. Савинов, Журавлев В.В., Яременко В.Н.

Определение внутренних силовых факторов в стержнях, балках и рамах: Метод. указ. по дисциплине “Сопротивление материалов” для студентов всех специальностей. Магнитогорск: ГОУ ВПО МГТУ, 2008. 39 с.

Рассмотрен метод установления взаимосвязи внутренних силовых факторов с внешними. Разработаны оригинальные расчетные схемы с целью изучения напряженного состояния стержней балок и рам при деформациях кручения, растяжения-сжатия, изгиба

Рецензент Д.В. Терентьев

ВВЕДЕНИЕ

Внутренние силы (силы упругости), возникающие в теле под действием нагрузки, — силы непрерывно распределенные (в соответствии с принятым допущением о непрерывности материала тела).

Как определяются эти силы в любой точке тела, будет показано ниже.

Теперь же займемся определением тех равнодействующих уси лий (в том числе и моментов), к которым приводятся в сечении эти силы упругости. Эти равнодействующие усилия представляют собой не что иное, как составляющие главного вектора и главного момента внутренних сил.

Для определения внутренних усилий (или внутренних силовых фак торов) применяется метод сечений (правило РОЗУ), заключающийся в следующем.

Для тела, находящегося в равно весии (рис. 1), в интересующем нас месте мысленно делается разрез, например по а — а.

После этого составляют уравнения равновесия для отсеченной части тела, из которых и определяются N , Q , М. Действительно, проецируя силы, действующие на отсеченную часть, на направле ние оси стержня и приравнивая сумму проекций нулю, найдем N ;

проецируя силы на направление, перпендикулярное оси стержня, определим Q ; приравнивая нулю сумму моментов относительно какой-либо точки, определим М.

Итак, для нахождения внутренних усилий необходимо:

1) разрезать стержень или систему стержней;

2) отбросить одну часть;

4) найти значения усилий «из уравнений равновесия, составленных для отсеченной части.

В частном случае в поперечном сечении стержня могут возникать:

1. Только продольная сила N. Этот случай нагружения назы вается растяжением (если сила N направлена от сечения) или сжатием (если продольная сила направлена к сечению).

2. Только поперечная сила Q_x или Q_y . Это случай сдвига.

4. Только изгибающий момент М_х или М_у. Это случай изгиба.

Если число неизвестных усилий равно числу уравнений рав новесия, задача называется статически определимой, если же число неизвестных усилий больше числа уравнений равновесия — статически неопределимой.

Для статически неопределимых задач кроме уравнений равнове сия необходимо использовать еще дополнительные уравнения при рассмотрении деформации системы.

Источник

Внутренние силовые факторы — справочник

Привет! Этот справочник, на портале – SoproMats, будет по внутренним силовым факторам при различных видах деформаций: растяжении и сжатии, кручении и изгибе. По каждому фактору будет написана специальная статья, где расскажем, как обозначается, в чем измеряется и как рассчитывается. Для подробного изучения каждого силового фактора, перемещайтесь по указанным гиперссылкам.

ВСФ при растяжении и сжатии

Как известно, при растяжении и сжатии (центральном) возникает один единственный внутренний силовой фактор – продольная сила. В указанной статье рассказывается, что это за сила, в чем измеряется и т.д.

Если вкратце рассказывать, то продольная сила рассчитывается методом сечений, который предполагает, что если вся конструкций находится в равновесии, то и отдельные ее части также будут находится в равновесии, если действие частей друг на друга заменить силовыми факторами.

ВСФ при кручении

При кручении, также как при растяжении и сжатие, в поперечных сечениях действует один силовой фактор – крутящий момент. В статье рассказывается об данном факторе, как он рассчитывается, в каких расчетах используется и как обозначается.

ВСФ при поперечном изгибе

При поперечном изгибе, чаще всего, в сечениях возникают два силовых фактора – поперечная сила и изгибающий момент. Поперечная сила, как правило, используется в проверочном расчете на прочность по касательным напряжениям, а также служит вспомогательным инструментов для определения экстремумов на эпюре изгибающих моментов.

Изгибающий момент используется при проведения прочностных расчетов по нормальным напряжениям. Подробнее об данных величинах можете узнать, перейдя по указанным ссылочкам.

Источник

iSopromat.ru

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

По своей природе внутренние силовые факторы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций. Для определения этих усилий применяют метод сечений:

надо мысленно рассечь брус, находящийся в равновесии, на две части

и рассмотреть равновесие одной из них.

Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой R и внутренним моментом M.

Для упрощения расчетов силу R и момент M принято раскладывать на составляющие усилия относительно осей координат x, y и z.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части (уравнения статики):

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Правила знаков для внутренних силовых факторов

Для определения знаков внутренних усилий, возникающих в брусе при различных способах его нагружения, приняты следующие правила:

Эпюры внутренних силовых факторов

В инженерной практике особое место занимает умение ясно представить взаимодействие усилий в конструкции, а также связь между внешними и внутренними силами в элементах конструкции, для этого графически изображают внутренние силовые факторы в функции осевой координаты и называют эти графики — эпюрами.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Техническая механика

Сопротивление материалов

Построение эпюр в сопромате

Прикладное значение науки сопротивление материалов заключается в возможности определения основных критериев работоспособности деталей машин и различных конструкций – прочности, деформации и устойчивости.
Применяя метод сечений в сочетании с приемами статики и других разделов прикладной механики, можно определить напряжения, возникающие в том или ином сечении бруса (детали, элемента конструкции), и, исходя из анализа полученного результата, сделать выводы о работоспособности этого бруса при приложении к нему расчетных нагрузок.
Именно напряжение является основным фактором, влияющим на прочностные характеристики элемента конструкции, а также его способность противостоять деформации. По этой причине в сопромате главной задачей, чаще всего, является определение напряжений, возникающих в том или ином сечении детали или элемента конструкции.

Для удобства анализа напряженности отдельных участков и сечений конструкции (бруса) используют графическое изображение нагрузок и напряжений в каждом сечении. Это позволяет визуально анализировать распределение нагрузок и напряжений по всей длине бруса, определять при этом наиболее нагруженные (критические) участки и сечения. Такие графические изображения нагрузок, напряжений, а также деформаций элементов конструкций называют эпюрами.

При анализе степени напряженности и деформирования элемента конструкции (детали, бруса) наиболее часто производят построение следующих типов эпюр:

Иногда на одной эпюре показываются несколько внутренних силовых факторов (эпюра продольных и поперечных сил, эпюра изгибающего и вращающего моментов), но такие эпюры при сложных нагрузках и переменных сечениях бруса сложны для чтения.

Как упоминалось выше, наиболее важную информацию о прочностных характеристиках элемента конструкции (бруса), т. е. способности противостоять разрушению, можно получить, используя эпюры напряжений, а информацию о степени деформации под действием расчетной нагрузки – по эпюрам перемещений.
Эпюры внутренних усилий и моментов в большинстве случаев не дают полной информации о степени напряженности и деформирования отдельных сечений и участков бруса, а являются промежуточным звеном при построении эпюр напряжений и перемещений, особенно если брус имеет ступенчатую форму или переменное поперечное сечение по длине.

Правила построения эпюр

При построении эпюр придерживаются определенных стандартных правил, позволяющих одинаково читать, истолковывать и анализировать эпюру всем участникам процесса конструирования изделия.

Построение эпюры начинают с изображения нулевой линии, которая символизирует линию бруса в ненапряженном состоянии. При этом, если брус имеет сложную пространственную форму, нулевая линия эпюры повторяет контуры центральной (осевой) линии бруса, и имеет такую же пространственную форму.

Нулевую линию эпюры обозначают названием и нулевым символом. Слева от нулевой линии указывается название эпюры (эпюра сил, моментов, напряжений и т. п.), справа от нулевой линии ставится цифра « 0 ». При указании называния эпюры обычно используют символ изображаемой нагрузки, например, внутренние продольные силы чаще всего обозначаются буквой « N », поперечные – буквой « Q », эпюры изгибающих моментов – буквами « M_из », эпюры вращающих моментов – буквами « Т » или « M_кр », эпюры напряжений – буквами « σ » или « τ » и т. п. Рядом с буквенным названием эпюры (или под ним) указывается единица измерения (ньютон, мегапаскаль, мм и т. п.).

Следующий этап построения эпюры – определение границ силовых участков бруса, т. е. таких участков, где внутренний силовой фактор в сечениях или деформация бруса изменяются по одной закономерности (или остаются постоянными). Как правило, границами силовых участков являются сечения, где приложена внешняя нагрузка или (и) площадь поперечного сечения бруса изменяется. В некоторых случаях, при построении эпюр брусьев сложной объемной формы, границы участков определяют аналитически. Границы силовых участков обозначаются тонкими вертикальными линиями, проведенными от изображения бруса через все эпюры.

Для оптимальной наглядности графика эпюры важно правильно выбрать масштаб изображаемого силового фактора, напряжения или деформации. Если масштаб окажется слишком мелким – эпюра будет трудна для чтения и анализа, если слишком крупным – она займет много места на чертеже.
Если учесть, что для одного бруса выполняют, как правило, несколько эпюр, расположенных одна под другой, то крупный масштаб не позволит выполнить построение эпюр на одном листе.
Для правильного выбора масштаба эпюры предварительно следует просчитать значение отображаемого фактора по всем контрольным сечениям бруса, и после этого определиться с масштабом.
Если, например, в результате расчетов окажется, что вся эпюра займет положительную область (над нулевой линией), то при построении графика эпюры это следует учесть.

Положительные значения фактора откладываются вверх от нулевой линии, отрицательные – вниз. Если на каком-либо участке силовой фактор равен нулю, эпюра совпадает с нулевой линией по всей длине этого участка. После построение внешнего контура эпюры на контрольных сечениях проставляются значения фактора (обычно на внешних углах эпюры), при этом знак фактора (плюс или минус) не указываются.
На положительной области (в самой широкой части) ставится знак «+» в кружке, а на отрицательной области – знак «—» в кружке (см. примеры построения эпюр). Иногда знаки «+» и «—» на эпюре указываются сверху и снизу цифры « 0 » (справа нулевой линии), тогда на площади графика эпюры эти знаки (в кружках) не ставятся.

По окончании построения эпюры по ее площади проводят тонкие вертикальные линии через равные промежутки. Эти линии символизируют сечения бруса. Иногда, в случае построения сложной пространственной эпюры, линии выполняют не вертикально, а в соответствии с проекционным направлением участка на графике эпюры.

Определение знака фактора на эпюре

При построении эпюр внутренних силовых факторов или деформаций необходимо правильно определять знак фактора на данном силовом участке бруса. Для этого следует пользоваться следующими общепринятыми правилами:

Особенности построения эпюр поперечных сил и изгибающих моментов

Для облегчения построения эпюр и контроля правильности графика следует запомнить ряд правил, вытекающих из теоремы Журавского:

На участке, где равномерно распределенная нагрузка q отсутствует, эпюра поперечных сил Q представляет собой прямую линию, параллельную нулевой линии (оси бруса), а эпюра изгибающих моментов M_из – наклонную прямую.

В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть ступенчатый скачок на величину этой силы, а на эпюре M_из – излом (изменение направления графика).

На участке действия равномерно распределенной нагрузки q эпюра Q представляет собой наклонную прямую, а эпюра M_из – параболу, обращенную выпуклостью навстречу стрелкам, изображающим направление распределенной нагрузки.

Если эпюра Q на наклонном участке в каком-либо сечении пересекает нулевую линию эпюры, то в этом сечении на эпюре изгибающих моментов M_из будет иметь экстремальное значение (минимальное или максимальное).

Если на границе действия распределенной нагрузки нет сосредоточенных сил, то наклонный участок эпюры Q соединяется с горизонтальным без «ступеньки», а параболический участок эпюры M_из соединяется с наклонным участком плавно, без излома.

В сечениях, где к брусу приложены сосредоченные пары сил, на эпюре M_из будут иметь место ступенчатые скачки на величину действующих внешних моментов, а эпюра Q изменения не претерпевает (приложенные к брусу изгибающие моменты не влияют на эпюру поперечных сил).

Примеры построения эпюр

Материалы раздела «Сопротивление материалов»:

Источник