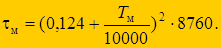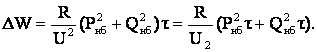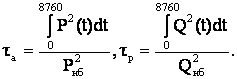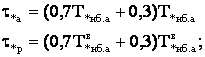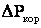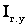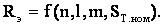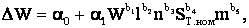Что такое время максимальных потерь
Определение времени максимальной нагрузки; времени максимальных потерь; формулы для их расчета.
Для характеристики графика пользуются временем использования максимальной нагрузки Tmax. Это время, в течение которого при работе установки с максимальной нагрузкой из сети потребляется такое же количество электроэнергии, что и по реальному графику нагрузки. Значение Tmax можно рассчитать следующим образом:
Для типовых графиков нагрузки величина τм определяется по известной величине Tм:
Величина τмв рассчитывается по формуле (7.3) по величине Tмв, значение которой определяется как средневзвешенное:
Данная зависимость не учитывает изменение коэффициента мощности нагрузки, что было уточнено А.А.Глазуновым при построении кривых, представленных на рис.5.6. При этом предполагается, что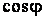 
нагрузки остается неизменным в течение года.
Зависимость времени максимальных потерь от параметров, характеризующих конфигурацию годового графика передаваемой активной мощности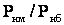 
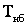
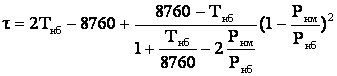
и 
, устанавливает следующая формула
. (5.38)
Фактически по методу времени максимальных потерь можно рассчитать потери электроэнергии только за годовой период времени. Он используется при проектировании электрических сетей, а также в процессе эксплуатации при отсутствии точных графиков нагрузки и более предпочтителен в радиальных сетях.
Метод раздельного времени максимальных потерь. Для его обоснования перепишем формулу (5.35) в виде:
При различных по форме графиках активной и реактивной нагрузки (изменении 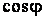во времени) вводится раздельное время максимальных потерь по активной и реактивной мощности:
Недостатком этого подхода является необходимость знания графиков реактивной нагрузки. Анализ большого числа таких графиков позволил получить эмпирические зависимости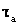 
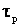
и 
от времени использования наибольшей активной мощности [45]:
где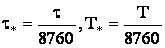 
.
Для коммунально-бытовой и сельскохозяйственной нагрузки коэффициент в=0,75.
Рассмотрим применение описанных методов для расчета потерь электроэнергии в различных элементах сети – линии электропередачи, трансформаторах, компенсирующих устройствах.
Потери электроэнергии в активном сопротивлении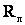 
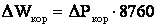
воздушной или кабельной линии можно рассчитать любым методом, рассмотренным в данном параграфе, в зависимости от имеющейся исходной информации. Годовые потери электроэнергии на корону в воздушных линиях обычно оценивают по среднегодовым потерям мощности 
. (5.39)
Общие годовые потери электроэнергии, например, с использованием метода времени максимальных потерь составят
. (5.40)
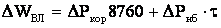
Как отмечалось, в кабельных линиях высокого напряжения следует учитывать потери активной мощности в изоляции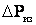 
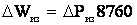
. Вызванные ими годовые потери электроэнергии равны
. (5.41)
В трансформаторах потери электроэнергии состоят из потерь в обмотках и стали магнитопровода (потери холостого хода).
Потери в обмотках можно найти одним из методов, приведенном в данном параграфе.
Потери активной мощности холостого хода, которые для конкретного трансформатора зависят только от уровня напряжения, можно считать постоянными и обусловленные ими годовые потери электроэнергии определяют по формуле
(5.42)
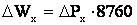
Общие годовые потери электроэнергии в двухобмоточном трансформаторе на основании метода времени максимальных потерь можно записать
. (5.43)
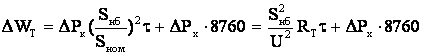
Для трансформатора с расщепленной обмоткой при раздельной работе обмоток низшего напряжения (см. рис.5.2) общие годовые потери электроэнергии составят
, (5.44)
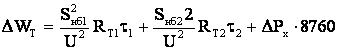
где индексами 1 и 2 обозначены величины, относящиеся соответственно к ветвям схемы замещения с сопротивлениями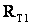 
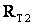
и 
.
В трехобмоточных трансформаторах и автотрансформаторах в общем случае по каждой обмотке передается разная мощность. При этом в понижающем режиме, когда мощность от обмотки высшего напряжения передается в обмотки среднего и низшего напряжений (см. рис.5.3), время максимальных потерь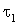 
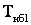
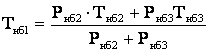
обмотки высшего напряжения можно найти на основании формулы (5.37) по времени использования наибольшей нагрузки этой обмотки 
, которое рассчитывается по выражению
, (5.45)
где индексами 2 и 3 обозначены величины, относящиеся соответственно к обмоткам среднего и низшего напряжения.
С учетом изложенного общие годовые потери электроэнергии в трехобмоточном трансформаторе или автотрансформаторе равны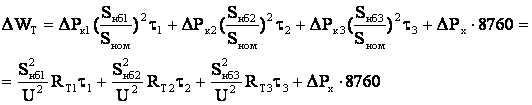 
. (5.46)
Потери активной мощности в батареях конденсаторов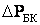 
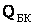
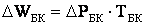
зависят от их включенной мощности 
и определяются формулой (5.22). В общем случае потери электроэнергии в них можно оценить по выражению
, (5.47)
где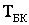 
— время работы батареи конденсаторов за расчетный период (год).
Аналогично находят потери электроэнергии в шунтирующих реакторах
, (5.48)
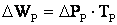
где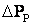 
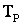
— потери активной мощности в реакторе; 
— время работы реактора в течение года.
В синхронных компенсаторах потери активной мощности определяются формулой (5.23), где одна часть потерь не зависит от рабочей мощности компенсатора, а другая часть зависит от нее. В связи с этим потери электроэнергии в них
, (5.49)
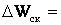
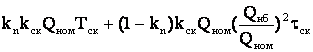
где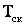 
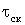
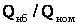
— время работы синхронного компенсатора;
— время максимальных потерь синхронного компенсатора;
— коэффициент загрузки синхронного компенсатора в максимальном режиме.
Метод эквивалентного сопротивления. Рассмотренные ранее методы определения потерь электроэнергии мало пригодны для разветвленных распределительных сетей 6-20 кВ (рис.5.7, а). Это объясняется тем, что при поэлементном расчете потерь для каждого участка сети необходимо иметь режимную информацию, которую в реальных условиях проектирования и эксплуатации сети получить невозможно. Она обычно известна лишь на головных участках линий и на трансформаторах, питающих сеть.
В соответствии с методом эквивалентного сопротивления [44] реальная сеть заменяется некоторой эквивалентной сетью (рис.5.7, б) с таким сопротивлением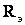 
, в котором выделяются те же потери мощности и энергии, что и в реальной сети.
Для такой сети потери мощности находятся по току головного участка 
,
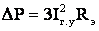
а потери энергии – по методу времени максимальных потерь
.
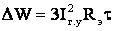
В общем случае эквивалентное сопротивление зависит от количества n и длин l участков линий, количества m и мощности распределительных трансформаторов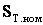 
:
Вероятностно-статистический метод. Он также используется для расчета потерь электроэнергии в разветвленных распределительных сетях 6-20 кВ. Согласно этому методу предварительно на основании вычислительных экспериментов для большого количества различных сетей устанавливается связь между потерями электроэнергии с одной стороны и параметрами сети с другой стороны:
где W – отпуск электроэнергии в сеть;
n – количество участков линий;
— суммарная мощность распределительных трансформаторов;
— коэффициенты.
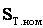
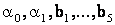
Зная приведенные коэффициенты для любой сети с соответствующими параметрами, нетрудно найти годовые потери электроэнергии.
Чтобы распечатать файл, скачайте его (в формате Word).
Годовые графики по продолжительности. Годовое число часов использования максимума нагрузок, время максимальных потерь
Имея суточные графики для зимы и лета, можно построить годовой график нагрузки станции (п/с). Такой график называется графиком по продолжительности. Для этого условно принимают продолжительность зимнего периода 200 дней, а летнего 165. По оси ординат годового графика по продолжительности в соответствующем масштабе откладывают нагрузки от РМАКС до РМИН, а по оси абсцисс – часы года от 0 до 8760 (24*365=8760). Площадь годового графика выражает количество потребленной электроэнергии за год.
На основании годового графиков нагрузок могут быть определены некоторые коэффициенты, которыми пользуются при проектировании и эксплуатации электрических установок:
Графики электрических нагрузок предприятий различных отраслей промышленности, городов, рабочих поселков позволяют прогнозировать ожидаемые максимальные нагрузки, режим и размеры потребления ЭЭ, обоснованно проектировать развитие системы. Чем равномернее графики нагрузки потребителей, тем равномернее и график нагрузки электрической системы в целом, тем легче обеспечить экономичную работу электростанции.
При разработке перспективных годовых графиков различают статические графики, отображающие изменение нагрузки в течение года при заданном постоянном составе потребителей, и динамические графики, учитывающие рост нагрузки, обусловленный вводом в эксплуатацию новых потребителей.
Метод времени максимальных потерь
Изменения нагрузок во времени в течение года обычно представляют в виде упорядоченной диаграммы по снижению максимумов (рис. 6.1). Выражение для нагрузочных потерь энергии с использованием этой диаграммы можно записать в виде
, (6.7)
где DPmax – потери мощности в режиме максимальных нагрузок (на первой ступени диаграммы),
, (6.8)
где Smaxи Imax – соответственно мощность и ток в элементе сети в режиме максимальных нагрузок.
. (6.9)
. (6.10)
Величина t называется временем максимальных потерь.Исходя из формулы (6.10) можно дать следующее определение: время максимальных потерь–это время, за которое в элементе сети, работающем с максимальной нагрузкой, выделятся те же нагрузочные потери энергии, что и при работе по реальному графику нагрузки за год.
,
то при U = const и cosj = const потери мощности в формуле (6.9) можно заменить квадратами активных мощностей:
. (6.11)
Одной из характеристик годового графика (упорядоченной диаграммы по снижению максимумов) активной мощности является время использования максимума нагрузки Тmax– это время, в течение которого потребитель или элемент сети, работающий с максимальной нагрузкой, израсходует или передаст столько же энергии, сколько он расходует или передает при реальной работе за год.
В соответствии с этим определением, величину Тmaxможно вычислить следующим образом:
, (6.12)
где W –энергия, передаваемая за год через данный элемент сети и равная площади под годовым графиком активной мощности. Из данной формулы следует, что эта площадь должна быть равна площади прямоугольника, ограниченного прямыми Р = Рmaxи t = Тmax,а также осями координат (рис. 6.1).
Величины Тmax и t определяются по похожим выражениям, однако время максимальных потерь рассчитывается через квадраты, а время использования максимума нагрузки – через первые степени мощностей. Так как 
,то t £ Tmax(равенство имеет место при одноступенчатом годовом графике).
Таким образом, между временем максимальных потерь и временем использования максимума нагрузки не существует однозначной зависимости (одному и тому значению Тmaxмогут соответствовать разные значения t). Вместе с тем между этими величинами существует корреляционная связь, которая выражается приближенной формулой
. (6.13)
Это выражение положено в основу метода времени максимальных потерь.
|
|
|
|
|
|
|
Рис. 7.3. Годовая упорядоченная диаграмма активной мощности по снижению максимумов
1. Рассчитываются величины t и ΔРmaxпо формулам (6.13) и (6.8) для каждого элемента сети. Время использования максимума нагрузки определяется по справочным данным либо по годовому графику активной мощности; максимальная передаваемая мощность определяется расчетным путем или на основе измерений;
2. Вычисляются нагрузочные потери энергии в каждом элементе сети по выражению (6.10);
3. Определяются условно-постоянные потери энергии в каждом элементе сети по формуле (6.2);
4. Вычисляются суммарные потери энергии.
Основное достоинство метода времени максимальных потерь перед методом средних нагрузок состоит в том, что для расчета потерь не требуется проводить измерения. Поэтому данный метод можно использовать не только при эксплуатации, но и при проектировании электрических сетей. Недостаток – пониженная точность расчета.
Погрешности метода времени максимальных потерь обусловлены
2. Использованием приближенной формулы (6.13).
Основная область применения данного метода – питающие электрические сети.
Время использования максимальных нагрузок
Время использования максимальных нагрузок определяется по годовому графику по продолжительности за рассматриваемый промежуток времени.
Годовое число часов использования максимума активной нагрузки – это отношение годового расхода активной электроэнергии к получасовой максимальной мощности:
, (3.12)
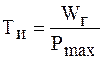
где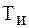 
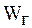
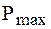
– годовое число часов использования максимальной активной нагрузки, ч; 
– годовой расход активной электроэнергии, кВт·ч; 
– получасовая максимальная мощность, кВт.
По времени использования максимальных нагрузок определяется согласно [1] экономическая плотность тока при выборе проводников.
Для удобства инженерных расчётов электрических нагрузок коэффициенты, характеризующие графики нагрузок индивидуальных ЭП, аналитические выражения для их определения и соотношения между этими коэффициентами приведены в табл. 3.1, а коэффициенты, характеризующие графики нагрузок группы ЭП, – в табл. 3.2. В этих таблицах все коэффициенты записаны применительно к активной мощности. Определение коэффициентов по реактивной мощности и току производится аналогично приведённым формулам.
Коэффициенты, используемые при расчёте нагрузок
| Коэффициент | Обозначение | Для одиночного ЭП |
| Включения |  |  |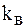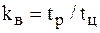
| Использования |  |  |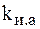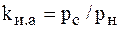
| Загрузки |  |  |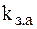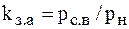
| Формы графика |  |  |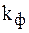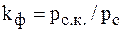
Коэффициенты, используемые при расчёте электрических нагрузок