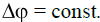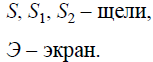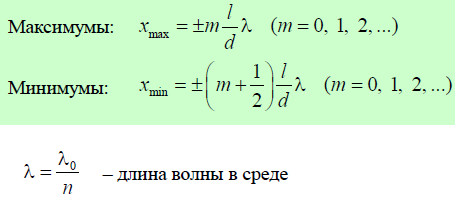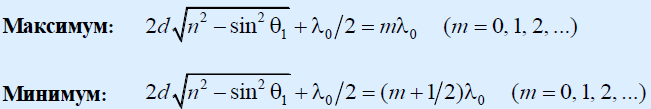Что такое время когерентности длина когерентности

Световых волн. Временная когерентность. Время и длина когерентности.

Интерференция света – пространственное перераспределение энергии светового излучения при наложении когерентных световых волн.

Когерентностью называется согласованное протекание двух или нескольких колебательных или волновых процессов (см. лекцию № 28, п.3).

Монохроматическое излучение (от греч. monos – один, единый и chroma – цвет) – электромагнитное излучение одной определенной и строго постоянной частоты. Происхождение термина связано с тем, что различие в частоте световых волн воспринимается человеком как различие в цвете. Отметим, что излучаемый реальным источником свет не может быть строго монохроматичным.

Различают временную и пространственную когерентность.

Временная когерентностьхарактеризует сохранение взаимной когерентности при временном отставании одного из лучей по отношению к другому.Мерой когерентностислужит время когерентности — максимально возможное время отставания одного луча по отношению к другому, при котором их взаимная когерентность еще сохраняется.

В идеализированном случае рассматривают интерференцию строго монохроматических волн с постоянной разностью фаз. Однако, такие волны бесконечны в пространстве, времени и, не существуют в природе. Поэтому интерференция монохроматических волн является лишь первым приближением в изучении интерференции волн от реальных источников.

Выясним роль немонохроматичности волн во временной когерентности.

При рассмотрении интерференции близкий к монохроматическому реальный свет можно представить как набор монохроматических составляющих – волн в интервале частот от ω до ω + Δω. где Δω – достаточно малая величина. Пусть волны, соответствующие крайним значениям спектрального интервала (ω; ω + Δω) вызывают в данной точке пространства (например, на экране) колебания ωt и (ω + Δω)t (начальные фазы для простоты полагаем равными нулю). Если разность фаз составляющих (компонент) кратных частот в этой точке равна π, то это означает, что на «горб» от одной составляющей наложится «впадина» от другой крайней компоненты (ω + Δω) Интерференционная картина «смажется». Наглядно представить ситуацию можно следующим образом. Наложите ладонь одной руки на ладонь другой, палец на палец, а теперь сместите одну из ладоней на ширину одного пальца, картина интенсивности сладится.

(Замечание. Рассмотрение промежуточных по частоте компонент между ω и ω + Δω не изменит качественной картины.)

Итак, время, за которое разность фаз компонент световой волны с верхней и нижней частотой составит порядка π и будет временем когерентности. Разность фаз этих колебаний Δφ = Δωt. Время когерентности определится из соотношения Δω ≈π. Так как Δω = 2πΔν , то 2πΔν ≈π. Отсюда ≈1/2Δν, пренебрегая в наших оценках «двойкой», получим

≈

От частоты перейдем к длине волны ν = с / λ. Продифференцируем последнее выражение: dν = – и заменим знак дифференциала d на Δ, полагая изменение λ конечным, но достаточно малым.

≈

Модуль = .

Соответственно время когерентности

где Δλ – ширина интервала длин интерферирующих волн; чем меньше интервал Δλ, тем больше время когерентности.

Можно сказать, что в тех случаях, когда время фиксирования интерференционной картины много больше времени когерентности накладываемых волн ( >> ), прибор не зафиксирует интерференции. Если же

Мерой пространственной когерентности служит радиус когерентности – наибольший радиус круга, мысленно вырезаемый в поперечном сечении волны, при котором любые два луча, исходящие из различных точек внутри этого круга, еще остаются взаимокогерентными.

Если размеры источника значительно меньше длины световой волны, то всегда получается резкая интерференционная картина (лучи идут, по существу, из одной точки).

В случае источника конечных размеров получаем, по существу, наложение многих интерференционных картин, создаваемых многими парами когерентных источников.

стности полос до их практически полного размытия. Пусть расстояние между отверстиями ρ. Рассмотрим излучение в направлении угла φ (волновые вектора и ). Разность хода волн Δ = ρsinφ. В случае малого угла φ можно заменить sinφ на φ, тогда Δ = ρφ. Соответствующая этой разности хода разность фаз лучей и

δ = kΔ = ρφ.

Исходя из выше сказанного, приравняем ρφ≈π. Максимальный угол φ в одну сторону φ = . Учитывая излучение от одной щели по обе стороны от нормали к щели ( и ), получим Δφ = 2φ = 2λ /2ρ = λ / ρ. Согласно данному в начале пункта определения радиуса когерентности, из последнего соотношения получаем радиус когерентности

Соотношение (32-3) является ограничением размеров источника.

Пример. Имеется некоторый светящийся предмет размером d (рис. 32.2),

можно оценить как d≈ Δφ. Из соотношения (32-3) Δφ ≈λ / ρ, тогда d ≈ То есть, размеры предметы должны быть

Источник

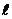
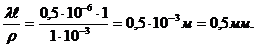
Когерентность волн

В этой статье мы расскажем, что означает понятие когерентности, определим ее основные виды (временная и пространственная), а также решим несколько задач, связанных с оценкой когерентности. Начнем с базового определения.

При наблюдении интерференции волн одним из важнейших условий является их когерентность. О наличии когерентности говорят тогда, когда имеет место согласованность протекания волновых или колебательных процессов во времени и пространстве.

Когерентность характеризуется такой чертой, как степень (иначе ее можно назвать степенью согласованности вышеуказанных процессов). Различают два основных типа данного явления – временную и пространственную когерентность.

Что такое временная когерентность

Данный тип когерентности характеризуется длиной и продолжительностью. Она возникает тогда, когда мы имеем дело с немонохромным точечным источником света. Примером могут быть полосы, наблюдаемые при интерференции в специальном приборе – интерферометре Майкельсона: чем выше оптическая разность, тем менее четкими становятся полосы (вплоть до полного исчезновения). Основная причина временной когерентности света лежит в длине источника и конечном времени свечения.

В таком случае исследуемые волны когерентными не являются. Если же за указанное время величина cos δ ( t ) сохраняется практически неизменной, то интерференция становится очевидной, и у нас получаются когерентные волны.

Из всего этого можно сделать вывод об относительности понятия когерентности. При малой инерционности прибора интерференция, как правило, обнаруживается, а если прибор обладает большим временем инерции, то нужную картину мы можем просто не увидеть.

Время когерентности имеет зависимость от интервала частот, а также от длины волн, представленных в общей световой волне.

Что такое пространственная когерентность

Если мы имеем дело с монохроматическим протяженным, а не точечным источником света, то здесь вводится понятие пространственной когерентности. Она имеет такие характеристики, как ширина, радиус и угол.

Буквой φ обозначен угловой размер источника световой волны.

Если волна света располагается вблизи нагретого тела, то ее пространственная когерентность составляет всего несколько длин волн. Чем больше расстояние от источника света, тем выше степень пространственной когерентности.

Чтобы оценить радиус когерентности, воспользуемся формулой ρ k o g

Интерференция солнечных лучей не может быть видна невооруженным взглядом, поскольку радиус ее когерентности очень мал и находится вне разрешающей способности человеческого глаза.

Условие: если два не связанных между собой источника света испускают волны, почему данные волны не будут когерентными?

Источник

Когерентность. Временной и спектральный подход к анализу интерференции. Время когерентности, длина когерентности.

Когерентность:Волны называют когерентными, если не изменяется с течением времени разность фаз складываемых волн, т.е.

Способы получения интерференции света: метод Юнга, зеркала Френеля, бипризма Френеля. Интерференция света в опыте Юнга: положение максимумов и минимумов освещенности. Пространственная когерентность, радиус когерентности.

Интерференция света в опыте Юнга: положение максимумов и минимумов освещенности. Пространственная когерентность, радиус когерентности:

Условия от двух источников:

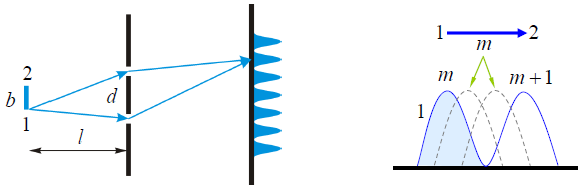
Интерференция не наблюдается (картина смазанная), если максимум (m+1)–го порядка от точки 1 совпадает с максимумом m–го порядка от точки 2.

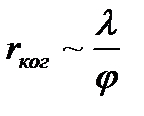
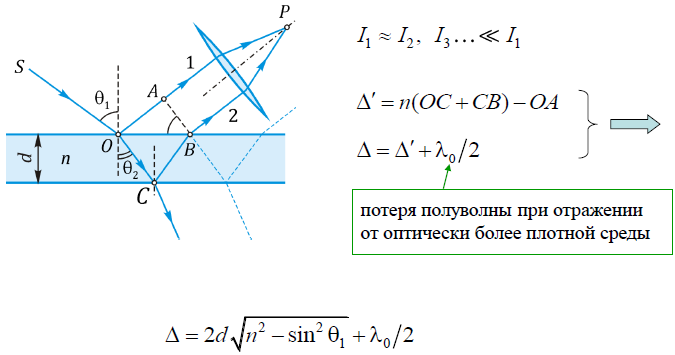
Радиусом когерентности: (или длиной пространственной когерентности) называется максимальное, поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. где λ – длина волны света, φ – угловой размер источника.

Интерференция света в тонких пленках. Условия максимумов и минимумов интерференции. Полосы равной толщины и равного наклона, кольца Ньютона.

Интерференция света в тонких пленках:

Условия максимумов и минимумов интерференции:

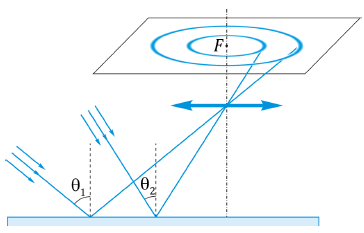
Полосы равной толщины и равного наклона:

Тонкая пластинка освещается рассеянным монохроматическим светом.

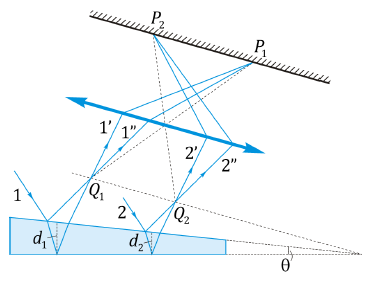
Тонкая пластинка в виде клина освещается

плоской световой волной.

полос равной толщины.

Кольца Ньютона:

Источник

4.3. Когерентность

Известно, что строго монохроматический свет – это идеализация. Реальный свет, как бы мы не старались его монохроматизировать, остаётся в той или иной степени немонохроматическим, представляющим собой набор монохроматических компонент в некотором конечном интервале длин волн (l, l + Dl). Примем, что эти монохроматические компоненты равномерно заполняют указанный интервал.

Как показывает формула (), ширина полос DX

l. Изобразим положения максимумов для волн, соответствующих крайним значениям спектрального интервала (l, l + Dl) сплошными отрезками — для l, пунктирными – для l + Dl (рис. ). Максимумы же от промежуточных длин волн заполняют интервал между крайними максимумами каждого порядка интерференции.

В результате промежуточные максимумы, как видно из рис. 1 будут постоянно заполнять интервал между максимумами соседних порядков для l и l + Dl. А это значит, что результирующие максимумы (нижняя часть рисунка) будут постоянно размываться, и качество интерференционной картины станет хуже. Отчётливость интерференционной картины количественно характеризуется её видимостью:

(1)

Максимальная видимость (V = 1) достигается при Jmin = 0, а минимальная (V = 0) – при Jmax = Jmin, т. е. когда интерференционная картина отсутствует.

С помощью рис. можно заключить, что полосы исчезнут там, где M(l + Dl) » (M + 1)l, здесь M – предельный порядок интерференции, начиная с которого полосы исчезают. Отсюда:

(2)

Величина l/Dl характеризует Степень монохроматичности Света: чем она больше, тем больше и степень монохроматичности.

Таким образом, мы нашли то значение M, при котором картина интерференции исчезает, т. е. складываемые колебания становятся уже некогерентными. Найденное значение M () определяет так называемую Длину когерентности:

. Отсюда следует, что

(3)

Видно, что длина когерентности световой волны непосредственно связана со степенью монохроматичности (l/Dl): чем больше последняя, тем больше и длина когерентности. Для солнечного света Lcog » 5l, для лучших (не лазерных) источников света удалось получить Lcog порядка нескольких десятков сантиметров. Лазеры позволили получить излучение с Lcog порядка сотен метров (и даже нескольких километров).

Итак, можно утверждать, что для получения интерференционной картины необходимо, чтобы оптическая разность хода складываемых колебаний была меньше длины когерентности:

Это требование касается Всех Установок, с помощью которых мы хотим наблюдать картину интерференции.

В заключение заметим, что длина когерентности связана с так называемым Временем когерентности TCog – промежуток времени, в течение которого случайные изменения фазы световой волны в данной точке достигают значения порядка p. За это время волна распространяется на расстояние порядка Lcog = CTCog.

До сих пор размер источников предполагался малым (часто говорят точечный источник). Увеличение размеров источника, как и уменьшение степени монохроматичности света приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению.

1. Рассмотрим первую экспериментальную установку для демонстрации интерференции, предложенную Юнгом (опыт Юнга). В ней яркий пучок света освещал узкую щель S (рис. ). Прошедший через щель свет вследствие дифракции образует расходящуюся волну, которая падает на две узкие щели S1 и S2. Эти щели действуют как вторичные когерентные источники и, исходящие из них дифрагированные волны, перекрываясь, дают на экране Э систему интерференционных полос.

Для получения устойчивой во времени интерференционной картины необходимо, чтобы геометрия установки удовлетворяла определённым условиям, связанным со свойствами используемого излучения. Эти свойства, во-первых, задавались Длиной когерентности, что связано с монохроматичностью источника. Во-вторых – Шириной когерентности.

Что представляет собой ширина когерентности рассмотрим на примере опыта Юнга, предположив, что излучение источника S монохроматично, но щель имеет конечную ширину. Расширение щели, как и уменьшение степени монохроматичности света приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению.

При увеличении ширины щели S расстояния между максимумами от её крайних элементов будут увеличиваться, т. е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели. Если положить для простоты расстояния A = B, тогда при ширине щели S, равной ширине интерференционной полосы DX, интервал между соседними максимумами от края 1 будет целиком заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.

Но это явление можно объяснить и иначе, а именно, интерференционная картина исчезает вследствие того, что вторичные источники – щели S1 и S2 – становятся некогерентными. Это позволяет говорить о Ширине когерентности (Hcog) падающей на щели S1 и S2 световой волны от S, где отдельные участки волны в достаточной степени когерентны между собой.

Найдём формулу для вычисления Hcog. В рассматриваемой схеме запишем условие, при котором щели S1 и S2 становятся некогерентными источниками:

, (4)

Где D – расстояние между щелями. Кроме того, выяснили, что картина исчезнет, когда ширина щели S » DX. Ширина же полосы, согласно (6), равна:

; (5)

Из этих трёх равенств получим:

, (6)

Где j — угловая ширина щели S относительно диафрагмы с двумя щелями (в опыте Юнга).

Если в качестве источника использовать Непосредственно Солнце (его угловой размер j » 0,01 рад и l » 0,5 мкм), то ширина когерентности, согласно (6), Hcog » 0,05 мм. Поэтому для получения интерференционной картины от двух щелей с помощью такого излучателя расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.

Итак, для получения устойчивой интерференционной картины с использованием обычных (не лазерных) источников света необходимо исходную световую волну расщепить подходящим способом на две части, которые затем в области перекрытия и образуют систему полос, но лишь в том случае, если у исходной световой волны:

1) длина когерентности LCog превышает оптическую разность хода складываемых колебаний;

2) ширина когерентности Hcog превышает расстояние D между щелями.

Насколько большими должны быть эти величины, общепринятого соглашения нет. Это зависит от желаемого значения параметра видности.

Заметим также, что в разных интерференционных схемах под D надо понимать расстояния между некоторыми характерными лучами в месте расщепления исходной световой волны.

Источник