Что такое время интегрирования
Методика настройки цифрового ПИД-регулятора
Методика настройки цифрового ПИД-регулятора
Обычно, при использовании пропорционально-интегрально-дифференциального или ПИД- (PID- Proportional-Integral-Derivative) регулятора и грамотной его настройке, достигается лучшая точность управления по сравнению с двухпозиционным (релейным) регулятором. Но для оптимальной настройки регулятора и, как следствие, получение желаемого качества управления, необходимо понимание механизмов и принципов работы ПИД-регулятора.
При ПИД-регулировании сигнал управления зависит не только от разницы между текущим и заданным значением (величины ошибки или рассогласования), а также от накопленной ошибки (интеграла) и от скорости изменения ошибки во времени (дифференциала). В результате ПИД-регулятор обеспечивает такое значение сигнала управления, при котором ошибка в установившемся режиме стремится к нулю. Качество управления определяется многими факторами, ключевыми являются недетерминированность объекта управления, точность ввода-вывода регулятора и интенсивность внешних воздействий.
Настройка пропорциональной компоненты (Xp)
Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются, постоянная интегрирования устанавливается максимально возможной (Ти = макс), а постоянная дифференцирования минимально возможной (Тд = 0). Устанавливается безопасная величина уставки, равная (0,7…0,9)×SP, где SP – это реальная уставка настраиваемой системы. Зона пропорциональности устанавливается минимально возможной (Xp = 0).
В этом случае регулятор выполняет функции двухпозиционного релейного регулятора с гистерезисом равным нулю. Регистрируется переходная характеристика.
Настройка дифференциальной компоненты (Tд)
Этот этап присутствует только в том случае, если применяется полнофункциональный ПИД-регулятор. Если дифференциальная компонента применяться не будет (используется пропорционально-интегральный (ПИ) регулятор), то следует пропустить этот этап.
На предыдущем этапе была задана зона пропорциональности, соответствующая переходной характеристике типа 2, в которой присутствуют затухающие колебания (см. рис. 3, кривая 2, рис. 4, кривая 1.).
| Рис. 4 |
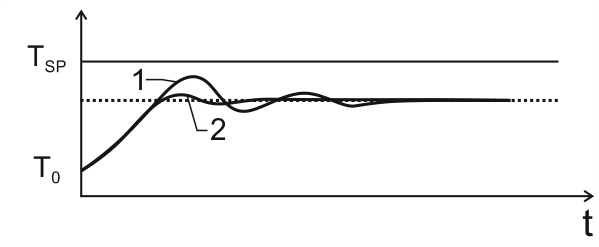 |
Следует установить постоянную времени дифференцирования Тд так, чтобы переходная характеристика имела вид кривой 2 на рис. 4. В качестве первого приближения постоянная времени дифференцирования делается равной Тд = 0,2×∆t.
Примечательно то, что дифференциальная компонента устраняет затухающие колебания и делает переходную характеристику, похожей на тип 3 (см. рис. 3). При этом зона пропорциональности меньше, чем для типа 3. Это значит, что динамическая и статическая точность регулирования при наличии дифференциальной компоненты (ПД-регулятор) может быть выше, чем для П-регулятора.
Настройка интегральной компоненты (Ти )
После настройки пропорциональной компоненты (а при необходимости и дифференциальной компоненты) получается переходная характеристика, показанная на следующем рисунке, кривая 1.
ПИД-регулятор своими руками
I. Постановка задачи
II. Теоретическая вводная
Как получается ПИД-регулятор? Берём разницу между текущей температурой и нужной, умножаем на настраиваемый коэффициент, получаем мощность, которую надо выдать в данный момент. Это пропорциональная составляющая, она работает в момент появления рассогласования — то есть моментально откликается как на изменение уставки, так и на поведение объекта. Начал подогреваться? Мощность начинает спадать. Перегрелся? Выключилось, или даже дали сигнал охлаждения. Всё хорошо, вот только в реальной жизни эффект от воздействия проявляется с запаздыванием, а на объект воздействуем не только мы, но еще и окружающая среда: разогретый реактор не только внутри горячий, но еще и остывает, отдавая тепло комнате, а потому как только выключаем мощность, он сразу начинает остывать. Поэтому чистый пропорциональный регулятор колеблется вокруг точки поддержания, и тем сильнее колеблется, чем выше воздействие окружающей среды / содержимого реактора.
Чтобы компенсировать «внешние» воздействия на реактор, в цепь добавляют интегральную составляющую. Всё рассогласование, которое было в системе, идёт на интегратор (соответственно, как только мы перегрели — сумма уменьшается, пока недогрето — сумма увеличивается). И накопленный интеграл, со своим коэффициентом, даёт свою прибавку-убавку к мощности. В результате такого подхода, при стационарном процессе, через некоторое время интеграл подбирает такой вклад в сумму с мощностью, который компенсирует потери окружающей среды, и колебания исчезают — интеграл становится стабильным, поэтому величина выдаваемой мощности становится постоянной. Причем так как при этом держится нужная температура, рассогласование отсутствует, пропорциональная составляющая не работает вообще.
Для компенсации влияния задержек между воздействием и реакцией системы, в систему добавляют дифференциальную составляющую. Просто пропорциональный регулятор даёт мощность всё время, пока температура не достигнет нужной точки, пропорционально-дифференциальный начинает снижать подаваемую мощность раньше, чем догрелся до нужной точки — так как рассогласование уменьшается, имеется наличие отрицательной производной, уменьшающей воздействие. Это позволяет минимизировать перегрев при больших переходах.
Итак, с физическим смыслом разобрались, перейдём к основым вопросам реализации.
III. Кому пользоваться регулятором?
Что из этого следует? Из этого следует, что техники понимают физическую составляющую, и имеют опыт настройки аппаратных пид регуляторов. А значит, программная реализация должна исходить из удобства настройки техниками — повторяя физическую модель. И это крайне важно! Очень часто в угоду упрощения кода коэффициенты меняют, например, на обратные — чтобы избавиться от деления. В результате, настройка превращается в ад и кошмар, и требуется опыт настройки данного конкретного регулятора, вместо понимания процесса. Отсюда получаем, что наши коэффициенты — постоянная интегрирования и постоянная дифференцирования — должны иметь размерность времени, то есть задаваться в секундах, а никак не в «1/с», как это любят делать.
IV. Область функционирования.
1200°C, управляется только подача мощности.
Точность управления определяется во-1х точностью измерения: градуировочные таблицы даны через 0.1 градуса; линейность внутри таблиц в принципе достойная, поэтому точность ограничена в первую очередь усилителем и измерителем тока. В моём случае, хотелось добиться точности поддержания 0.1 градуса, поэтому измеритель настроен на 1/32 градуса: это даёт
V. Диапазон настраиваемости.
Для управления микрореактором с мощной силовой установкой может оказаться что для нагрева на 10 градусов достаточно 1% мощности, в то время как для большой инертной печи для того чтобы подогреть на градус едва-едва хватает 100% мощности подогрева. (В реальной жизни, это выглядит так — есть несколько подогревателей с ручным управлением — они включаются отдельным рубильником и производят начальный нагрев, в дальнейшем поддержание рабочей точки обеспечивает терморегулятор, управляя еще одним подогревателем, который на полной мощности выдаёт максимум +10°C к тому, что нагрели постоянно включенные). Исходя из этого, предельным коэффициентом пропорциональности логично предположить 100% мощности на 1 градус. Больше не имеет смысла, так как мы хотим получить управляемость в 0.1 градуса. Минимальный, для простоты, я взял инверсным — 1% мощности на 100 градусов.
Диапазоны временных коэффициентов вычисляются просто исходя из наших условий работы регулятора. Так как мы управляем через мощностью симистор путём вычисления задержки момента включения после прохождения через 0, предельная частота работы регулятора — 50Гц. Если мы уверены, что управляем мощностью которой пофиг плюс или минус, мы можем работать на 100Гц, но это не всегда так, и потому лучше каждый раз дозировать равное количество как положительной так и отрицательной полуволны. Для упрощения жизни, я снизил время работы до 25Гц, тем самым любое вычисленное воздействие будет действовать в течение 4 полуволн, и за это время у меня будет возможность рассчитать новое воздействие.
Таким образом, постоянные времени задаются через 1/25 сек, от 0 до
2000 сек (2000*25 = 50000, как раз в 16бит влазит).
Ну и еще у нас есть ограничение мощности минимальное и максимальное, от 0 до 100%.
VI. Управление мощностью.
Начиная с этого момента все теоретические выкладки заканчиваются, начинается горькая практика, привязанная к конкретной реализации.
Итак, мы уже решили что управляем задержкой открывания симистора после прохождения через 0. Таким образом, задержка в 0 означает 100% мощность, бесконечная задержка = 0% мощности.
Вопрос: с какой точностью мы можем управлять мощностью? Вообще, с точностью отсчета времени нашего таймера. С другой стороны, какая нужна мощность? Мы вычисляем какой % мощности нужно подать на 0.04сек. В принципе, по опыту, управления мощностью даже с точностью в 1% на частоте в 0.1сек хватает для поддержания температуры в 1 градус. У нас управление 0.04сек (в 2.5раза быстрее). Поэтому было принято решение рассчитать таблицу мощности через 1/250 от максимума (с шагом в 0.4%). Это позволяет таблицу иметь не сильно большую (500 байт), и при этом иметь точность выше 1%. Если ваш случай требует бОльшей точности — пересчитать не так сложно.
Теперь поговорим о расчете этой самой таблицы. Во-1х следует учесть, что есть момент срабатывания сигнала прохождения через ноль. В моем случае — 12В. То есть когда входное напряжение упадёт ниже 12В, я получу сигнал прохождения через 0.
Это означает, что для 100% мощности время запуска = времени прохождения 12В.
Процессор у меня работает на частоте 32786, PLL настроен на 384/2, полуволна имеет 100Гц, откуда получаем, что код для загрузки константы в таймер для времени T имеет вид:
Нам нужно рассчитать время задержки, дающее равномерное увеличение площади включенной части синусоиды. То есть нам нужно иметь отсчеты времени, дающие равномерное увеличение мощности. Полная мощность, которую мы выдаём — это интеграл по всей синусоиде. [кто знает, как на хабре формулы вставлять? никак? пишу в maple-нотации тогда].
Таким образом, нам нужно пройтись по всем Q с заданной точностью, и для каждой из них найти T.
Я для себя это решил вот таким тупым способом:
Всё, на выходе мы получили табличку в 250 значений, соответствующих константам загрузки таймера до момента поджига после получения сигнала о прохождении через 0 (точнее, через 12В, как я говорил выше).
VII. Измерение входных данных
Я пропускаю этот вопрос, потому как он достоен отдельной большой статьи. О том, как я решал вопрос с термосопротивлением, можно найти в архиве почившего в бозе моего блога.
Главное что нам надо знать, это что мы измеряем данные с нужной нам частотой (в данном случае — 25Гц), и нужной точностью (на выходе — число от 0 до 2048 градусов кельвина через 1/32 градуса). Данные предполагаются уже нормализованные для всех дальнейших расчетов.
Если будет кому интересно — пишите в комментах, распишу в следующий раз как это делается для термопар.
VIII. Вычисление воздействия
И вот свершилось: у нас есть все данные для того, чтобы наконец-то произвести то, ради чего мы всё затевали: вычислить какую же мощность следует подать на управляющий элемент.
Вспомним еще раз формулу ПИД регулятора:
U = K * ( Err + (1/Ti)*Int + Td*dErr )
Мы снова пришли к вопросу, который поднимался в разделе III: этим будут пользоваться техники. Поэтомоу крайне важно не допустить классической ошибки всех реализаций — «размерности коэффициентов как получится». Мы делаем прибор для управления физическим процессом, а значит, модель должна соответствовать.
Вот теперь хорошо видно, зачем выносится за скобки пропорциональный коэффициент — это позволяет оставить диф и инт коэффициенты просто постоянными времени, в результате оператор при настройке оперирует простыми и понятными числами — процентом на градус для пропорциональной и секундами для интегральной и дифференциальной коэффициентами.
А благодаря удобному подбору положения точек и размерностей времени, как мы сейчас увидим, все расчеты производятся практически «в лоб».
Кроме одного — у нас есть величина Ti, а для расчета требуется 1/Ti. Операция деления большой разрядности — очень дорогая. Операция умножения в разы дешевле, поэтому воспользуемся отличной статьёй Division by Invariant Integers using Multiplication. У нас ведь K / Ti / Td меняются крайне редко, а потому мы можем себе позволить как угодно извращаться с ними после их изменения, главное чтобы основной цикл расчетов работал быстро.
Таким образом, вместо Ti для расчетов мы раскладываем в набор Ti_m, Ti_sh1, Ti_sh2; и на каждом цикле производим вычисление:
При всех расчетах положение точки вплоть до 7го шага остаётся на 5м справа месте. В последний момент происходит интересный финт ушами. K задаётся через 1/256, соответственно, после умножения точка сдвигается влево до 5+8=13 места, поэтому мы должны у результата отбросить младшие 8 бит. И самый нижний байт результата — нужная нам мощность через 2/5%. Это — еще одна причина, по которой мощность выровнена по шагам в 1/250 — это позволяет результат уложить в один байт и получить легко по таблице нужный результат.
Дальше, помним, что нас интересует мощность только от 0 до 250 — поэтому 7й шаг вычислений идёт очень просто, как только мы получаем отрицательное число — сразу складываем uMin. Как только выяснили что любой старший байт не ноль — сразу складываем uMax. И только если мощность складывается в диапазоне — производим проверку на меньше uMin или больше uMax.
Если вдруг кому интересно:
IX. Применение воздействия.
Итак, у нас есть рассчитанное воздействие, и наша задача — применить его. Для этого работает общий цикл работы с частотой 50Гц. На четном цикле — производится измерение и вычисление, на нечетном — применение воздействия. Таким образом, общая схема получается: выставлена мощность, через одну синусоиду производится измерение и вычисление, еще через одну — применение новой.
X. Подводные камни.
ПИД-регулятор. Методика настройки
2020-07-10 

ПИД-регулятор (пропорционально-интегрально-дифференциальный) — устройство, с обратной связью, применяемое в автоматических системах управления для поддержания заданного значения параметра. Благодаря своей универсальности они широко применяются в различных технологических процессах.
Выходной сигнал регулятора определяется по следующей формуле:
u (t) = P + I + D = Kp e (t) + Ki ∫e (t) dt + Kd de (t)/dt
u (t) – выходной сигнал регулятора;
P – пропорциональная составляющая;
I – интегрирующая составляющая;
D – дифференцирующая составляющая;
Ki — интегральный коэффициент
Kd – дифференциальный коэффициент
e (t) – ошибка рассогласования
Задачи ПИД-регулятора в системах АСУ ТП
Основная задача ПИД регулятора состоит в поддержании определенного значения параметра технологического процесса на заданном уровне. То есть говоря простым языком, задача ПИД-регулятора заключается в том, чтобы учитывая полученные значения с датчиков (обратная связь) воздействовать на объект управления, плавно подводя регулируемое значение к заданным уставкам. Применение ПИД регуляторов целесообразно, а зачастую и единственно возможно в процессах, где необходима высокая точность переходных процессов, непрерывный контроль и регулирование заданных параметров, недопустимы значительные колебания в системе.
Сравнение ПИД –регулятора с позиционным регулированием
В системах АСУ ТП наибольшее распространение получили два типа регуляторов – двухпозиционный и ПИД.
Двухпозиционный регулятор наиболее простой в использовании и широко распространенный.
Данный тип регулятора сравнивает значение входной величины с заданным параметром уставки. Если значение измеренной величины ниже заданного значения уставки, регулятор включает исполнительное устройство, при превышении заданного значения, исполнительное устройство выключается. Для предотвращения слишком частого срабатывания устройства, в следствии колебаний системы и следовательно изменении значений, задается минимальный и максимальный порог срабатывания — гистерезис, или по другому зона нечувствительности, мертвая зона, дифференциал. Например, нам необходимо поддерживать температуру в 15°С. Если гистерезис задан 2°, то регулятор будет включать нагрев при 14°С и отключать соответственно при 16°С.
Так или иначе, при таком типе регулирования происходят незатухающие колебания, частота и амплитуда которых зависит от параметров системы. Поэтому данный метод обеспечивает хороший результат в системах, обладающих инерционностью и малым запаздыванием. В частности, такой метод широко применяется при регулировании температуры в нагревательных печах.
В отличии от двухпозиционного с помощью ПИД-регулятора удается свести колебания системы к минимуму, благодаря тому, что при таком методе регулирования учитываются различные значения системы — фактическая величина, заданное значение, разность, скорость. Это позволяет стабилизировать систему и добиться повышения точности в десятки раз по сравнению с двухпозиционным методом. Конечно, здесь многое зависит от правильно подобранных коэффициентов ПИД регулятора.
Составляющие ПИД-регулятора
В стандартном ПИД-регуляторе есть три составляющие и каждая из них по своему воздействует на управление.
Пропорциональная — P (t) = Kp * e (t)
Учитывает величину рассогласования заданного значения и фактического. Чем больше отклонения значения, тем больше будет выходной сигнал, то есть пропорциональная составляющая пытается компенсировать эту разницу.
Однако пропорциональный регулятор не способен компенсировать полностью ошибку рассогласования. Всегда будет присутствовать так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. При увеличении коэффициента пропорциональности Kp статическая ошибка уменьшается, но могут возникнуть автоколебания и снижение устойчивости системы.
Интегральная – I (t) = Ki ∫e (t) dt
Интегральная составляющая используется для устранения статической ошибки. Она складывает значение предыдущих ошибок рассогласования и компенсирует их, можно сказать, что учится на предыдущих ошибках. То есть ошибка рассогласования умножается на коэффициент интегрирования и прибавляется к предыдущему значению интегрирующего звена. При выходе системы на заданный режим, интегральная составляющая перестает изменяться и не оказывает какого-либо серьезного воздействия на систему. Физически интегральная составляющая представляет задержку реакции регулятора на изменение величины рассогласования, внося в систему некоторую инерционность, что может быть полезно для управления объектами c большой чувствительностью.
Дифференциальная – D (t) = Kd de (t)/dt
Дифференциальная составляющая учитывает скорость изменения регулируемой величины, противодействуя предполагаемым отклонениям, вызванными возмущениями системы или запаздыванием. И чем больше будет величина отклоняться от заданной, тем сильнее будет противодействие, оказываемое дифференциальной составляющей. То есть она предугадывает поведение системы в будущем. При достижении величины рассогласования постоянного значения дифференциальная составляющая перестает оказывать воздействие на управляющий сигнал.
На практике какая-либо из составляющих может не использоваться (чаще всего Д-дифференциальная) и тогда мы получаем П-регулятор, ПИ-регулятор.
Методика настройки ПИД-регулятора
Выбор алгоритма управления и его настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.
В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.
В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.
Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип — проволочные, навитые на керамические трубки.
Требования: поддержание температуры по зонам печи +/- 5С.
МЕТОДИКА:
Настройка пропорциональной компоненты (Xp)
Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры;
∆t — период колебаний температуры.
Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.
3. Используя полученные параметры рассчитываем Ти и Тд.
| Зона пропорциональности | Коэффициент передачи | Постоянная времени интегрирования | Постоянная времени дифференцирования | |
| П-регулятор | 2*PBs | 0.5*Xp | ||
| ПИ-регулятор | 2.2*PBs | 0.45*Xp | 0.83*ʌТ | |
| ПИД-регулятор | 1.67*PBs | 0.6*Xp | 0.5*ʌТ | 0.125*ʌТ |
Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.
Вывод
Благодаря достаточно высоким получаемым результатам ПИД-регуляторы нашли широкое применение в системах автоматического управления.
При этом важно подчеркнуть, что настройка ПИД-регулятора является процессом довольно трудоемким и требует определенных знаний и индивидуального подхода для различных объектов управления.
ПИД-регуляторы – для чайников-практиков

Что мы делаем?
Итак, мы делаем регулятор холостого хода.
В данном случае однозначно просится к реализации система управления с обратной связью. В своей статье про «Датчики и АЦП» я рассказывал про систему управления с обратной связью, подробности ищите там. Также там была неплохая картинка на эту тему:
Что это будет в данном случае?
Мы хотим управлять оборотами двигателя в состоянии холостого хода. Для этого у нас есть шаговый двигатель, который открывает/закрывает заслонку для регулировки подачи воздуха. Также у нас есть таблица, которая указывает желаемую частоту двигателя в зависимости от текущей температуры. Управление объектом тут у нас выполняется шаговым двигателем. Состояние объекта определяется 1) оборотами двигателя и 2) текущей температурой.
Для данной картинки получаем следующее:
Что это за функция? Она выдает нам текущее значение шага, которое зависит от всего вышеперечисленного. Как она это делает?
Вся собака зарылась в том, что мы хотели на данный шаг получить одни обороты, а они в реальности совсем другие! Значит, нам нужно знать значение текущей ошибки (невязки), и она может быть вычислена как разность предполагаемых оборотов в будущем и текущих:
Ошибка (t) = Обороты (t+1) — Обороты (t).
В случае, когда обороты четко соответствуют требуемому значению (к чему мы и стремимся), ошибка будет равна нулю. Эта ошибка нам показывает насколько сильным должно быть воздействие.
Формула для следующего шага теперь может быть записана следующим образом:
Теперь можно вынести значение предыдущего шага за скобки:
Все понятно? Мы на каждом шаге работы регулятора должны задавать текущее положение шагового двигателя. Он зависит, понятное дело, от предыдущего шага и от ошибки. Шаговый двигатель управляется смещениями, поэтому нам не так уж и важен текущий шаг (проигнорируем тему выхода за пределы допустимого количества шагов – моему другу электрику это знать не обязательно). В итоге можно перейти к такой записи:
Формула ПИД-регулятора
Как я и обещал, формул тут не будет… ну, почти не будет. И этот раздел – как раз и будет формулой. Обещаю – больше формул не будет! Так что потерпите!
Итак, формула ПИД-регулятора: 
(навеяно Википедией)
Тут у нас следующие буковки (разъясним чуть ниже):
Вот это уже выглядит куда реальнее и понятнее! Мы вычисляем сумму трех составляющих. Каждая из них определяется своими коэффициентами. Если данный коэффициент нулевой, то составляющая в вычислении не участвует. С этой формулой мы и будем работать далее, ее я и реализую.
Впрочем, есть еще и другая, рекуррентная реализация:
Какая из них лучше/правильней? Математика, в общем-то, одинаковая. Коэффициенты тоже. Говорят, что есть разные подводные булыжники при реализации.
Обратите внимание! Коэффициенты тут – обязательно дробные числа! В языке программирования Си – как минимум float, а лучше бы и double.
Вся магия ПИД-регуляторов – именно в этих коэффициентах. Как их подбирать – посмотрим в конце. А сейчас переведем дух от математики и поедем к изучению поведения этой формулы.
Все расчеты и моделирование я проводил на модели в Excel. Он – файл – приложен внизу, с ним можно поиграться самостоятельно. Модель – сугубо для ознакомления с идеей! Т. е. не надо ее стараться привести к какому-то реальному процессу, искать в ней научный смысл и т. п. Там все цифры слегка «отфонарные». Но зато и файл простенький и несложный. И моделируется быстро. И дает возможность понять суть ПИД-регулятора. Пару слов по файлу я дам в конце.
Пропорциональная составляющая
Первый коэффициент – пропорциональный. Он самый очевидный и понятный (реально я когда-то давно сам вывел формулу ПИД-регулятора, кому-то показал, и он рассказал мне об этой теории; так вот, вывод я начал с пропорционального вида).
Рассмотрим его – пропорционального коэффициента — влияние на результат.

«Ожидаемое» – это то, что мы хотим получить. Вначале оно равно какому-то низкому значению (в нашем примере – это те обороты двигателя, которые создает стартер). Далее, в момент времени 3, оно вдруг стало равно 2000 (завели мотор и, исходя из текущей температуры, мы должны получить 2000 оборотов в минуту).
(Небольшая ремарка – в автомобилях частоту измеряют в кол-во оборотов в минуту!)
Сделаем первый вариант: Kp = 2. Посмотрим на красную линию. Что мы видим? По ходу дела обороты начали расти – ошибка стала снижаться – значение коррекции постепенно растет — красная линия растет (обороты двигателя увеличиваются). В какой-то момент (почему-то 13-ый) обороты достигают требуемой величины. Класс? Супер! Да вот только медленно как-то…
Попробуем другой коэффициент: Kp = 5. Что видим? Зеленая линия. Достигла результата шустро – на 6-ом шаге. Класс! Да вот – ой! – перелет (по науке перерегулирование). Потом, правда, вернулись назад – порядок.
А что если коэффициент сделать еще больше? Kp = 20. Синяя линия – бух! За один шаг! Но – сразу перелет. Потом падаем вниз – ошибка стала отрицательной. Опять сильно вниз! Рывок вверх! Опять вниз! Что видим? Пошли колебания. Они, слава Богу, затухающие.
Если увеличивать коэффициент больше, то такие колебания могут стать незатухающими. Система начнет колебаться все больше и больше, пока не … ну-у, тут уже все зависит от конкретной системы.
Какова природа колебаний? Система, на которую воздействуют, всегда (в реальной жизни) инерционна. Обороты повышаются – коэффициент падает к нулю. И вот – достигли нужной точки. Коэффициент ошибки (и регулирования) достиг нуля. Но ведь процесс поднятия оборотов инерционен! Движёк раскочегарен, обороты продолжают по инерции расти. И тогда будем двигать заслону назад – опускать обороты. Опять достигли нуля – а обороты продолжают падать… И так, в общем-то, до бесконечности.
Особенно это очевидно в системах поддержания температуры. Нагрев надо выключать до нужной температуры – чтобы сам нагреватель перестал разогреваться и греть объект.
Для решения этой проблемы используется следующая –
Интегральная составляющая
Эта составляющая накапливает ошибку (как и любой интегратор). Т. е. постепенно накапливается эта самая ошибка, интегратор «наполняется» и его воздействие увеличивается. Эффект от такого накопления не мгновенен — ибо ошибка должна накопиться, на что уходит некоторое количество шагов алгоритма.
Рассмотрим случай, когда Kp = 5, а Ki будем менять:
Дифференциальная составляющая
Реакция на помехи
Надо еще не забывать об одной такой малоприятной вещи – о помехах. Они будут раскачивать лодку нашей системы.
Вот картинка, когда у нас стоит задача поддерживать одно и то же значение оборотов: 
Шумовое (случайное) воздействие – одинаковое для всех вариантов.
Вариант 1 (красный) – Kp = 10, Ki = 0, Kd = 10.
Вариант 2 (зеленый) – Kp = 10, Ki = 2, Kd = 0.
Вариант 3 (синий) – Kp = 10, Ki = 2, Kd = 6.
Как видно, с добавлением составляющих стабильность (немного) увеличивается.
Настройка
Я думаю, общее представление о формуле ПИД-регулирования вы получили. Программируется легко, эффект красивый. И следующий вопрос у вас будет – «а как получит коэффициенты»? И вот тут все становится кисло… Потому что, если до этих пор шла строгая математика, то дальше начинаются танцы с бубнами, шаманство и шайтанство. Нет, все-таки есть какие-то точные методы, но мне становится плохо при мысли, что я должен это проделать для своего двигателя в автомобиле!
В комментариях мой метод (и мое понимание) настройки разгромили, закопали и затоптали. И порекомендовали прочитать хорошую книгу «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДЛЯ «ЧАЙНИКОВ»» К.Ю. Полякова (созвучное название, не находите?). Согласен, тема (настройки) сложная, для меня неоднозначная, поэтому соглашусь с комментирующими — надо прочитать эту книгу и глубже вникать в тему. Но… это уже будет не для уровня чайников, не так ли? В книге Полякова формул более чем достаточно, а это уже уровень электро-чайника! Так что позвольте мне изложить свой подход. Неидеальный, но достаточный для старта и более детального изучения темы.
Частота опроса/воздействия
Есть очень важный момент работы при разработке ПИД-регулятора: воздействие должно быть строго периодичным, т. е. производиться через равные промежутки времени! Аналогично, ошибка должна вычисляться также периодически.
Какой должен быть период измерений/воздействий? Для начала определите время стабилизации системы – за сколько должно быть достигнуто устойчивое состояние (в случае регулятора холостого хода хватит периода 0.5 секунды). Потом разделите это время на 10 … 100 – и вы получите длительность шага (в моем случае хватит и 10 мсек). А вообще – чем выше частота, тем лучше! Но надо помнить, что операции с дробными числами весьма медленны. Фактически, они и зададут вам период работы.
Посмотрим, как период опроса (и воздействия) влияет на качество результата:
Коэффициенты ПИД-регулятора: – Kp = 10, Ki = 0, Kd = 0.
Вариант 1 (красный) – период опроса 0.5 у.е.
Вариант 2 (зеленый) – период опроса 0.35 у.е.
Вариант 3 (синий) – период опроса 0.15 у.е.
Как видим, в первом случае есть мощные выбросы. Во втором случае (70% от первого периода) они стали слабее, а в третьем (30%) – преобразование вообще получилось гладким! Т. е. для первых двух вариантов нужны дополнительно интегральная или дифференциальная составляющие, а для последнего мы обошлись только пропорциональной. А это существенная разница в вычислениях!
Так что вопросу выбора периода надо уделить первостепенное внимание.
Итак, время выбрали, все коэффициенты сбросили в ноль. Начинаем управлять системой.
Идеально, если вы сможете собрать статистику – записывать воздействие/результат/сопутствующую информацию в текстовый файл. Потом его можно открыть в том же Excel и проанализировать.
Настройка пропорционального коэффициента Kp
Для начала я устанавливаю коэффициент Kp в 1 и смотрю, что будет. Растет слишком медленно – увеличиваю. В какой-то момент начнутся перелеты и колебания. Значит, многовато – уменьшаем. Исчезли – немного увеличиваем. Начались – немного уменьшаем. Исчезли — … И так далее, пока не надоест. В итоге получили достаточно устойчивый пропорциональный регулятор, который надо немного скорректировать (надо ли? Если все работает вполне качественно, то не морочим себе голову и считаем, что все настроено)
Настройка дифференциального коэффициента Kd
Понемногу наращиваю коэффициент Kd — 0.5, 1,… Колебания системы уменьшаются, все работает красивее… Пока не происходит обратное – начинаются мощные выбросы. Все, перерегулировали, уменьшаем.
Итак, имеем выбросы – уже меньше, но все равно имеем. Самое то сгладить, притормозить воздействие!
Настройка интегрально го коэффициента Ki
Шаманим дальше. Берем совсем немного – 0.1 для начала. Можно попробовать и небольшое отрицательное значение. Смотрим, пробуем, крутим…
Процесс этот – настройки – итерационный. Стоит пробовать разные варианты, начинать сначала. Для меня он по-прежнему туманен и шайтанен.
Дополнительные модули?
Построили, сделали — и увидели, что все равно есть какие-то биения, ненужные колебания. Ну-с, а что вы хотели. Серьезный подход изобилует формулами, сложными расчетами!
И Бог с ними — вот что я скажу! Можно вполне на выходе добавить усреднение нескольких последних тактов — дешево (в плане расчетов) и сердито (в плане стабильности воздействий). Можно поставить еще какие-нибудь фильтры.
Не будем догматичными! Кто сказал, что нужно ограничиться одним лишь ПИД-регулятором?
Информация по модели
А теперь – обещанная пара слов по Excel-файлу. В нем реализована модель, схожая с перемещением по линии. Не очень корректная, возможно, но вполне достаточная для старта (может, по результатам обсуждения сделаю более точную модель — возьму для примера модель электродвигателя из статьи Полякова). Есть предыдущее положение, скорость и ускорение. Скорость рассчитывается как разница предыдущих перемещений. Ускорение определяется как П-И-Д – воздействие, умноженное на коэффициент усиления (в верхней части таблицы).
В таблице представлены 3 варианта. Они настраиваются сверху:
В заключение – о реализации
Как видите – ничего революционного!
Прежде всего, все радости происходят в отдельной функции, которая вызывается периодически.
Первый вызов – инициализация из EEPROM или откуда-нибудь еще коэффициенты, обнуляем переменные для рекурсивных вызовов. Потом начинаем пошагово 1) измерять, 2) вычислять, 3) воздействовать, и так по кругу. Заодно производится привязка к реальному времени. Если текущее время меньше требуемого (функция TimeIsLower), то действие не производится.
В комментариях поинтересовались — зачем такие сложности с машиной состояний? С недетерминированным алгоритмом? Отвечаю: благодаря такому подходу я реализую простенький «параллелизм». Т. е. в промежутке между этапами вычислений я делаю какие-то другие действия (в моем случае общение по UART, которое может быть весьма напряженным — когда я использую сий девайс как логгер событий).
Вроде бы все… Что забыл, что перепутал – пишите. Как всегда, приветствуются комментарии о ляпах и ошибках!
P. S.Хочу поучаствовать в конкурсе, поэтому добавляю:






