Что такое вписанная и описанная окружность
Что такое вписанная и описанная окружность
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
Окружность, вписанная в прямоугольный треугольник
Окружность, описанная около прямоугольного треугольника
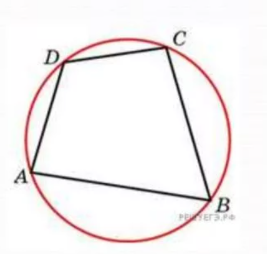
Четырехугольник, вписанный в окружность
Окружность, вписанная в ромб
Что такое вписанная и описанная окружность
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
Окружность, вписанная в прямоугольный треугольник
Окружность, описанная около прямоугольного треугольника
Четырехугольник, вписанный в окружность
Окружность, вписанная в ромб
Вписанная и описанная окружности
Вы будете перенаправлены на Автор24
Вписанная окружность
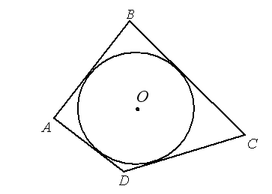
Если все стороны многоугольника являются касательными одной окружности, то такая окружность называется вписанной в многоугольник (рис 1).
Многоугольник, удовлетворяющий условию определения 1, называется описанным около окружности.
Рисунок 1. Вписанная окружность
Теорема 1 (об окружности, вписанной в треугольник)
В любой треугольник можно вписать окружность и притом только одну.
Доказательство.
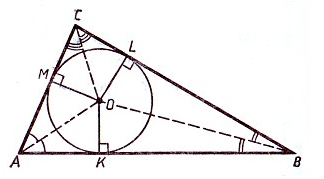
Рисунок 2. Иллюстрация теоремы 1
Готовые работы на аналогичную тему
Теорема доказана.
Следствие 1: Центр вписанной в треугольник окружности лежит в точке пересечения его биссектрис.
Приведем еще несколько фактов, связанных с понятием вписанной окружности:
Не во всякий четырехугольник можно вписать окружность.
В любом описанном четырехугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Описанная окружность
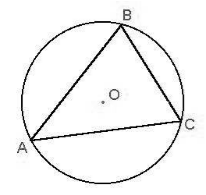
Если на окружности лежат все вершины многоугольника, то окружность называется описанной около многоугольника (Рис. 3).
Многоугольник, удовлетворяющий условию определения 2, называется вписанным в окружность.
Рисунок 3. Описанная окружность
Теорема 2 (об окружности, описанной около треугольника)
Около любого треугольника можно описать окружность и притом только одну.
Доказательство.
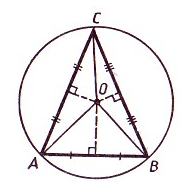
Рисунок 4. Иллюстрация теоремы 2
Теорема доказана.
Следствие 1: Центр описанной около треугольника окружности совпадает с точкой пересечения его серединных перпендикуляров.
Приведем еще несколько фактов, связанных с понятием описанной окружности:
Около четырехугольника не всегда можно описать окружность.
Пример задачи на понятия вписанной и описанной окружности
В равнобедренном треугольнике основание равно 8 см, боковая сторона равна 5 см. Найти радиус вписанной окружности.
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 03 2021
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Описанная окружность
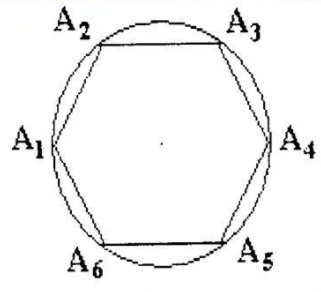
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.
Вписанная окружность
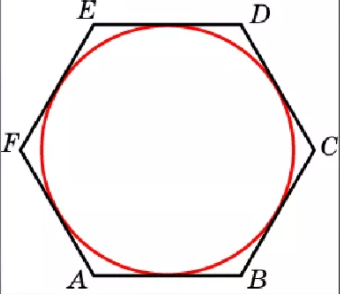
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.
Вписанный и описанный треугольники
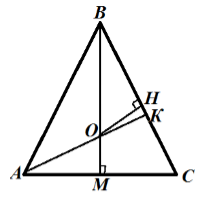
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
В любой треугольник можно вписать окружность: 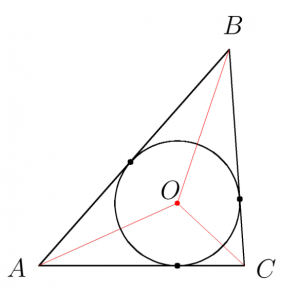
Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Вписанный и описанный четырехугольники
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.
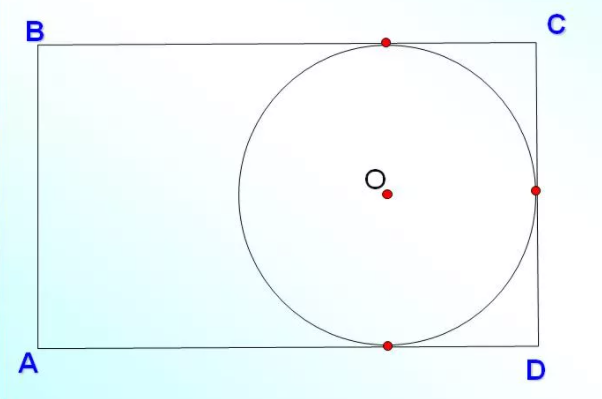
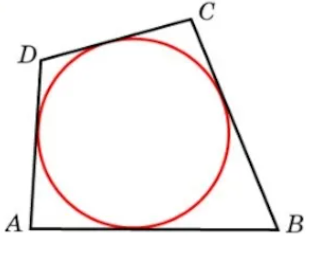
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.
На рисунке выполняется данное условие, то есть AD + BC=DC + AB
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.
На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.
Что такое вписанная и описанная окружность
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
Окружность, вписанная в прямоугольный треугольник
Окружность, описанная около прямоугольного треугольника
Четырехугольник, вписанный в окружность
Окружность, вписанная в ромб