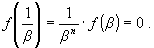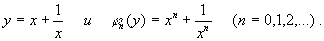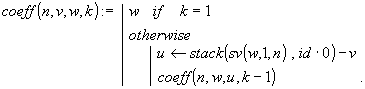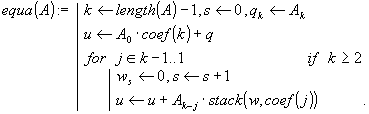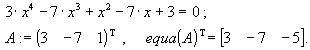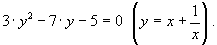Что такое возвратное уравнение

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.

Источник

ВОЗВРАТНОЕ УРАВНЕНИЕ

в к-ром коэффициенты, равноудаленные от начала и конца, равны между собой:

В. у. степени 2nможно привести к уравнению га-й степени, положив 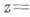БСЭ-З

Смотреть что такое «ВОЗВРАТНОЕ УРАВНЕНИЕ» в других словарях:

возвратное уравнение — grįžtamumo lygtis statusas T sritis fizika atitikmenys: angl. reciprocal equation vok. reziproke Gleichung, f; Reziprokgleichung, f rus. возвратное уравнение, n pranc. équation réciproque, f … Fizikos terminų žodynas

Возвратное уравнение — уравнение вида: a0 xn + a1 xn 1 +. + an 1 х + an = 0, в котором коэффициенты, равноудалённые от начала и конца, равны между собой: ai = an i. Таково, например, уравнение 2×5 5×4 + x3 + x2 5x + 2 = 0. В. у. степени 2n можно привести к… … Большая советская энциклопедия

Уравнение четвёртой степени — График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия

Квадратное Уравнение — Квадратное уравнение уравнение вида ax2 + bx + c = 0, где Содержание 1 Уравнение с вещественными коэффициентами … Википедия

Источник

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Для решения этого типа уравнений применяются формулы сокращенного умножения:

Остается лишь найти корни квадратных трехчленов.

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

Теперь найдем корни квадратных трехчленов.

Мы получили четыре комплексных корня.

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Решим полученное квадратное уравнение:

Решим первое уравнение:

Решим второе уравнение:

Решение биквадратного уравнения

Решение

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Решение

Источник

Решение возвратных уравнений (урок).

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Решение возвратных целых уравнений с помощью введения новой переменной.

Урок изучения нового материала.

Цели: рассмотреть один из видов целых уравнений – возвратные уравнения 4 степени, научиться их решать; совершенствовать навык решения целых уравнений, в том числе, методом введения новой переменной, подготовка к экзамену.

Актуализация знаний: решение заданий из открытого банка заданий ОГЭ.

3. Ответ: 4

4. Ответ: х

6. Ответ:

Изучение нового материала: Возвратные уравнения 4 степени, это уравнения вида:

2.Сгруппировать слагаемые (первый с последним, второй с четвёртым).

Привести уравнение к виду а + с = 0

3. Ввести новую переменную t = , тогда выполнено t 2 = , т.е. = t 2 – 2.

4. Выполнить подстановку и решить квадратное уравнение.

5.Вернуться к замене и решить получившиеся уравнения.

Закрепление материала: Решение заданий: 7. Ответ: 0,5; 2.

Подведение итогов. Выставление отметок. Домашнее задание: п. 16, № 350, 373 а), 370 а).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-947123

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования

Время чтения: 2 минуты

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Что такое возвратное уравнение

Рассмотрим две задачи, относящиеся к возвратным уравнениям. Начнем с определения.

называется возвратным (или возвратным первого рода), если a₀ ¹ 0 и коэффициенты членов левой части (20), равноотстоящие от концов, равны между собой. Левую часть (20) называют возвратным многочленом. Записать его можно так:

В дальнейшем нам будут полезны следующие простейшие свойства возвратных уравнений.

	Возвратное уравнение не имеет корней, равных нулю (a0 ¹ 0).
	Если b есть корень (20), то 1/ b также является корнем (20). В самом деле:

Частное от деления многочлена f(x ) нечетной степени на x +1 снова является возвратным многочленом (доказывается по индукции).

Последнее свойство сводит вопрос о решении любых возвратных уравнений к решению возвратных уравнений лишь четной степени:

Но для (21) можно записать равносильное уравнение:

(22)

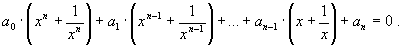
Далее, если положить y=x+1/x и учесть “символьную рекуррентность”:

(23)

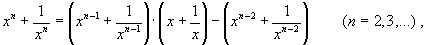
то индукцией по n доказывается, что левая часть (20) выражается через y в виде некоторого многочлена j _n (y) степени n.

адача 47. Пусть

Решение. Из определения j _n (y) и соотношений (23) вытекает, что

(24)

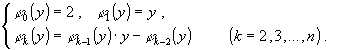
Обозначим через a (k) (k=0, 1, …, n ) векторы коэффициентов многочленов j _k(y) и дополним их до длины n +1 начальными нулевыми компонентами. Тогда

При обращении к функции equa(A ) в качестве фактического параметра должен передаваться вектор с компонентами, представляющими собой первые n +1 последовательных коэффициентов исходного возвратного уравнения.

Иными словами, получили уравнение:

Источник