Что такое восьмибитная двоичная запись числа

Двоичная система счисления. Бит и байт. Сегментация памяти.

Рассмотрим, как в памяти компьютера хранятся данные.

нуль будет обозначаться как 0000 (четыре нуля),

(т.е. правую единицу заменяем на 0 и вторую устанавливаем в 1).

Рис. 1. Один байт с кодом буквы Z

(буквы н и р обозначают: намагничено или размагничено соответственно)

Можно элементарно проверить. Создайте в текстовом редакторе файл с любым именем и запишите в нем один символ, например, «М» (но не нажимайте Enter!). Если вы посмотрите его размер, то файл будет равен 1 байту. Если ваш редактор позволяет смотреть файлы в шестнадцатеричном формате, то вы сможете узнать и код сохраненного вами символа. В данном случае буква «М» имеет код 4Dh в шестнадцатеричной системе, которую мы уже знаем или 1001101 в двоичной.

Т.о. в регистры можно загружать двоичные, десятичные и шестнадцатеричные числа.

В результате в регистрах AX, BH и CL будет находится одно и тоже число, только загружаем мы его в разных системах. Компьютер же будет хранить его в двоичном формате (как в регистре BH).

Как перевести двоичное число в десятичное:

Надо сложить двойки в степенях, соответствующих позициям, где в двоичном стоят единицы. Например:

Возьмем число 20. В двоичной системе оно имеет следующий вид: 10100b

Итак (начнем слева направо, считая от 4 до 0; число в нулевой степени всегда равно единице (вспоминаем школьную программу по математике)):

Как перевести десятичное число в двоичное:

Можно делить его на два, записывая остаток справа налево:

В результате получаем: 10100b = 20

Как перевести шестнадцатеричное число в десятичное:

В шестнадцатеричной системе номер позиции цифры в числе соответствует степени, в которую надо возвести число 16:

В настоящий момент есть множество калькуляторов, которые могут считать и переводить числа в разных системах счисления. Например, калькулятор Windows, который должен быть в инженерном виде. Очень удобен калькулятор и в DOS Navigator’е. Если у вас есть он, то отпадает необходимость в ручном переводе одной системы в другую, что, естественно, упростит вам работу. Однако, знать этот принцип крайне важно!

Сегментация памяти в DOS.

Возьмем следующее предложение: «Изучаем сегменты памяти». Теперь давайте посчитаем, на каком месте стоит буква «ы» в слове «сегменты» от начала предложения включая пробелы. На шестнадцатом. Подчеркну, что мы считали слово от начала предложения.

Теперь немного усложним задачу и разобьем предложение следующим образом (символом «_» обозначен пробел):

В слове «Изучаем» символ «И» стоит на нулевом месте; символ «з» на первом, «у» на втором и т.д. В данном случае мы считаем буквы начиная с нулевой позиции, используя два числа. Назовем их сегмент и смещение. Тогда, символ «ч» будет иметь следующий адрес: 0000:0003, т.е. сегмент 0000, смещение 0003. Проверьте.

В слове «память» считаем буквы начиная с 0020 сегмента и также с нулевой позиции. Т.о. символ «а» будет иметь аодрес 0020:0001, т.е. сегмент 0020, смещение 0001. Опять проверим.

Итак, мы выяснили, что для того, чтобы найти адрес нужного символа необходимо два числа: сегмент и смещение внутри этого сегмента. В Ассемблере сегменты хранятся в сегментных регистрах: CS, DS, ES, SS (см. предыдущий выпуск ), а смещения могут храниться в других (но не во всех).

Регистр ES дополнительный сегментный регистр, который может хранить любой другой сегмент (например, сегмент видеобуфера).

Пример N 2:

Давайте попробуем загрузить в пару регистров ES:DI сегмент и смещение буквы «м» в слове «памяти» из примера N 1 (см. выше). Вот как это запишется на Ассемблере:

Теперь в регистре ES находится сегмент с номером 20, а регистре DI смещение к букве «м» в слове «памяти». Проверьте, пожалуйста.

Здесь стоит отметить, что загрузка числа (т.е. какого-нибудь сегмента) напрямую в сегментый регистр запрещена. Поэтому мы в строке (1) загрузили сегмент в AX, а в строке (2) загрузили в регистр ES число 20, которое находилось в регистре AX:

Когда мы загружаем программу в память, она автоматически располагается в первом свободном сегменте. В файлах типа *.com все сегментные регистры автоматически инициализируются для этого сегмента (устанавливаются значения равные тому сегменту, в который загружена программа). Это можно проверить при помощи отладчика. Если, например, мы загружаем программу типа *.com в память, и компьютер находит первый свободный сегмент с номером 5674h, то сегментные регистры будут иметь следующие значения:

Код программы типа *.com должны начинаться со смещения 100h. Для этого мы, собственно, и ставили в наших прошлых примерах программ оператор org 100h, указывая Ассемблеру при ассемблировании использовать смещение 100h от начала сегмента, в который загружена наша программа (позже мы рассмотрим для чего это нужно). Сегментные же регистры, как я уже говорил, автоматически принимают значение того сегмента, в который загрузилась наша программа.

Пара регистров CS:IP задает текущий адрес кода. Теперь рассмотрим, как все это происходит на конкретном примере:

Пример N 3.

Строка (2) сообщает, что код программы (как и смещения внутри сегмента CSEG) необходимо отсчитывать с 100h. По этому адресу в память всегда загружаются программы типа *.com.

Запускаем программу из Примера N 3 в отладчике. Допустим, она загрузилась в свободный сегмент 1234h. Первая команда в строке (4) будет располагаться по такому адресу:

1234h:0100h (т.е. CS = 1234h, а IP = 0100h) (посмотрите в отладчике на регистры CS и IP).

Перейдем к следующей команде (в отладчике CodeView нажмите клавишу F8, в другом посмотрите какая клавиша нужна; будет написано что-то вроде «F8-Step»). Теперь вы видите, что изменились следующие регистры:

AX = 0900h (точнее, AH = 09h, а AL = 0, т.к. мы загрузили командой mov ah,9 число 9 в регистр AH, при этом не трогая AL. Если бы AL был равен, скажем, 15h, то после выполнения данной команды AX бы равнялся 0915h)

Обратите внимание, что в Ассемблере мы пишем:

а в отладчике видим следующее:

Почему так происходит? Дело в том, что при ассемблировании программы, Ассемблер подставляет вместо offset My_name реальный адрес строки с именем My_name в памяти. Можно, конечно, записать сразу

Программа будет работать нормально. Но для этого нам нужно высчитать самим этот адрес. Попробуйте вставить следующие команды, начиная со строки (7) в примере N 3:

Просто продублируем команду int 20h (хотя, как вы уже знаете, до строки (8) программа не дойдет).

Теперь ассемблируйте программу заново. Запускайте ее под отладчиком. Вы увидите, что в DX загружается не 109h, а другое число. Подумайте, почему так происходит. Это просто!

В окне «Memory» («Память») вы должны увидеть примерно такое:

Но вернемся. Итак, мы загрузили в DX адрес строки в сегменте, который мы назвали CSEG (строки (1) и (9) в Прмере N 3). Теперь переходим к следующей команде: int 21h. Вызываем прерывание DOS с функцией 9 (mov ah,9) и адресом строки в DX (mov dx,offset My_name).

Как я уже говорил раньше, для использования прерываний в программах, в AH заносится номер функции. Номера функций нужно запоминать.

Наше первое прерывание.

Функция 09h прерывания 21h выводит строку на экран, адрес которой указан в регистре DX.

Изобразим это в таблице (так всегда теперь будем делать):

Вход: AH = 09h, DX = адрес ASCII-строки символов, заканчивающийся ‘$’

Вот мы и рассмотрели сегментацию памяти. Если я что-то упустил, то это рассмотрим в последующих выпусках. Очень надеюсь на то, что вы разобрались в данной теме.

Теперь интересная программка для практики, которая выводит в верхний левый угол экрана веселую рожицу на синем фоне:

Многие операторы вы уже знаете. Поэтому я буду объяснять только новые.

В данном примере мы используем вывод символа прямым отображением в видеобуфер.

Можете поэксперементировать с данным примером. Только не меняйте строки (4) и (5). Сегментный регистр должен быть ES (можно, конечно, и DS, но тогда надо быть осторожным). Более подробно данный метод рассмотрим позже. Сейчас нам из него нужно понять принцип сегментации на практике.

Источник

Обучение : Программирование на Ассемблере для PIC

Системы счисления

В регистр может быть записано одно положительное число от 0 до 255. Машинная математика, в т.ч. и математика МК, не может оперировать десятичными числами, для этого используется так называемая двоичная система счисления (или иначе – бинарная).

Десятичное число 255 в двоичной системе выглядит как «11111111», т.е. восемь единиц, а двоичное число «0» – как восемь нулей «00000000». Следует заметить, что обозначение нуля одним символом «0», в любой системе счисления равно нулю. Таким образом, «регистр» необходимо рассмотреть детальнее, т.к. в него записывается не десятичное число, а двоичное.

Запомните: «мы говорим о десятичных числах в МК, а подразумеваем двоичные». Ниже рисунок памяти в реальности

Такие двоичные числа называют восьмибитными числами или байт.

Запомните: 1 БАЙТ = 8 БИТ.

Нумерация битов идёт справа налево от нуля до семи. В нашем примере нулевой бит равен нулю, а седьмой бит равен единице. Это так называемая бинарная система счисления, где используются две цифры «0» и «1». Перебирая нули и единицы в байте, мы можем получить 255 комбинаций, т.е. любое число на интервале от 0 до 255. Таким образом, в регистр мы можем записать десятичное число от 0 до 255.

Необходимо понять, что в регистр физически записывается число в восьмибитном представлении, работу регистра проще представить как набор из 8-ми крошечных выключателей, каждый из которых может быть включен или выключен.

О сайте.
Электронные устройства и модели,
обучение и консультация,
документация и средства разработки.
Принимаем на реализацию проекты,
услуги, идеи. Возмездная помощь.

Здесь может быть
ваша реклама

Понравилась конструкция,
но не можете собрать?
Обращайтесь, мы удовлетворим
ваши запросы и пожелания!
Напишите нам письмо.

Источник

Битовое представление чисел

Так как на уровне схем почти вся логика бинарная, ровно такое представление и используется для хранения чисел в компьютерах: каждая целочисленная переменная указывает на какую-то ячейку из 8 ( char ), 16 ( short ), 32 ( int ) или 64 ( long long ) бит.

Эндианность

Единственная неоднозначность в таком формате возникает с порядком хранения битов — также называемый эндианностью. Зависимости от архитектуры он может быть разным:

Хотя big-endian более естественный для понимания — на бумаге мы ровно так обычно и записываем бинарные числа — по разным причинам на большинстве современных процессоров по умолчанию используется little endian.

Иными словами, «$i$-тый бит» означает «$i$-тый младший» или «$i$-тый справа», но на бумаге мы ничего не инвертируем и записываем двоичные числа стандартным образом.

Битовые операции

Помимо арифметических операций, с числами можно делать и битовые, которые интерпретируют их просто как последовательность битов.

Сдвиги

Битовую запись числа можно «сдвигать» влево ( x ) или вправо ( x >> y ), что эквивалентно умножению или делению на степень двойки с округлением вниз.

Обычное умножение и деление — не самые быстрые операции, однако все битовые сдвиги всегда работают ровно за один такт. Как следствие, умножение и деление на какую-то фиксированную степень двойки всегда работает быстро — даже если вы не используете сдвиги явно, компилятор скорее всего будет проводить подобную оптимизацию.

Побитовые операции

Все побитовые операции тоже работают за один такт, вне зависимости от типа данных. Для больших не вмещающихся в один регистр битовых последовательностей существует битсет.

Маски

Битовые операции таким образом часто используются операций над множествами, представляемыми битовыми мазками — например, в задачах на полный перебор или динамическое программирование.

Выделить i-й бит числа

Напомним, что нумерация идет с младших бит и начинается с нуля.

Получить число, состоящее из k единиц

Инвертировать все биты числа

Добавить i-й элемент в множество

Удалить i-й элемент из множества, если он есть

Также добавляет этот элемент, если его нет.

Знаковые числа

Целочисленные переменные делятся на два типа — знаковые (signed) и беззнаковые (unsigned).

Упражнение. Каких чисел больше: положительных или отрицательных?

Осторожно. В стандарте C/C++ прописано, что переполнение знаковых переменных приводит к undefined behavior, поэтому полагаться на описанную логику переполнения нельзя, хотя равно это скорее всего и произойдет.

128-битные числа

Общих регистров размера больше 64 в процессорах нет, однако умножение и несколько смежных инструкций могут использовать два последовательных регистра как один большой. Это позволяет быстро перемножать два 64-битных числа и получать 128-битный результат, разделенный на нижние биты и верхние.

Это весьма специфичная операция, и поэтому в языках программирования нет полноценной поддержки 128-битных переменных. В C++ однако есть «костыль» — тип __int128_t — который фактически просто оборачивает пару из двух 64-битных регистров и поддерживает арифметические операции с ними.

Базовые арифметические операции с ним чуть медленнее, его нельзя напрямую печатать, и деление и прочие сложные операции будут вызывать отдельную библиотеку и поэтому работать очень долго, однако в некоторых ситуациях он оказывается очень полезен.

Источник

Бит | Байт | Системы счисления

Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.

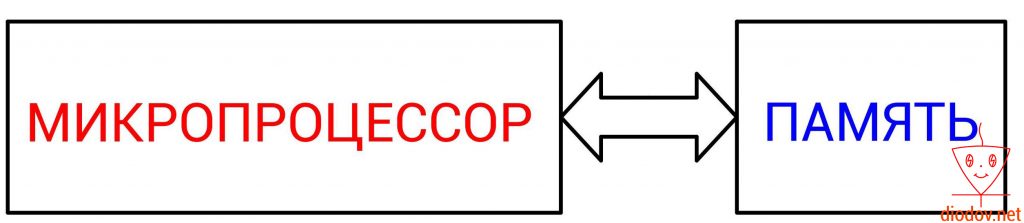
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.

Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.

Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.

Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.

Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.

Десятичная система счисления

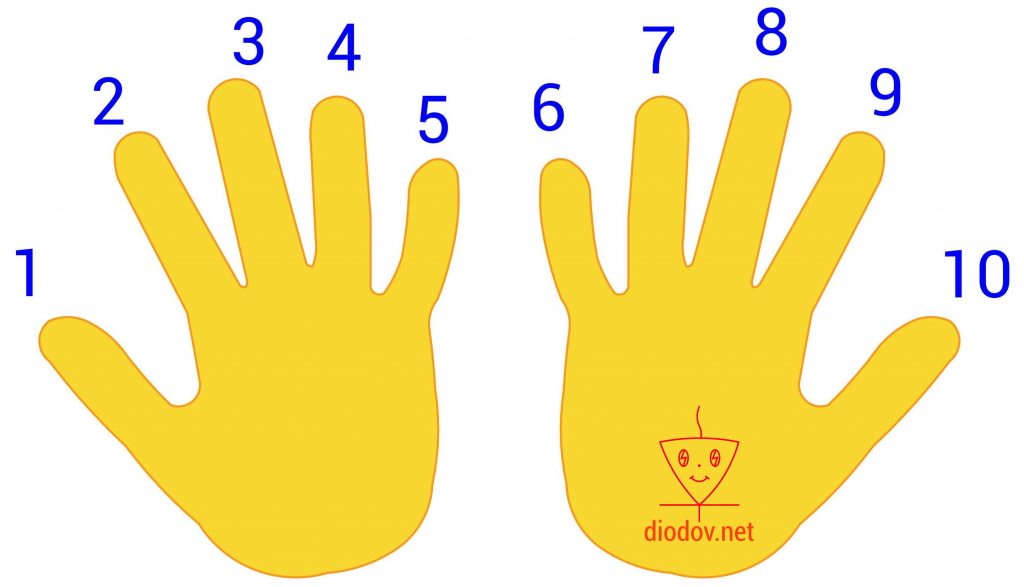
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.

Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.

Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.

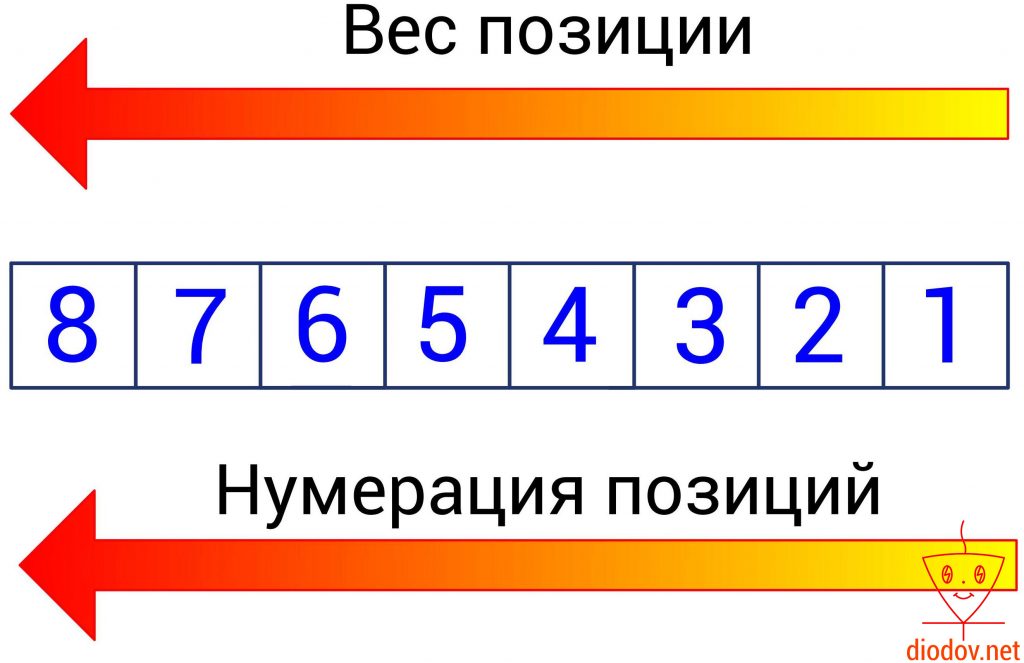
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.

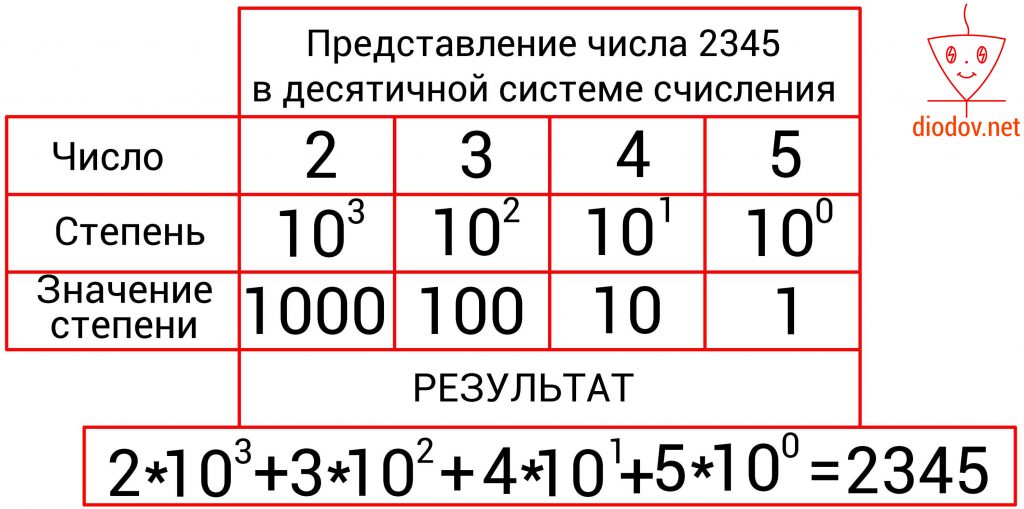
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.

Двоичная система счисления

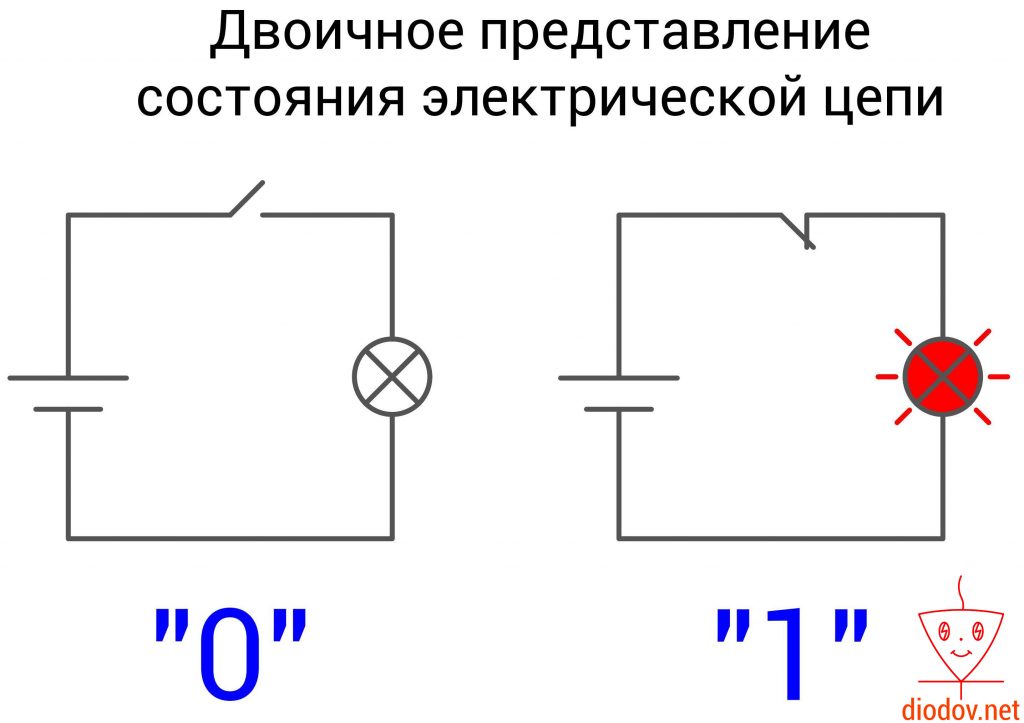
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.

Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.

Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:

1101₁₀ – десятичное.

При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.

0b11010101 – двоичное;

11010101 – десятичное.

Бит и байт

Двоичная система счисления также используется при хранении и обработке информации.

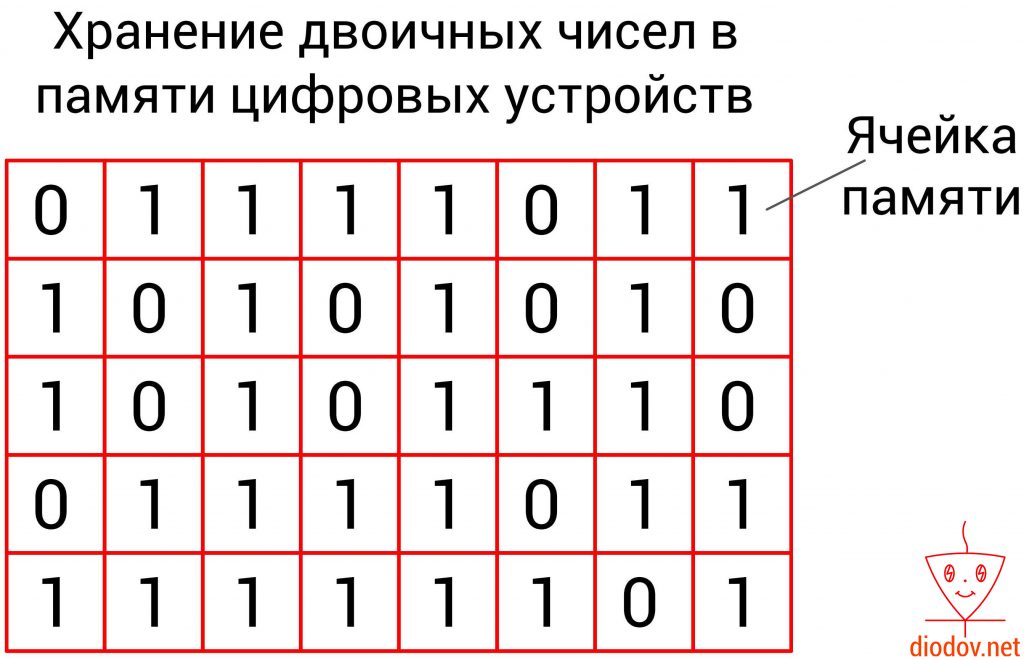
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.

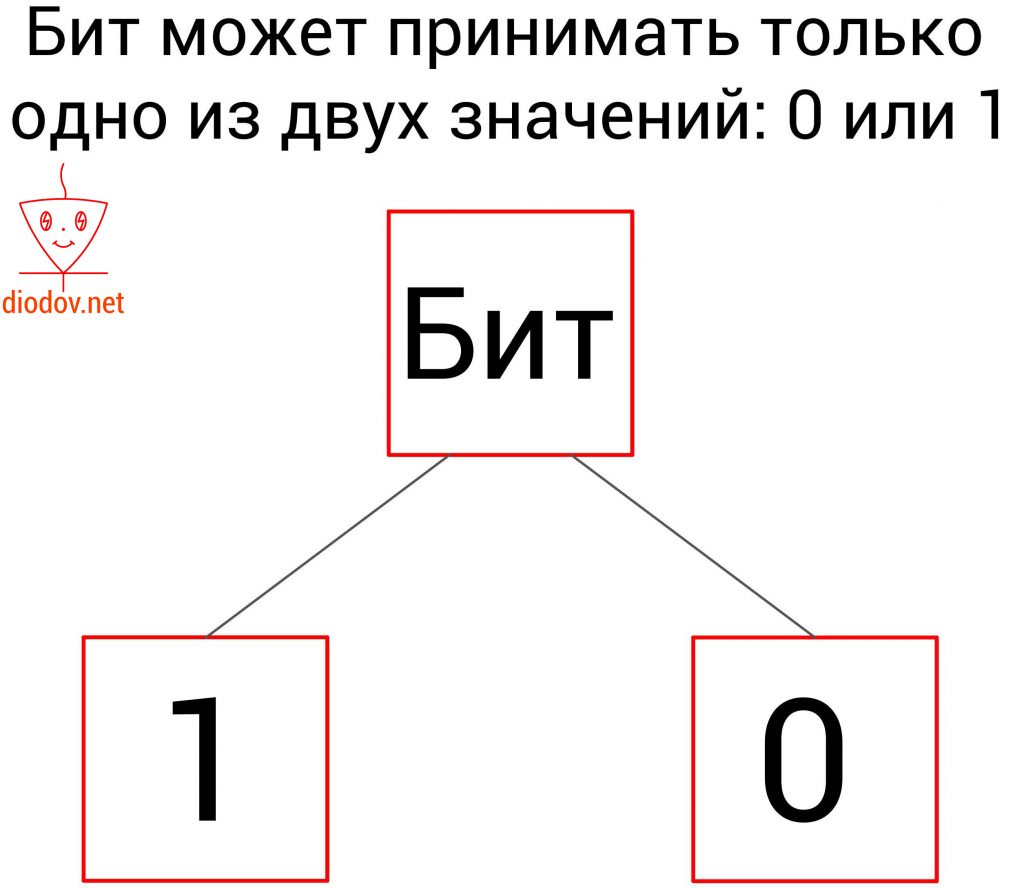
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.

Bit происходит от двух английских слов Binary Digit (двоичное число).

При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.

Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.

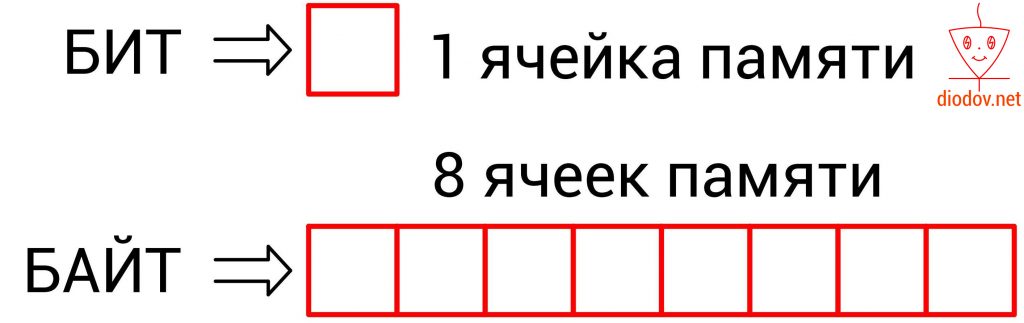
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.

1 байт = 8 бит

В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.

На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.

1 килобайт (кБ) = 1024 байт

1 мегабайт (МБ) = 1024 кБ

1 гигабайт (ГБ) = 1024 МБ

1 терабайт (ТБ) = 1024 ГБ

Преобразование десятичного числа в двоичное

На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.

Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.

Теперь давайте переведем число 125 в двоичную форму.

125/2 = 62 остаток 1

Получаем двоичное число 1111101₂

Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.

Второй способ

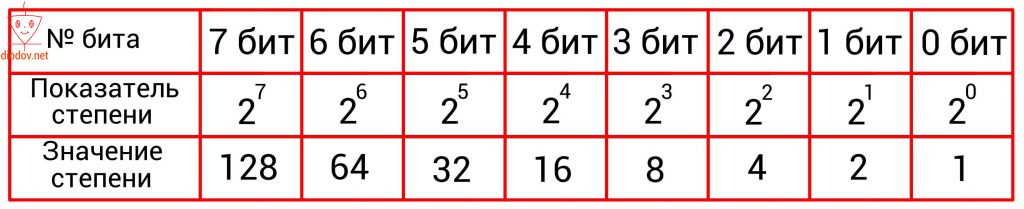
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.

Давайте преобразуем 125.

Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.

Преобразование двоичного числа в десятичное

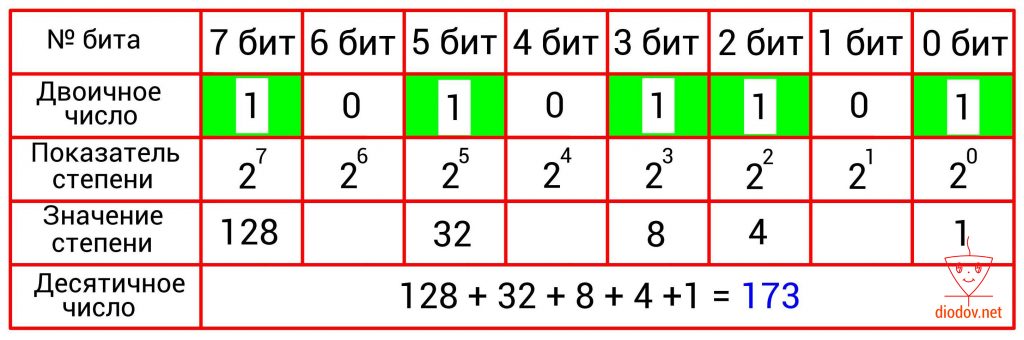
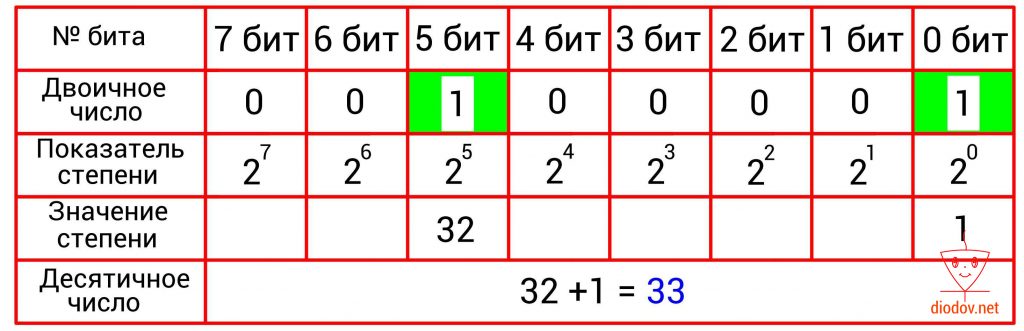
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.

В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.

Шестнадцатеричная система счисления

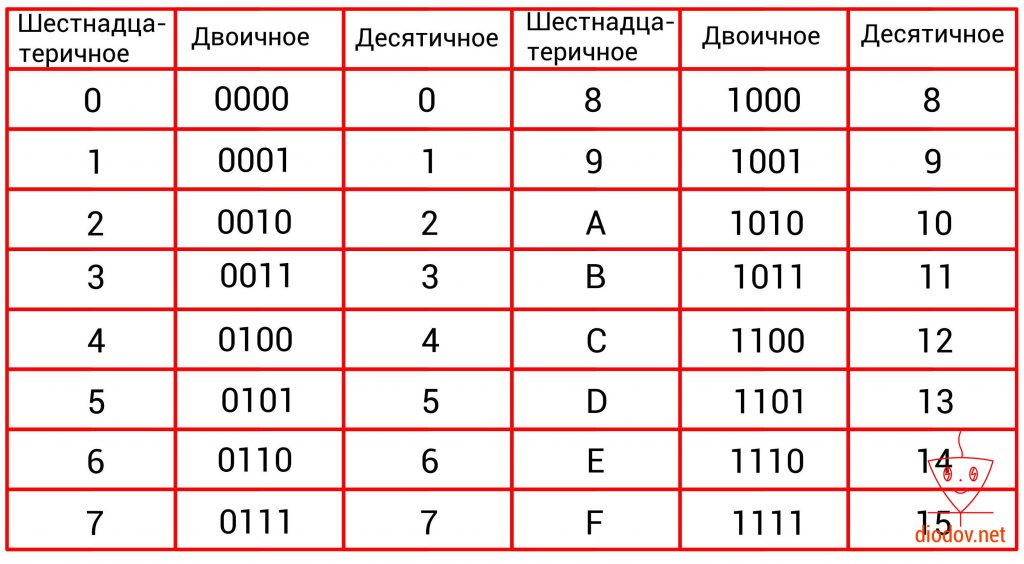
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 100₁₀ или 7 двоичных разрядов 1100100₂ и только 2 шестнадцатеричных разряда 64₁₆.

А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:

1 000 000₁₀ = 1111 0100 0010 0100 0000₂ = F4240₁₆

Преобразование двоичного числа в шестнадцатеричное

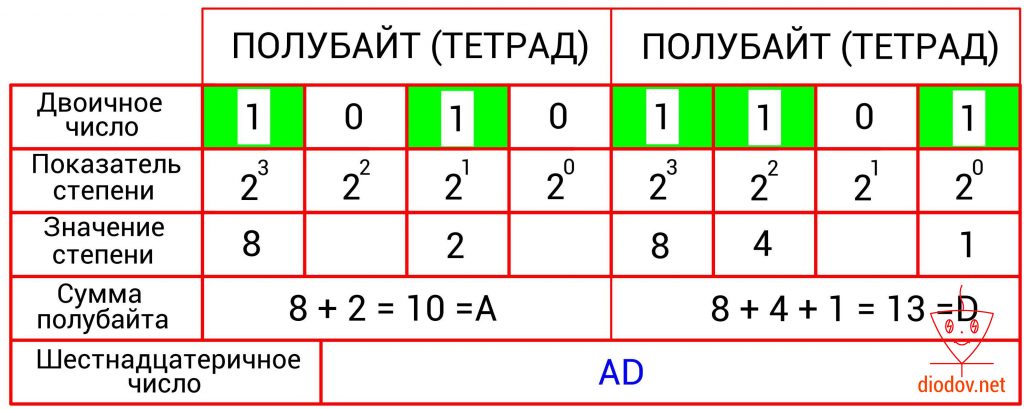
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.

Другие системы счисления

В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.

Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.

Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.

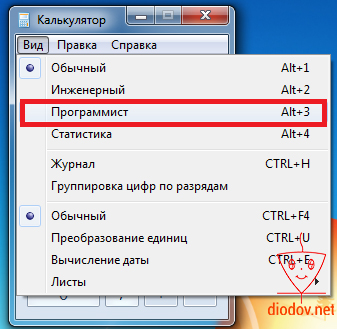
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.

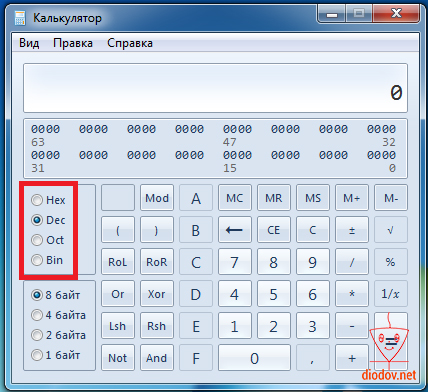
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.

В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)

Источник