Что такое волновой процесс
Лекция 6. Физика волн. Волновые процессы
Кинематика и динамика волновых процессов. Плоская стационарная и синусоидальная волна. Интерференция и дифракция волн. Бегущие и стоячие волны. Фазовая скорость, длина волны, волновое число, волновой вектор. Упругие волны в газах, жидкостях и твердых телах. Энергетические характеристики упругих волн. Вектор Умова.
6.1. Кинематика и динамика волновых процессов.
Плоская стационарная и синусоидальная волна
Волны – изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Процесс распространения колебаний в пространстве.
Распространение колебаний в пространстве происходит благодаря взаимодействию между частицами упругой среды. Волна в отличие от колебаний характеризуется не только периодичностью во времени, но и периодичностью в пространстве. Частицы среды при этом не переносятся волной, они лишь совершают колебания около своих положений равновесия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества в пространстве. Среди разнообразия волн, встречающихся в природе и технике, выделяют упругие, на поверхности жидкости и электромагнитные.
Упругими (или механическими) волнами называются механические возмущения, возникающие и распространяющиеся в упругой среде. К упругим волнам относятся звуковые и сейсмические волны; к электромагнитным – радиоволны, свет и рентгеновские лучи.
В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные и поперечные волны.
Продольные – это волны, направление распространения которых совпадает с направлением смещения (колебания) частиц среды.
Поперечные – это волны, направление распространения которых и направление смещения (колебания) частиц среды взаимно перпендикулярны.
В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому упругие деформации в них могут распространяться только в виде продольных волн (“волны сжатия”).
В твердых телах, в которых упругие силы возникают при сдвиге, упругие деформации могут распространяться не только в виде продольных, но и в виде поперечных волн (“волны сдвига”). В твердых телах ограниченного размера (например, в стержнях и пластинах) картина распространения волны более сложна: здесь возникают еще и другие типы волн, являющиеся комбинацией первых двух основных типов.
В электромагнитных волнах направления электрического и магнитного полей почти всегда перпендикулярны направлению распространения волны, (за исключением случаев анизотропных сред и распространения в несвободном пространстве) поэтому электромагнитные волны в свободном пространстве поперечны.
Волны могут иметь различную форму. Одиночной волной, или импульсом, называется сравнительно короткое возмущение, не имеющее регулярного характера. Ограниченный ряд повторяющихся возмущений называется цугом волн.
Гармоническая волна – бесконечная синусоидальная волна, в которой все изменения среды происходят по закону синуса или косинуса. Такие возмущения могут распространяться в однородной среде (если их амплитуда невелика) без искажения формы.
Геометрическое место точек, до которых доходят волны за некоторый промежуток времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченного в волновой процесс, от области, в которой колебания еще не возникли.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l. Длина волны равна расстоянию, на которое распространяется волна за один период:


T – период волны, т.е. время, за которое совершается один полный цикл колебания;
Направление волны определяется с помощью волнового вектора k. Направление волнового вектора совпадает с направлением вектора скорости:

В акустике и оптике численное значение волнового вектора представляют в виде волнового числа:

6.2. Уравнение плоской волны
 |
Эта функция должна быть периодической как относительно t, так и относительно x, у, z. Найдем вид функции 
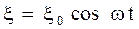
В точке пространства, расположенной на расстоянии x от места возникновения волны, частицы будут совершать те же колебания, что и в точке возникновения волны. Волновые поверхности в этом случае будут перпендикулярны к оси X. Поскольку все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от x и t x = x(x, t).
Для прохождения расстояния от места возникновения до рассматриваемой точки волне требуется время. Фронт волны придет в рассматриваемую точку пространства спустя время 
Уравнение колебаний в рассматриваемой точке будет иметь вид

Формула (6.6) представляет собой уравнение прямой бегущей волны, т.е. распространяющейся в направлении положительной полуоси X.
Бегущими волнами называются волны, которые переносят в пространстве энергию. Количественно перенос энергии волнами характеризуется вектором плотности потока энергии

Вектор плотности потока энергии – физическая величина, модуль которой равен энергии DE, переносимой волной за единицу времени (Dt=1) через единичную площадку, расположенную перпендикулярно направлению распространения волны (DS^). Направление вектора потока плотности энергии (вектора Умова) совпадает с направлением переноса энергии. Можно показать, что численное значение вектора потока плотности энергии определяется соотношением
где u – плотность энергии в каждой точке среды, среднее значение которой равно:

ρ – плотность среды;
v – фазовая скорость (скорость перемещения фазы волны).
j = u×v. (6.9)
Фазовая скорость упругих волн:
а) продольных 
б) поперечных 
где E – модуль Юнга (характеристика упругих свойств среды, обратная коэффициенту упругости);
Понятие фазовой скорости справедливо для монохроматических волн.
Так как распространяющиеся в пространстве волны представляют собой волновой пакет (в силу принципа суперпозиции), то кроме фазовой скорости, для волнового пакета вводят в рассмотрение понятие групповой скорости. Волновой пакет – совокупность волн, частоты которых мало отличаются друг от друга.
Групповой скоростью называют скорость перемещения в пространстве амплитуды волны. С ней происходит перенос энергии волны. Групповая скорость определяется следующим соотношением:

Уравнение обратной волны можно получить путем замены в (6.6) х на (-х):

Оказывается, что уравнение любой волны является решением некоторого дифференциального уравнения второго порядка, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от уравнения волны: 




Разделим обе части уравнения (6.15) на v 2 :
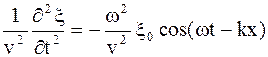

Сравнивая выражения (6.14) и (6.16), убеждаемся в равенстве их правых частей, поэтому можем приравнять левые части этих уравнений:

Соотношение (6.17) является волновым уравнением плоской волны, распространяющейся вдоль оси X.
Волновое уравнение плоской волны, распространяющейся в трехмерном пространстве, имеет вид


В математике вводят специальный оператор, называемый оператором Лапласа:


С применением оператора Лапласа /лапласиана/ волновое уравнение (6.17) принимает вид


6.4. Интерференция волн. Стоячие волны
При одновременном распространении в среде нескольких волн частицы среды совершают колебание, являющееся результатом геометрического сложения колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны накладываются одна на другую, не изменяя друг друга. Это явление называют принципом суперпозиции волн.
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают разностью фаз и имеют одинаковую частоту, волны называются когерентными. Когерентные волны излучаются когерентными источниками. Когерентными источниками называют точечные источники, размерами которых можно пренебречь, излучающие в пространство волны с постоянной разностью фаз. При сложении когерентных волн возникает явление интерференции.
Пусть вдоль оси X распространяются прямая и обратная плоские волны, уравнения которых имеют вид


В данном случае результирующее колебание получается путем алгебраического сложения:

Воспользовавшись тригонометрическим тождеством

перепишем (6.22) в виде

Амплитуда стоячей волны

Из (6.24) видно, что амплитуда, зависящая от x, может достигать максимального и минимального значений.
1) при kx = ± np (n = 0, 1, 2, ¼) амплитуда максимальна: A = 2x0. Точки, в которых амплитуда смещения удваивается, называются пучностями стоячей волны;
2) при kx = ± (2n + 1)p амплитуда обращается в нуль. Эти точки называются узлами стоячей волны.
Расстояние между соседними (узлам) – длина стоячей волны l0. Длина стоячей волны

 Рис.6.2 Рис.6.2 |
Таким образом, длина стоячей волны равна половине длины бегущей волны.
Графически стоячая волна выглядит так, как показано на рис.6.2.
В соседних полуволнах колебания частиц имеют противоположную фазу, или, как говорят, сдвиг по фазе составляет p. В отличие от бегущей волны в пределах одной полуволны колебания всех точек происходят в одной и той же фазе, но с различной амплитудой.
Очень часто стоячие волны используют для определения скорости распространения волн. Это достигается с помощью так называемого интерферометра.
 Рис.6.3 Рис.6.3 |

То есть для определения скорости распространения волны (звуковой волны) необходимо измерить длину стоячей волны l0 и частоту звуковых колебаний.
Лекция 7. Энергия, работа, мощность
Работа силы и её выражение через криволинейный интеграл. Мощность. Энергия как универсальная мера различных форм движений и взаимодействий. Кинетическая энергия системы и её связь с работой внешних и внутренних сил, приложенных к системе. Энергия системы, совершающей вращательное движение. Энергия системы, совершающей колебательное движение. Потенциальная энергия и энергия взаимодействия. Потенциальная энергия тела, находящегося в поле тяготения другого тела. Потенциальная энергия и устойчивость системы. Внутренняя энергия. Энергия упругой деформации.
7.1. Работа силы и её выражение через криволинейный интеграл
При совершении работы всегда имеются сила, действующая на материальную точку (систему, тело), и вызванное данной силой перемещение. При отсутствии хотя бы одного из этих факторов работа не совершается.
Элементарная работа некоторой силы F, действующей на материальную точку (тело, систему), вызывающей элементарное перемещение dr, равна произведению силы на перемещение:
dA = F×dr = F×dr×cosa = Fr×dr, (7.1)
Волновые процессы. Продольные и поперечные волны



Глава 19. Упругие волны
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т. е. фактически только в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением 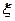
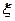
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны 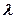
или, учитывая, что Т = 1/ 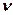
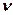
Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени — один. Волновой фронт также является волновой поверхностью. В принципе волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоскoй или сферической.
Общие сведения о волновых процессах
Все что происходит во вселенной можно описать как колебательный процесс, начиная с уровня микромира, макромира и заканчивая необозримым мегамиром. Вращение электронов по орбитам вокруг ядра атома, вращение Луны вокруг Земли, вращение Земли и планет вокруг Солнца. Эти вращательные движения по сути есть колебательные процессы, которые в свою очередь порождают различные волны. Мы их не слышим потому, что ухо человеческое настроено лишь на небольшой диапазон звуковых волн. Нас всюду окружают колебательные процессы.
Первые сейсмологические наблюдения восходят к глубокой древности. С 19 в. начал играть все большую роль в изучении глубоких недр Земли сейсмический метод. Сейсмические явления изучались геологами с самого начала как проявление мгновенных подвижек земной коры, причем высказывались различные предположения об их причинах, изучались последствия. Физики конструировали приборы для регистрации этих подземных толчков.
Теория волновых процессов – область науки, исследующая волновые явления различной природы. С колебаниями и волнами человек встречается постоянно. Существует большое многообразие волновых процессов: волны, порождаемые землетрясениями, звуковые волны, распространяющиеся в воздухе, волны механических колебаний в натянутых струнах музыкальных инструментов или в кристаллах кварца, используемые для стабилизации частоты радиопередатчика, электромагнитные волны, излучаемые антенной, и многие-многие другие. Несмотря на большое разнообразие, в колебательных процессах наблюдаются одни и те же закономерности, которые описываются одинаковыми математическими и физическими моделями и исследуются общими методами. Поэтому можно сформулировать общее определение, справедливое для любых видов волн.
Волной называется любое изменение (возмущение) состояния среды, распространяющееся с конечной скоростью и несущее энергию. Все волны можно разделить на два типа: упругие (механические) и электромагнитные.
Механической волнойназывают механические возмущения, распространяющиеся в пространстве и несущие энергию. Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости. Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.
Рассмотрим виды механических волн по отношению смещения к направлению волны. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.1) или по струне.
Рис. 2.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту
Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. 2.2) или звуковые волны в газе являются примерами таких волн.
Рис. 2.2. Распространение продольного волнового импульса по упругому стержню
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по всему объему. Так, например, любой малый элемент твердого тела обладает массой и упругостью. В простейшей одномерной модели твердое тело можно представить как совокупность шариков и пружинок (рис. 2.3).
Рис. 2.3. Простейшая одномерная модель твердого тела
В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки – жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле. В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Поперечная волна. Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия. При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна (рис. 2.4).
Рис. 2.4. Продольная и поперечная волна
В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.
Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Смещение y(x,t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:



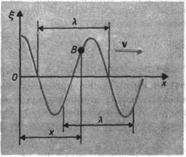
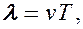
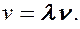





 – так называемое волновое число, ω = 2πf– круговая частота.
– так называемое волновое число, ω = 2πf– круговая частота.

 является пространственным аналогом круговой частоты
является пространственным аналогом круговой частоты 










 электромагнитной теории света Джеймса Максвелла. Герц доказал существование электромагнитных волн. Он подробно исследовал отражение, интерференцию, дифракцию и поляризацию электромагнитных волн, доказал, что скорость их распространения совпадает со скоростью распространения света, и что свет представляет собой не что иное, как разновидность электромагнитных волн.
электромагнитной теории света Джеймса Максвелла. Герц доказал существование электромагнитных волн. Он подробно исследовал отражение, интерференцию, дифракцию и поляризацию электромагнитных волн, доказал, что скорость их распространения совпадает со скоростью распространения света, и что свет представляет собой не что иное, как разновидность электромагнитных волн.