Что такое внутренняя точка в геометрии
Внутренняя точка
Вну́тренняя то́чка мно́жества в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью.
Содержание
Определение
Замечания
Частные случаи
См. также
Полезное
Смотреть что такое «Внутренняя точка» в других словарях:
ВНУТРЕННЯЯ ТОЧКА — множества в топологическом пространстве точка, входящая в данное множество вместе с нек рым открытым множеством, ее содержащим. Если х В. т. множества А, то Аназ. окрестностью точки x В широком Смысле. С. М. Сирота … Математическая энциклопедия
Внутренняя точка множества — в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью. Содержание 1 Определение 2 Замечания 3 Частные сл … Википедия
Внутренняя империя — INLAND EMPIRE Жанр драма … Википедия
Внутренняя форма слова — «ВНУТРЕННЯЯ ФОРМА СЛОВА» название книги Г Г. Шпета «Внутренняя форма слова: Этюды и вариации на темы Гумбольдта» (М., 1927); и одновременно центральное понятие, используемое им для обозначения существенно смысловых связей и отношений.… … Энциклопедия эпистемологии и философии науки
ВНУТРЕННЯЯ СЕКРЕЦИЯ — ВНУТРЕННЯЯ СЕКРЕЦИЯ, обозначение выделения изнутри клетки наружу от нее, не через выводной проток, определенных веществ, к рые или здесь же или (что более обычно) вдялч от места выделения действуют регулирующим образом на те или иные функции… … Большая медицинская энциклопедия
Внутренняя метрика — Внутренняя метрика тип метрик такой, что для любой пары точек есть точка, находящаяся почти на полпути между ними. Содержание 1 Определение 2 Связанные определения 3 … Википедия
Внутренняя группа — Подвздошно поясничная мышца (m. iliopsoas) (рис. 90, 109, 129, 130) сгибает бедро в тазобедренном суставе, вращая его кнаружи. При фиксированном положении бедра сгибает поясничный отдел и таз, наклоняя туловище вперед. Мышца образуется в… … Атлас анатомии человека
Точка (тактический ракетный комплекс) — У этого термина существуют и другие значения, см. Точка. Точка индекс ГРАУ 9K79 обозначение НАТО SS 21 Scarab A, по договору РСМД ОТР 21 … Википедия
Внутренняя точка множества
Связанные понятия
Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Метри́ческим простра́нством называется непустое множество, в котором между любой парой элементов, обладающих определенными свойствами, определено расстояние, называемое ме́трикой.
В математике монодро́ми́ей называется явление, состоящее в преобразовании некоторого объекта при обнесении его вдоль нетривиального замкнутого пути.
Если дано топологическое пространство и группа действий на нём, образы отдельной точки под действием группы действий образуют орбиты действий. Фундаментальная область — это подмножество пространства, которое содержит в точности по одной точке из каждой орбиты. Она даёт геометрическую реализацию абстрактного множества представителей орбит.
Отношение инцидентности — это бинарное отношение между двумя различными типами объектов. Это включает понятия, которые можно выразить такими фразами как «точка лежит на прямой» или «прямая принадлежит плоскости». Наиболее существенное отношение инцидентности — между точкой P и прямой l, которое записывается как P I l. Если P I l, пара (P, l) называется флагом. В разговорном языке существует много выражений, описывающих отношение инцидентности (например, прямая проходит через точку, точка лежит на.
Выпуклые метрические пространства интуитивно определяются как метрические пространства с таким свойством, что любой «отрезок», который соединяет две точки этого пространства, содержит другие точки, кроме своих концов.
Как и для криволинейных интегралов, существуют два рода поверхностных интегралов.
В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.
ВНУТРЕННЯЯ ТОЧКА
Смотреть что такое «ВНУТРЕННЯЯ ТОЧКА» в других словарях:
Внутренняя точка — множества в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью. Содержание 1 Определение 2 Замечания 3 Частные случаи 4 … Википедия
Внутренняя точка множества — в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью. Содержание 1 Определение 2 Замечания 3 Частные сл … Википедия
Внутренняя империя — INLAND EMPIRE Жанр драма … Википедия
Внутренняя форма слова — «ВНУТРЕННЯЯ ФОРМА СЛОВА» название книги Г Г. Шпета «Внутренняя форма слова: Этюды и вариации на темы Гумбольдта» (М., 1927); и одновременно центральное понятие, используемое им для обозначения существенно смысловых связей и отношений.… … Энциклопедия эпистемологии и философии науки
ВНУТРЕННЯЯ СЕКРЕЦИЯ — ВНУТРЕННЯЯ СЕКРЕЦИЯ, обозначение выделения изнутри клетки наружу от нее, не через выводной проток, определенных веществ, к рые или здесь же или (что более обычно) вдялч от места выделения действуют регулирующим образом на те или иные функции… … Большая медицинская энциклопедия
Внутренняя метрика — Внутренняя метрика тип метрик такой, что для любой пары точек есть точка, находящаяся почти на полпути между ними. Содержание 1 Определение 2 Связанные определения 3 … Википедия
Внутренняя группа — Подвздошно поясничная мышца (m. iliopsoas) (рис. 90, 109, 129, 130) сгибает бедро в тазобедренном суставе, вращая его кнаружи. При фиксированном положении бедра сгибает поясничный отдел и таз, наклоняя туловище вперед. Мышца образуется в… … Атлас анатомии человека
Точка (тактический ракетный комплекс) — У этого термина существуют и другие значения, см. Точка. Точка индекс ГРАУ 9K79 обозначение НАТО SS 21 Scarab A, по договору РСМД ОТР 21 … Википедия
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
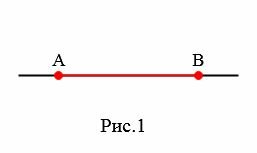 |
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
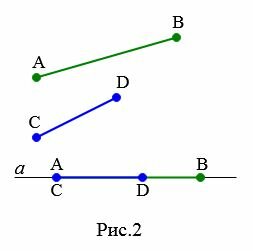 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
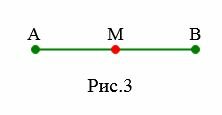 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
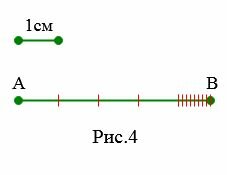 |
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
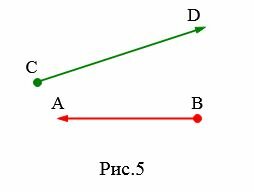 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Точки, Прямые и Отрезки — Определения и Свойства
Вспомним определения точки и прямой:
Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.
Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.
Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.
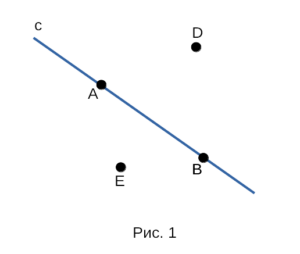
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.
Через любые две точки можно провести прямую,
и притом только одну.
Если две прямые имеют общую точку, то можно сказать,
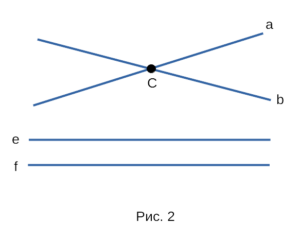
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.
Две прямые имеют только одну общую точку,
либо не имеют общих точек.
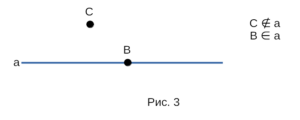
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.
Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.