Что такое внешняя и внутренняя область угла
Что такое внешняя и внутренняя область угла
Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.
Обозначение углов
Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.
Внутренняя и внешняя область
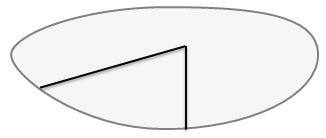
Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:
Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.
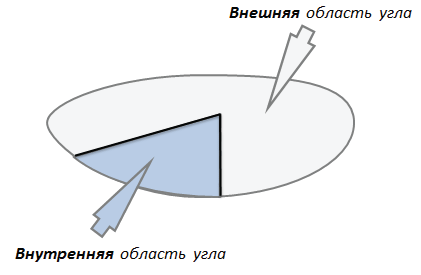
Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:
Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.
Что такое внешняя и внутренняя область угла
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
 |
Обозначение угла
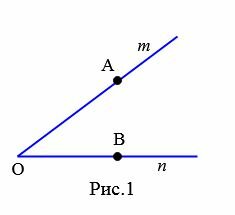
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
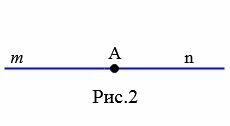
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
 |
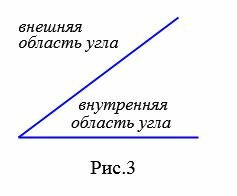
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
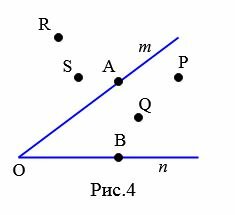
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
 |
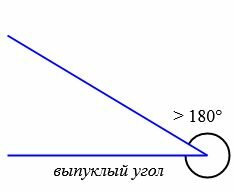
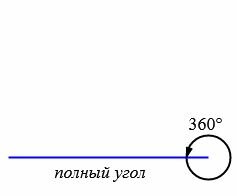
Типы углов
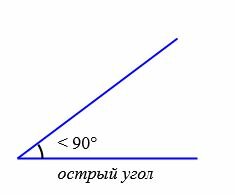
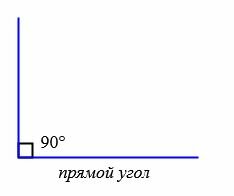
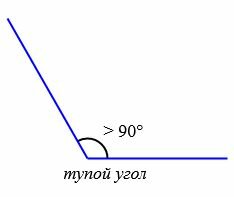
В зависимости от величин, углы бывают следующих типов (Рис.5):
  |
  |
  |
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
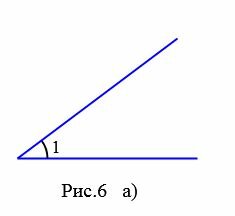 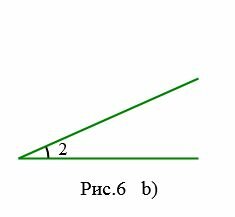 |
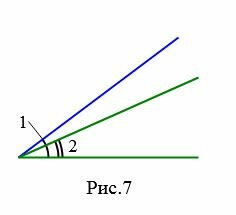
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
 |
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Что такое внешняя и внутренняя область угла
Угол – геометрическая фигура, образованная двумя лучами, исходящими из одной точки.
Точка, из которой исходят лучи, образующие угол, называется вершиной угла. Лучи, образовавшие угол – его сторонами.
Угол может быть назван по имени его вершины или по имени лучей, которые его образовали. Но лучше всего назвать угол, как и луч, по имени отрезков лучей, образующих его, при том, что вершина угла является начальной точкой обоих этих отрезков.

Градусная мера угла
Угол обладает градусной мерой. Представьте себе, что изначально оба луча, образующие угол, совпадали. Можете вспомнить циферблат часов в полдень, когда минутная и часовая стрелка перекрывают друг друга. Со временем минутная стрелка будет все дальше отходить от часовой, но при этом они все равно будут иметь общую точку – ось, на которую они надеты.
Независимо от величины часов, длины стрелок, все часы показывают одинаковое время. То есть, их стрелки со временем расходятся на один и тот же градус, хотя между их концами разное расстояние. В три часа пополудни угол между стрелками будет равен 90 градусов; в шесть вечера – 180. Градусные меры остальных углов рассчитываются, исходя из этих значений. То есть, в два часа дня угол между минутной и часовой стрелкой будет равен 60 градусов; в час дня – 30 градусов.
Угол, равный 180 градусов, называется развернутым
Внутренняя и внешняя область угла
Неразвернутый угол имеет внутреннюю и внешнюю области.
Внутренней областью угла является часть площади, ограниченная образующими его лучами, через которую проходит прямая, соединяющие две точки на этих лучах.
Если из вершины угла выходит луч, не совпадающий со сторонами угла, и проходящий по внутренней области угла, то он делит этот угол на два угла, сумма градусных мер которых равна градусной мере угла
Если луч делит угол на два равных угла, то он называется биссектрисой угла
Методы измерения углов
Градусную меру углов можно измерить различными способами. Наиболее простым является применение транспортира.
Измерение производится так:
Есть несколько единиц измерения углов – по аналогии с единицами измерения времени. 1 градус состоит из 60 минут, 1 минута – из 60 секунд.
Есть особые названия для углов, зависящие от их градусной меры:
Построение углов
В задачах бывает нужно построить угол с определенной градусной мерой. Делается это при помощи транспортира. Порядок построения такой:
Задачи
Задача 1
Короткая запись условия:
Вопрос: Проходит ли луч ОС между сторонами угла АОВ?
Решение и чертеж
Задача 2
Вопрос: докажите, что все точки лежат на одной прямой.
Короткая запись условия:
Задача 3
Вопрос: Докажите, что все четыре прямые пересекаются в одной точке.
Короткая запись условия:
Доказательство
Задача 4
Короткая запись условия:
Доказательство и чертёж
Как производится измерение транспортиром
Транспортир накладывается на угол
Центральная точка транспортира совмещается с вершиной угла
Прямая сторона выреза инструмента совмещается с одной из сторон угла
Число, на которое укажет вторая сторона угла, и есть градусная мера этого угла
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Стороны угла – лучи, из которых состоит угол.
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Теоретический материал для самостоятельного изучения.
Мы уже познакомились с некоторыми геометрическими понятиями: прямая, точка, отрезок. Сегодня мы рассмотрим ещё два понятия, часто встречающиеся в геометрии – это луч и угол.
Для начала, вспомним, как строятся и обозначаются лучи и углы.
Для этого проведём прямую а, отметим на ней точкуО, которая разделит прямую на две части. Эти части прямой называются лучами, исходящими из точки О. А сама точка О, называется началом каждого из лучей.
Луч принято обозначать как одной малой латинской буквой, например, а.
Или двумя большими латинскими буквами, например, ОА.
При этом стоит помнить, что первая буква всегда обозначает начало луча, а вторая– это любая точка на луче.
Теперь рассмотрим понятие угол.
Начнём с определения.
Угол – это часть плоскости, ограниченная двумя лучами с общим началом.
Лучи – это стороны угла.
В данном случае, это стороны ОА и ОВ.
Общее начало сторон, в данном случае О – это вершина угла.
Углы принято обозначать как двумя малыми латинскими буквами, по названию сторон угла, например, ∠hk,
так и тремя большими латинскими буквами, например, тот же угол можно обозначить ∠АОВ, где вершина угла будет стоять в середине обозначения угла.
Или одной большой латинской буквой, обозначающей вершину угла. Например, тот же угол можно обозначить буквой∠О, по вершине угла.
Далее введём понятия, связанные с углами.
Во-первых, рассмотрим угол, который называют развёрнутым, его обе стороны лежат на одной прямой. Например, ∠С– развёрнутый.
В дальнейшем будем рассматривать углы меньше развёрнутого.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Во-вторых, плоскость, на которой изображён любой угол, кроме развёрнутого, делится на две области: внутреннюю и внешнюю.
В развёрнутом углу, любая часть считается внутренней.
На рисунке изображён угол. Какие из точек лежат внутри угла и вне его?
Внутри угла лежат точки: М, Е, К.
Вне угла лежат точки: Р, D, N.
Отметим, что точкиВ и С лежат на сторонах углаО.
Продолжая изучать углы, отметим, что если внутри угла из его вершины провести луч, то он разделит угол на два угла.
Например, луч ОС делит ∠АОВ на два угла – ∠ВОС и ∠АОС.
Итак, сегодня мы повторили некоторые сведения о луче и углах; сформировали представления о внутренней и внешней областях угла, меньше развернутого, познакомились с различными обозначениями луча и угла.
Материал для углубленного изучения
Мы разобрали понятие угол, связанное с планиметрией. Но как отмечалось ранее, у геометрии есть ещё один раздел – стереометрия, который изучается в старших классах. Этот раздел изучает пространственные фигуры, одна из таких фигур–двугранный угол. Дадим ему определение: двугранный угол – пространственнаягеометрическая фигура, образованная двумяполуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Двугранный угол имеет стороны (иначе их называют грани), это полуплоскости α и β, и ребро, в данном случае это прямая АВ. Как измерить такие углы и их разновидности, вы узнаете в курсе геометрии 10 класса.
№ 1. Какие из точек лежат на стороне угла?
Посмотрите на рисунок. На нём изображён угол ВОС, соответственно точки B и C лежат на сторонах угла, других точек нет.
№ 2. Сколько углов изображено на рисунке?
Решение. Перечислим все углы, изображённые на рисунке.
СОВ, ВОА, АОD, DОС и развёрнутые углы СОА и DОВ. Получается 8 углов.
Что такое внешняя и внутренняя область угла
Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)
Обозначения угла
На сторонах угла не отмечены точки (только обозначены большими латинскими буквами А и В)
Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)
Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)
Читаем: угол АОВ
Пишем: 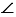
На сторонах угла отмечены и обозначены произвольные точки А и В
Читаем: угол АОВ
Пишем: 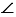
Стороны угла (лучи) обозначены малыми латинскими буквами k и m
Читаем: угол km
Пишем: 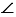
Обозначена только вершина угла
Читаем: угол О
Пишем: 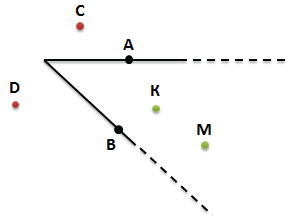
Развернутый угол
Построим прямую АВ и отметим на этой прямой точку О
Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)
Угол АОВ называется развернутым
Угол на плоскости
Изобразим часть плоскости
(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)
Построим на этой плоскости неразвернутый угол
Замечание
Любой угол разделяет плоскость на две части. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.
Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла.
Расположение точек относительно угла
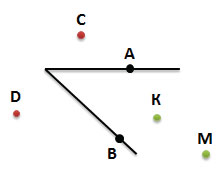
По рисунку определим положение отмеченных точек A, B, C, D, K, M
Точки А и В лежат на сторонах угла
Точки D и C лежат вне угла (во внешней области угла)
Точки К и М, лежат внутри угла (во внутренней области угла)
При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М
Поделись с друзьями в социальных сетях: