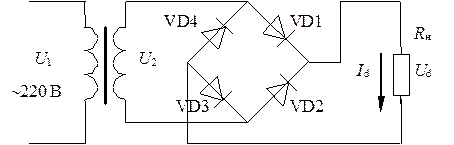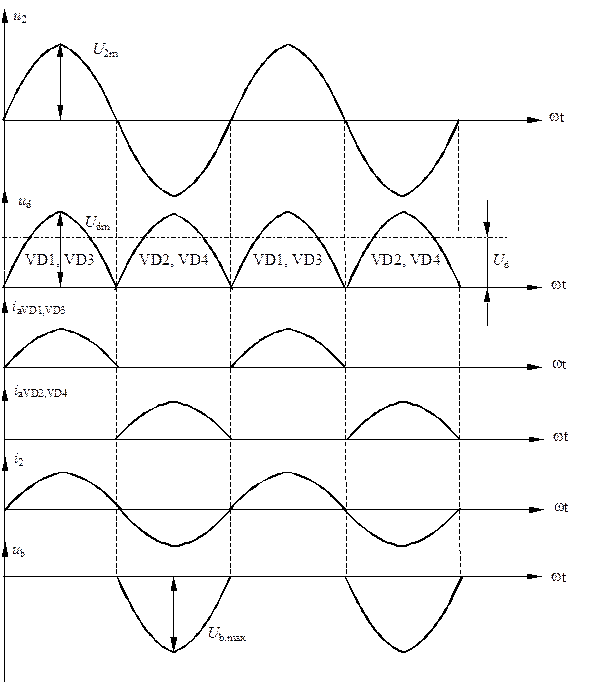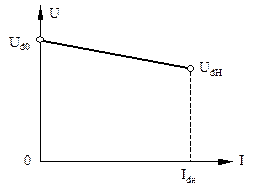Что такое внешняя характеристика выпрямителя и что она характеризует
Внешние характеристики выпрямителей
Внешней характеристикой выпрямителя называется зависимость среднего значения напряжения, подводимого к нагрузке, от среднего значения тока нагрузки. В выпрямителе без фильтра эта характеристика близка к линейной зависимости, для которой справедливо уравнение
где 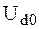
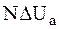
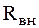
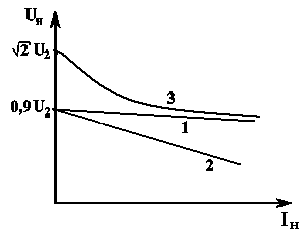
Рисунок 6.11. Внешние характеристики выпрямителей
При рассмотрении принципа работы выпрямителей пренебрегалось падением напряжения в обмотках трансформатора и диодах, что справедливо в отсутствии тока в цепи нагрузки. Таким образом, соотношение (6.2) определяет напряжение на выходе выпрямителя в режиме холостого хода, что отражено обозначением первого слагаемого правой части соотношения (6.10). На рис. 6.11 прямой «1» представлена внешняя характеристика выпрямителя без фильтра, построенная с учетом того, что 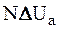
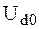
Прямая «2» на рис. 6.11 соответствует внешней характеристике выпрямителя, работающего с индуктивным фильтром. Кроме индуктивного, реальный фильтр имеет и активное сопротивление. Поскольку индуктивный фильтр с нагрузкой включен последовательно, наличие этой компоненты сопротивления фильтра эквивалентно увеличению значения внутреннего сопротивления выпрямителя, то есть сомножителя в третьем слагаемом правой части соотношения (6.10). Поэтому внешняя характеристика выпрямителя с индуктивным фильтром представляется прямой линией, но имеющей больший наклон, чем характеристика без фильтра.
Как отмечалось в предыдущем разделе, в режиме холостого хода напряжение на выходе выпрямителя с емкостным фильтром равно амплитуде переменного напряжения, снимаемого со вторичной обмотки трансформатора при мостовой схеме или с одной из ее половин при схеме с нулевым отводом, т.е. при нулевом токе нагрузки напряжение 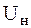
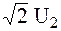
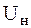
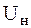
Дата добавления: 2016-01-20 ; просмотров: 5983 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Внешние характеристики выпрямителя
Внешней или нагрузочной характеристикой выпрямителя называют зависимость напряжения на нагрузке UH от тока нагрузки Iн
Характер этой зависимости можно уяснить из рис. 99.
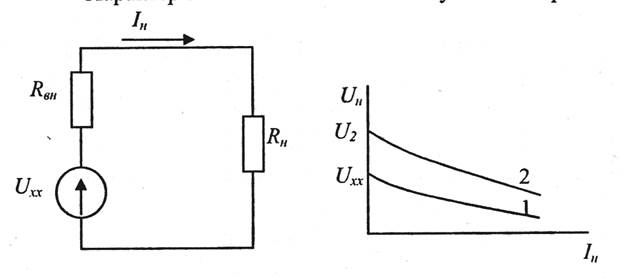
Рис. 99. Эквивалентная схема выпрямителя и его внешние характеристики
Выпрямитель можно рассматривать как источник напряжения постоянного тока с некоторой эквивалентной ЭДС, равной напряжению холостого хода Uxx, (напряжению на выходе выпрямителя при токе нагрузки Iн = 0) и внутренним сопротивлением Rвн,
Из эквивалентной схемы следует, что
Выражение показывает, что с ростом выпрямленного тока Iн падение напряжения на Rвн увеличивается и напряжение Uн, на нагрузке уменьшается. Сопротивление диодов в прямом направлении зависит от тока, поэтому внешняя характеристика Iн = f(Uн) является нелинейной. Однако при малом сопротивлении цепи выпрямителя эта нелинейность может быть слабо выражена.
На внешних характеристиках выпрямителя кривая 1 без сглаживающего фильтра и кривая 2 с емкостным фильтром. Кривая 2 расположена выше. Это объясняется тем, что при наличии емкостного фильтра в режиме холостого хода (при Iн = 0) конденсатор Сф заряжается до амплитудного значения выпрямленного напряжения UH = U2m, что по величине больше, чем среднее значение выпрямленного напряжения в отсутствие сглаживающего фильтра. Примерно такая же картина будет и при применении Г-образного или П-образного фильтров.
Дата добавления: 2015-09-11 ; просмотров: 2374 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Внешняя характеристика мостового выпрямителя
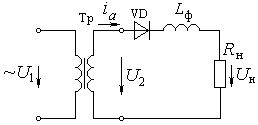
Схема однофазного мостового выпрямителя представлена на рис. 3.5. В данной схеме у трансформатора только одна вторичная обмотка, но в нагрузку поступают два полупериода напряжения вторичной обмотки трансформатора. В нечётные полупериоды ток проходит через диод VD1, нагрузку, диод VD3. В чётные – через диод VD2, нагрузку, диод VD4.
Рис. 3.5. Однофазный мостовой выпрямитель
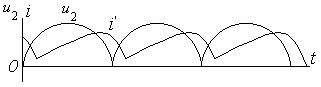
Временная диаграмма работы однофазного мостового выпрямителя представлена на рис. 3.6. Она практически не отличается от временной диаграммы двухполупериодного выпрямителя, только лишь отмечено прохождение тока через пары диодов VD1, VD3 и VD2, VD4, а также видно, что обратное напряжение на закрытом диоде Ub.max уменьшилось.
Среднее значение выпрямленного напряжения такое же, как в предыдущей схеме:

Рис. 3.6. Временная диаграмма работы однофазного мостового выпрямителя
Среднее значение тока диода 
Максимальное обратное напряжение на диоде равно амплитудному значению напряжения вторичной обмотки:

Подмагничивания сердечника трансформатора нет, что является существенным преимуществом данной схемы. Подробнее рассмотрим режим работы трансформатора.
Действующее значение тока вторичной обмотки:

Действующее значение напряжения вторичной обмотки трансформатора:

Расчетная мощность вторичной обмотки трансформатора:
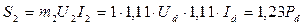
Расчетная мощность первичной обмотки:
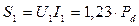
Расчетная (типовая) мощность трансформатора:
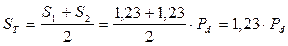
Коэффициент использования трансформатора по мощности:
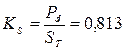
Для удобства сравнения различных схем выпрямителей составим таблицу основных электрических параметров.
Основные электрические параметры однофазных выпрямителей
| Схема выпрямителя | Трансформатор | Диоды | Нагрузка КП(1) | ||||||
| Ud/U2 | I2/Id | I1/nId | S1/Pd | S2/Pd | ST/Pd | Ub.max Ud | Ia/Id | ||
| Однофазная однополупериодная | 0,45 | 1,57 | 1,21 | 2,69 | 3,49 | 3,09 | 1,57 | 1,57 | |
| Однофазная двухполупериодная | 0,9 | 0,79 | 1,11 | 1,23 | 1,73 | 1,48 | 3,14 | 0,5 | 0,667 |
| Однофазная мостовая | 0,9 | 1,11 | 1,11 | 1,23 | 1,23 | 1,23 | 1,57 | 0,5 | 0,667 |
Проведённый анализ работы схем выпрямителей не учитывал влияние на выходное напряжение выпрямителя внутреннего сопротивления трансформатора и сопротивления диодов, а также потерь из-за прямого падения напряжения на открытых диодах.
На холостом ходу выпрямителя выходное напряжение будет меньше расчётного на величину прямого падения напряжения на открытых диодах. Для однополупериодной и двухполупериодной схемы последовательно с нагрузкой включён только один диод, а в мостовой схеме – два. Поэтому мостовая схема для малых выходных напряжений не применяется, так как падение напряжения на двух диодах существенно снижает коэффициент полезного действия схемы. Предположим, выходное напряжение выпрямителя равно 3 В. На каждом из диодов мостовой схемы прямое падение напряжения составит около 1 В, итого 2 В. То есть трансформатор должен иметь на вторичной обмотке запас по напряжению в 40% из-за потерь в диодах.
Под нагрузкой выходное напряжение выпрямителя начнёт уменьшаться из-за потерь напряжения на внутреннем сопротивлении трансформатора и диодов. Зависимость выходного напряжения выпрямителя от тока нагрузки называется внешней характеристикой.
Уравнение внешней характеристики:
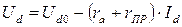
где Ud0 – напряжение холостого хода выпрямителя;
ra – активное сопротивление трансформатора;
rпр – прямое динамическое сопротивление диодов;
Как следует из выражения (3.14) внешняя характеристика выпрямителя, работающего на активную нагрузку, представляет собой прямую линию. Примерный вид внешней характеристики представлен на рис. 3.7.
Рис. 3.7. Внешняя характеристика выпрямителя с активной нагрузкой
Контрольные вопросы
1. Для чего применяются выпрямители?
2. Приведите классификацию и перечислите основные параметры выпрямителей.
3. Нарисуйте схему однополупериодного однофазного выпрямителя с активной нагрузкой и его временную диаграмму работы.
4. Нарисуйте схему двухполупериодного однофазного выпрямителя с активной нагрузкой и его временную диаграмму работы.
5. Нарисуйте схему мостового однофазного выпрямителя с активной нагрузкой и его временную диаграмму работы.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9490 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
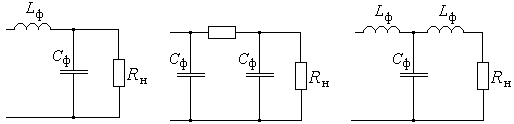
Индуктивный фильтр
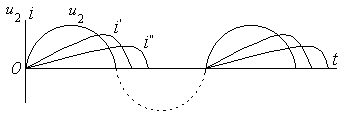
В течение положительного полупериода напряжения u2, когда ток i нарастает, индуктивная катушка Lф запасает энергию, а в отрицательный полупериод – энергия расходуется на поддержание тока.
Длительность импульсов тока iн определяется постоянной времени 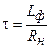
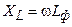
Обычно индуктивность Lф в однополупериодных схемах не применяют, а используют в двухполупериодных:
Разновидности сглаживающих фильтров:
LC— RC-фильтры; Г-, П-, Т- образные фильтры.
Сопротивление нагрузки Rн при работе изменяется, что вызывает изменение нагрузочного тока Iн.
Трансформаторы и вентили (диоды) имеют определенные величины активных сопротивлений Rтр и Rпр. На этих сопротивлениях происходит падение напряжения от тока Iн, приводящее к изменению напряжения на нагрузке Uн.
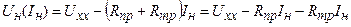
где Uхх – выпрямленное напряжение при Iн=0;
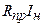
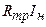
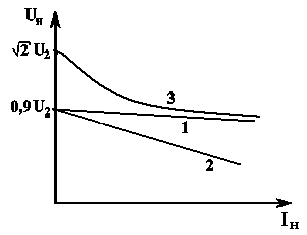
Внешняя характеристика определяет границы изменения нагрузочного тока, при котором выпрямленное напряжение не снижается ниже допустимой величины.
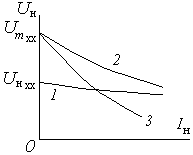 |
1 – выпрямитель без фильтра (характеристика нелинейна из-за Rпр);
2 – Выпрямитель с емкостным фильтром;
В режиме ХХ (Iн=0) выпрямленное напряжение равно амплитудному значению Umхх, а без фильтра – среднему значению.
Для однополупериодного выпрямителя 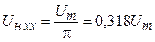
Для двухполупериодного — 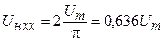
При росте тока нагрузки кривая 2 падает более резко, поскольку падение происходит также за счет более быстрого разряда конденсатора на меньшее сопротивление, что снижает напряжение на нагрузке.
3 – Выпрямитель с Г-образным RC-фильтром. Дополнительное снижение напряжения вызвано падением напряжения на последовательно включенном резисторе Rф.
Дата добавления: 2014-12-16 ; Просмотров: 4182 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Внешней характеристикой выпрямителя называется зависимость среднего значения напряжения, подводимого к нагрузке, от среднего значения тока нагрузки. В выпрямителе без фильтра эта характеристика близка к линейной зависимости, для которой справедливо уравнение
UH = Udo — 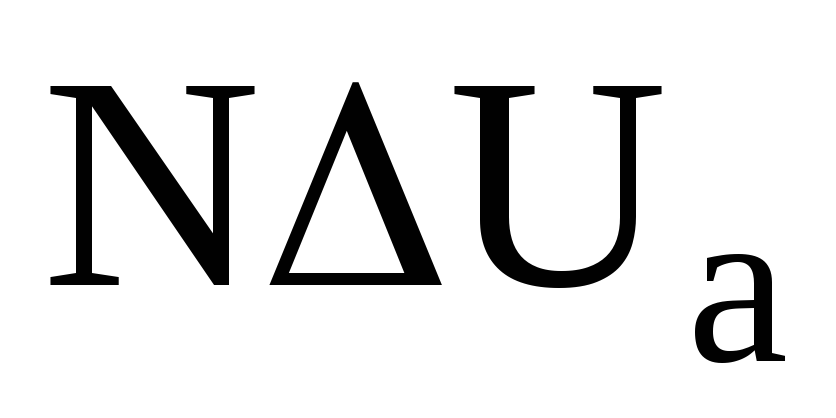

где 
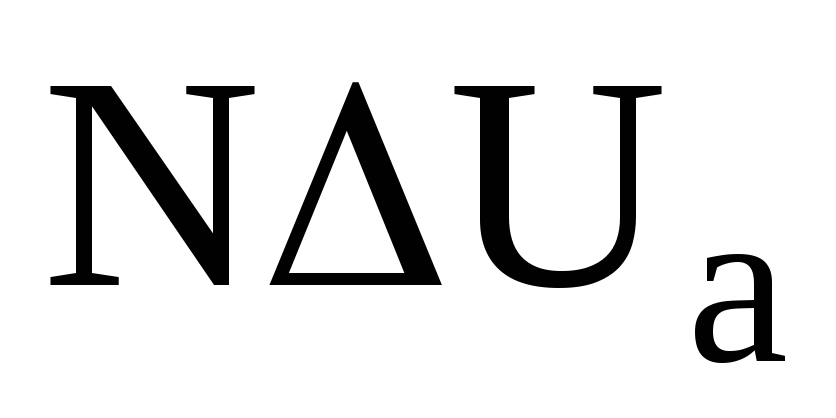

Рисунок 6.11. Внешние характеристики выпрямителей
При рассмотрении принципа работы выпрямителей пренебрегалось падением напряжения в обмотках трансформатора и диодах, что справедливо в отсутствии тока в цепи нагрузки. Таким образом, соотношение (6.2) определяет напряжение на выходе выпрямителя в режиме холостого хода, что отражено обозначением первого слагаемого правой части соотношения (6.10). На рис. 6.11 прямой «1» представлена внешняя характеристика выпрямителя без фильтра, построенная с учетом того, что 

Прямая «2» на рис. 6.11 соответствует внешней характеристике выпрямителя, работающего с индуктивным фильтром. Кроме индуктивного, реальный фильтр имеет и активное сопротивление. Поскольку индуктивный фильтр с нагрузкой включен последовательно, наличие этой компоненты сопротивления фильтра эквивалентно увеличению значения внутреннего сопротивления выпрямителя, то есть сомножителя в третьем слагаемом правой части соотношения (6.10). Поэтому внешняя характеристика выпрямителя с индуктивным фильтром представляется прямой линией, но имеющей больший наклон, чем характеристика без фильтра.
Как отмечалось в предыдущем разделе, в режиме холостого хода напряжение на выходе выпрямителя с емкостным фильтром равно амплитуде переменного напряжения, снимаемого со вторичной обмотки трансформатора при мостовой схеме или с одной из ее половин при схеме с нулевым отводом, т.е. при нулевом токе нагрузки напряжение 
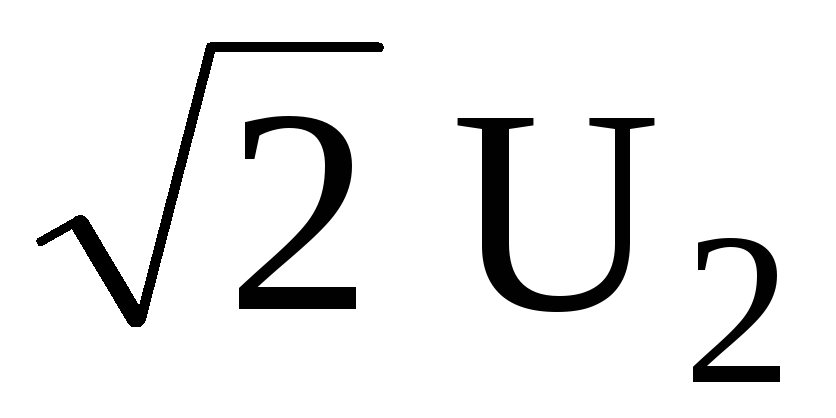


6.7. Стабилизатор напряжения
Известны два типа стабилизаторов напряжения: параметрические и компенсационные. В стабилизаторе первого типа используются свойства электронных приборов, вольт-амперная характеристика которых обеспечивает малые изменения напряжения при существенном изменении тока. К числу таких приборов относится стабилитрон. В стабилизаторах второго типа осуществляется автоматическое поддержание неизменным значения выходного напряжения. Схема параметрического стабилизатора напряжения существенно проще схемы компенсационного. Это определяет целесообразность рассмотрения принципа стабилизации выпрямленного напряжения на примере параметрического стабилизатора.
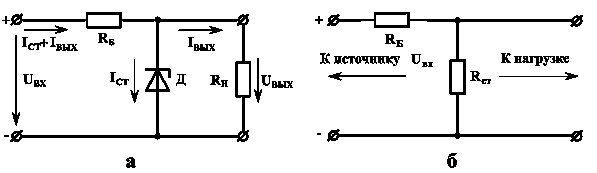
Рисунок 6.12. Параметрический стабилизатор на стабилитроне:
а – схема построения, б – эквивалентная схема
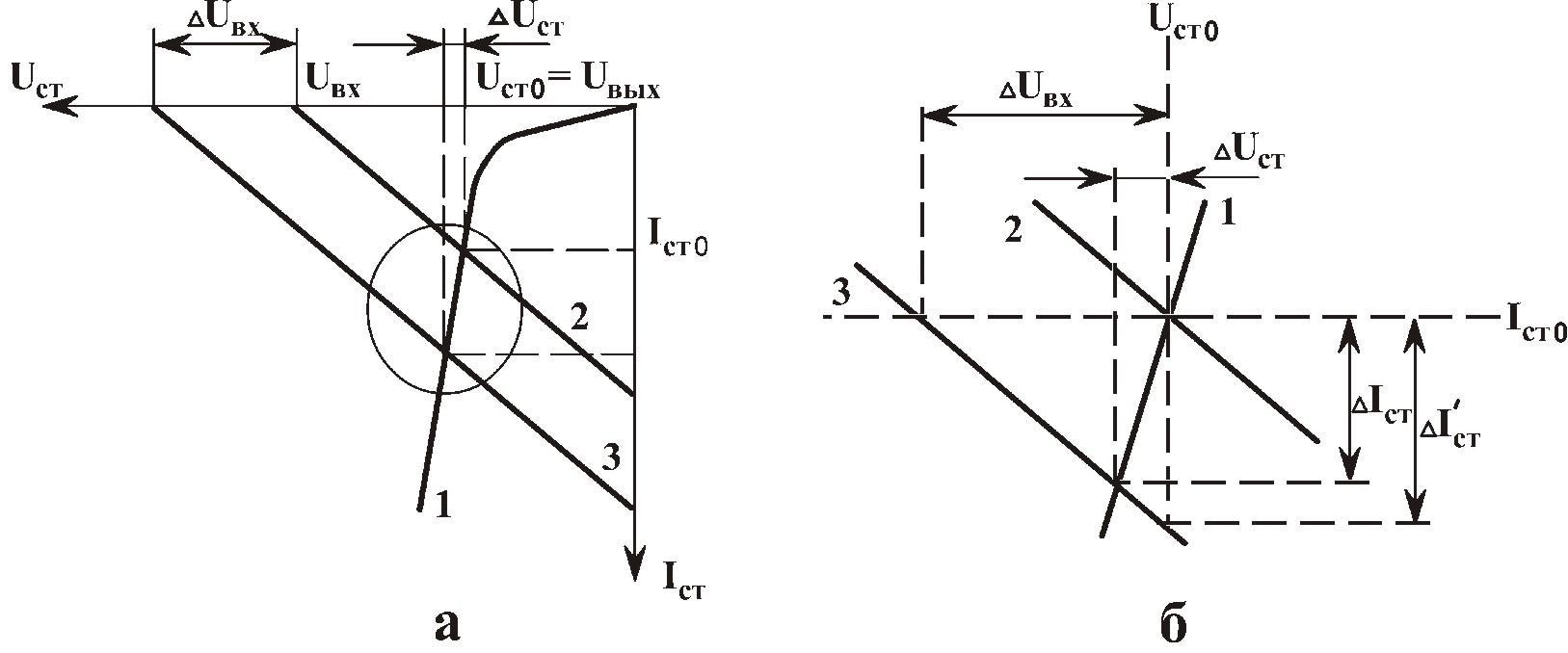
Рисунок 6.13. Построения, иллюстрирующие стабилизацию выходного
напряжения при изменении напряжения на входе
Схема параметрического стабилизатора постоянного напряжения, использующая стабилитрон, приведена на рис. 6.12,а. На рис. 6.13 представлена его вольт-амперная характеристика, которая обозначена цифрой «1». Стабилитрон подключен параллельно нагрузке, так что его напряжение определяет напряжение нагрузки. Для обеспечения стабильности выходного напряжения при изменении выходного тока необходимо, чтобы сопротивление нагрузки было существенно больше выходного сопротивления стабилизатора, последнюю величину можно определить с использованием эквивалентной схемы, приведенной на рис. 6.12,б. С учетом малой величины внутреннего сопротивления источника напряжения (то есть выходного сопротивления выпрямителя), а также малой величины статического сопротивления стабилитрона 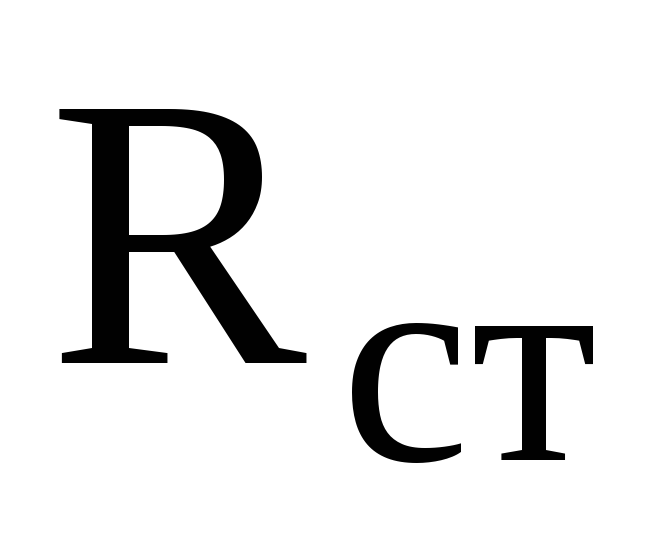
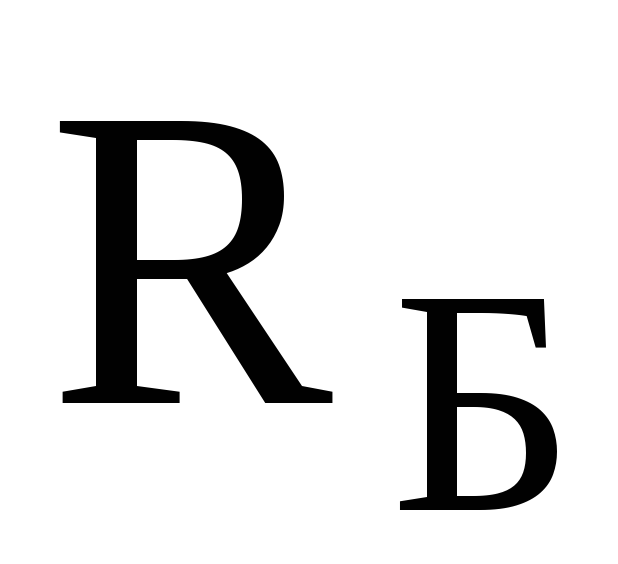
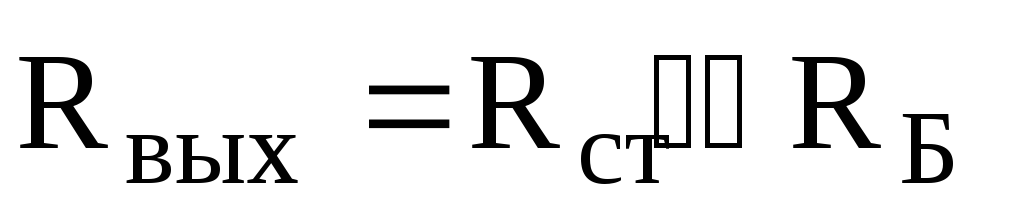
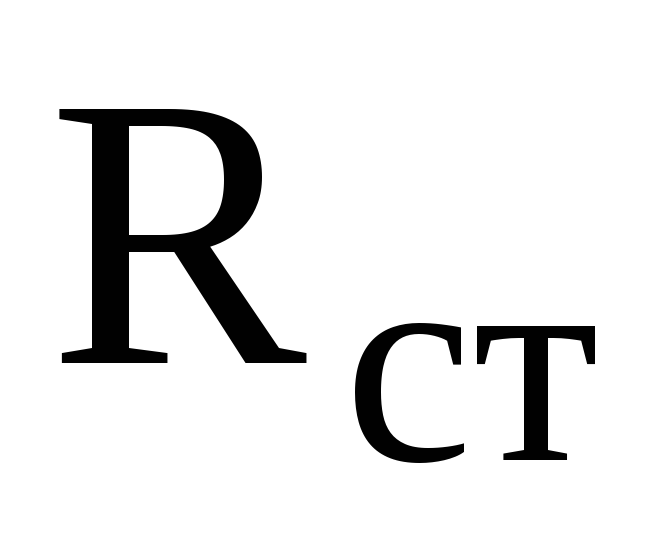
Следовательно, статическое сопротивление стабилитрона для достижения наибольшей стабилизации напряжения при изменении тока нагрузки должно быть много меньше сопротивления нагрузки.
Электрический режим стабилитрона, характеризуемый током IСТО и напряжением UСТО, находится при решении уравнения состояния, записанного по второму закону Кирхгофа для контура, включающего стабилитрон и балластное сопротивление
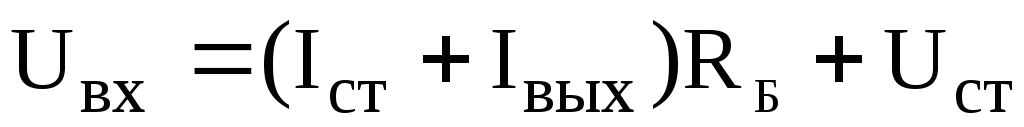
где 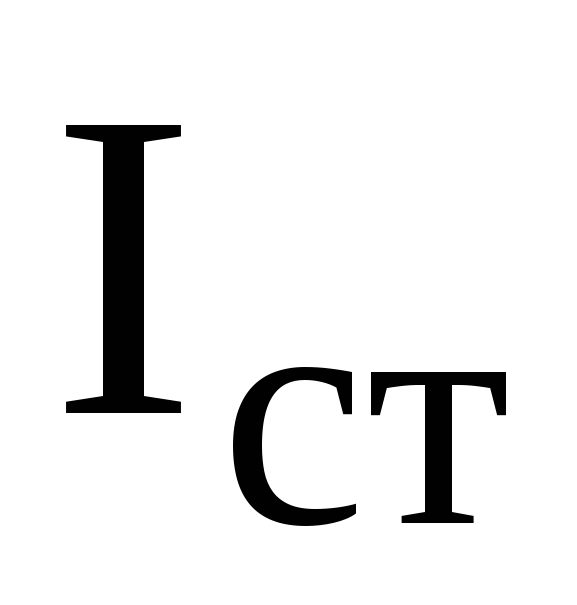

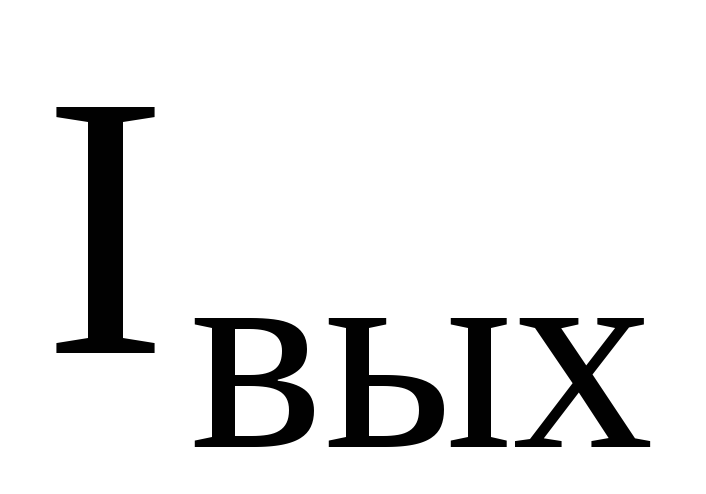
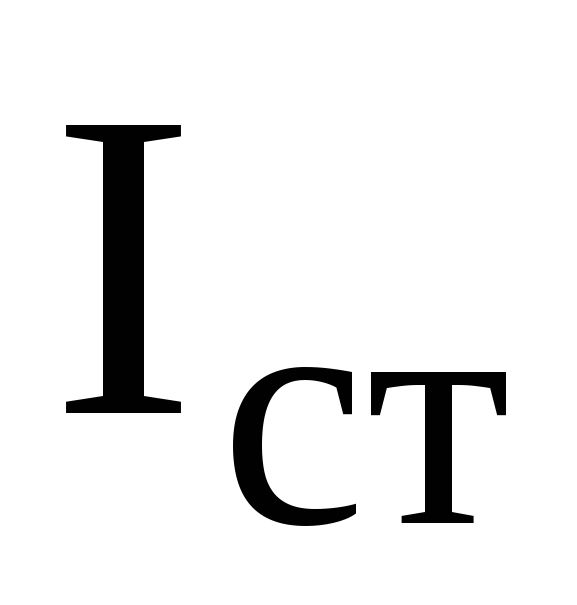
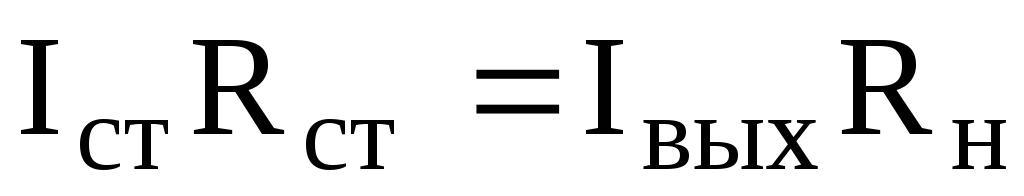
где 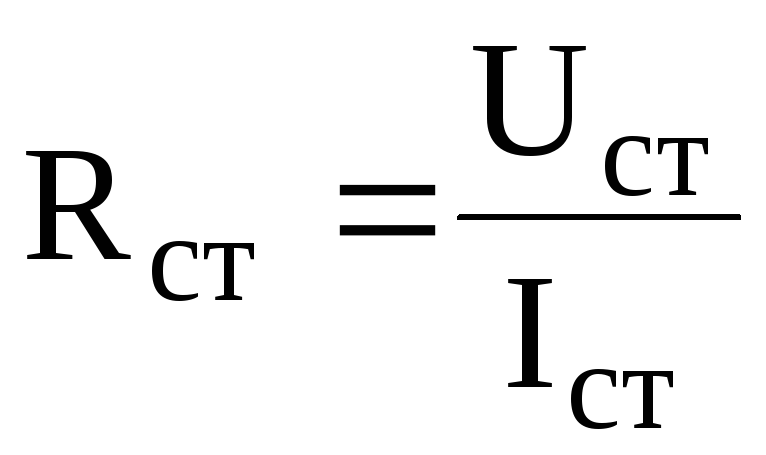
Поскольку величина статического сопротивления стабилитрона много меньше сопротивления нагрузки, уравнение (6.11) можно записать в виде:
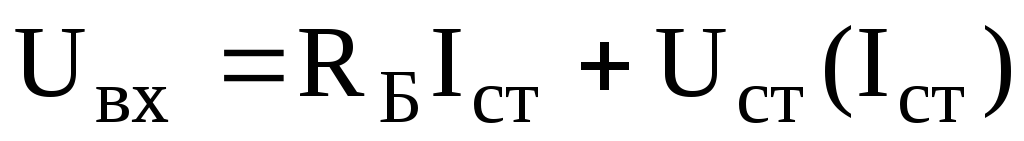
Напряжение 
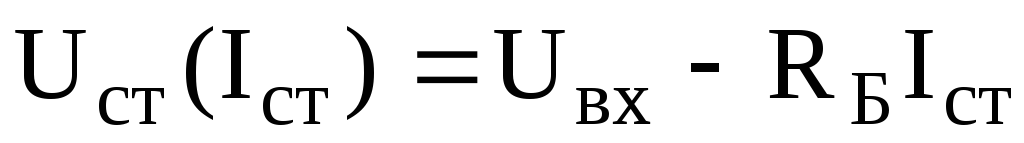
Графическое решение этого уравнения представлено на рис. 6.13. Правая часть уравнения (6.14) соответствует прямой, пересекающей ось напряжения в точке 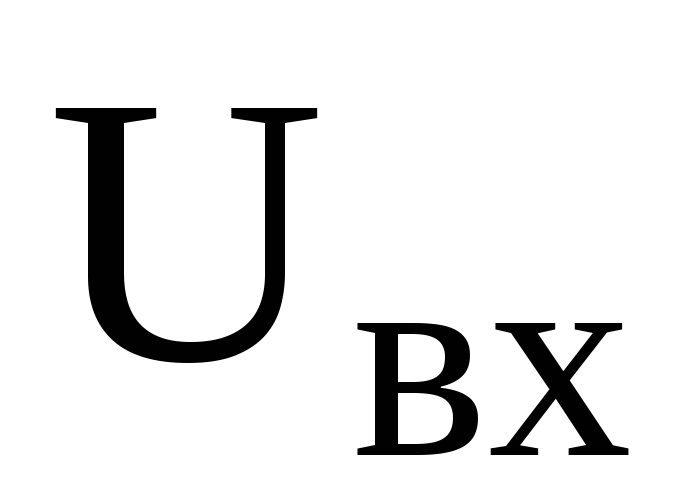

С помощью построений, представленных на рис. 6.13, можно проиллюстрировать стабилизирующее действие схемы на рис. 6.12,а. Пусть входное напряжение увеличивается на величину 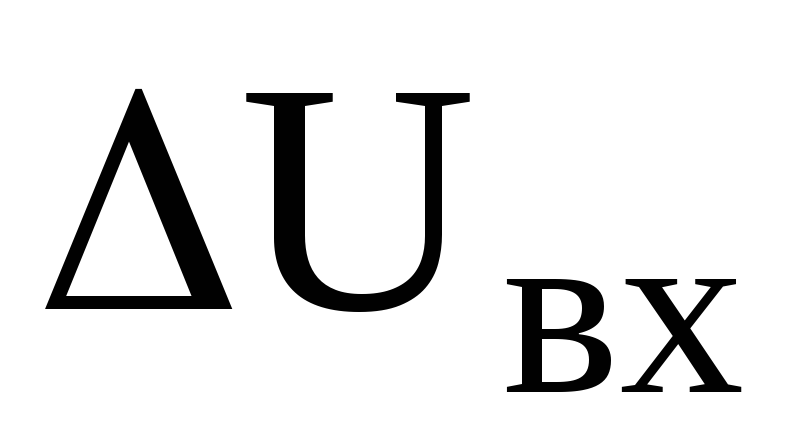
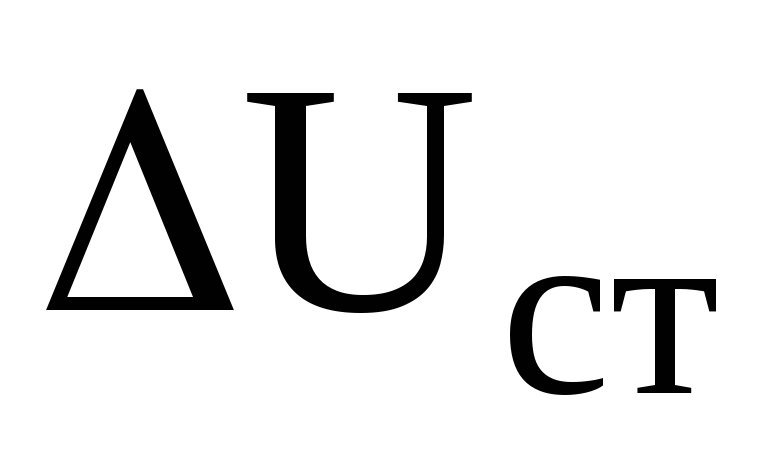
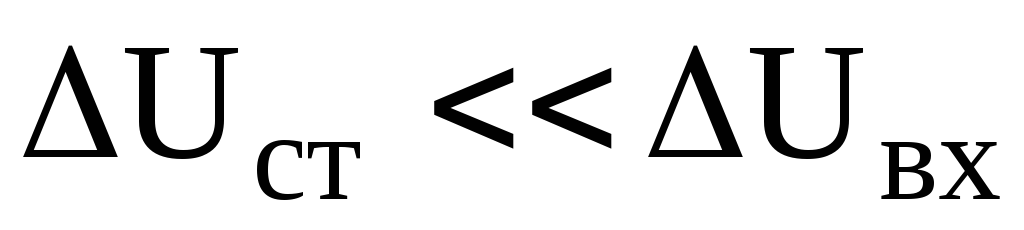
Количественным показателем качества стабилизации напряжения является коэффициент стабилизации, определяемый как отношение относительных изменений входного и выходного напряжений.
КСТ = 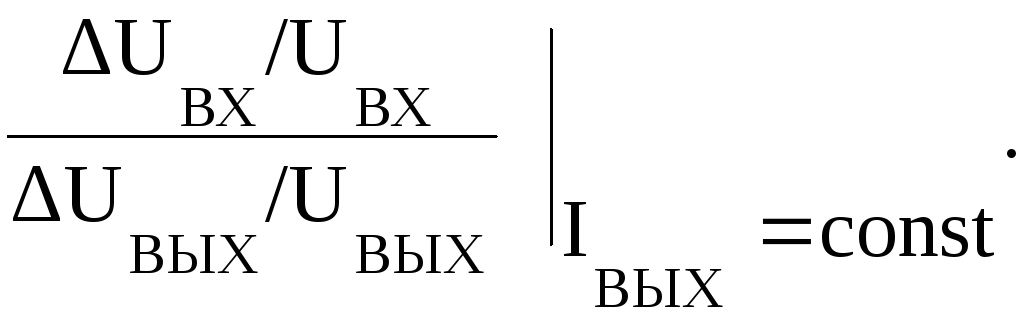
Величина этого коэффициента усиления для схемы на рис. 6.12,а может быть получено из рассмотрения подобных треугольников, получающихся при построении на рис. 6.13,а. Участок этого рисунка, обведенный окружностью, в увеличенном масштабе представлен на рис. 6.13,б. Величина изменения тока стабилитрона, обусловленная изменением входного напряжения, может быть выражена формулой
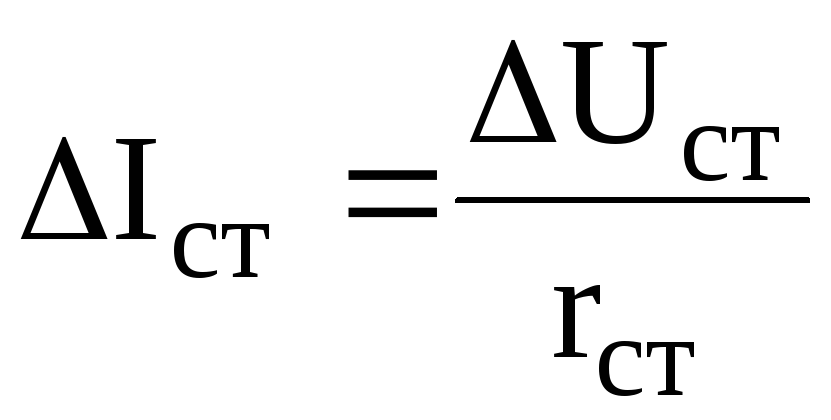
где 
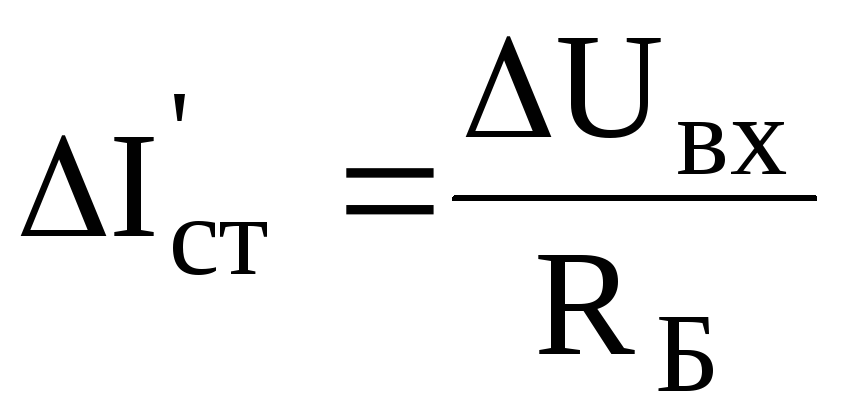
Из подобия треугольников на рис. 6.13,б следует:
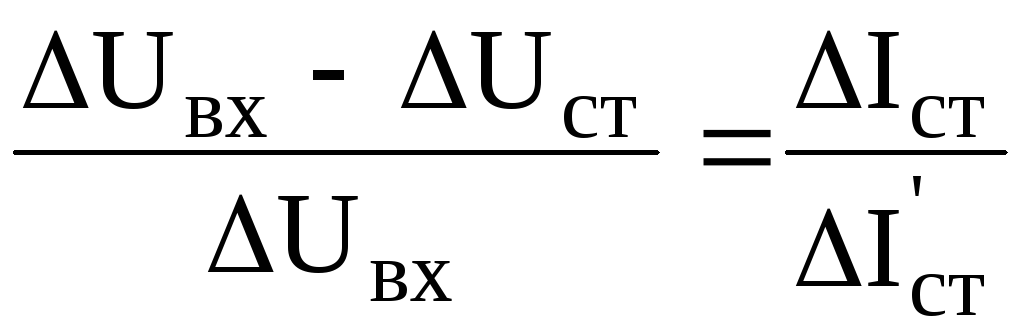
После подстановки в это уравнение соотношений (6.16) и (6.17) нетрудно получить:
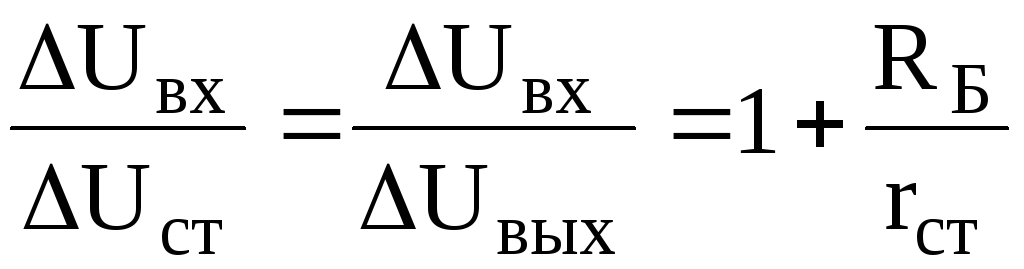
Откуда видно, что для обеспечения стабилизации выходного напряжения должно выполняться условие

Тогда коэффициент стабилизации согласно определению (6.15):
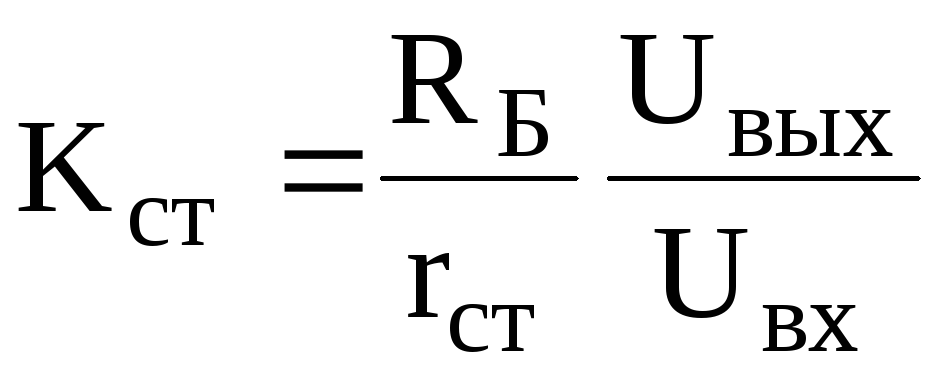
Для типовых полупроводниковых стабилитронов величина динамического сопротивления находится в пределах от единиц до нескольких сотен Ом. Величина коэффициента стабилизации, обеспечивающаяся схемой рис. 6.12,а, обычно не превышает 20÷40. Для получения более высокой стабильности напряжения необходимо использовать компенсационные стабилизаторы.