Что такое внешний угол треугольника каким свойством он обладает
Внешний угол треугольника – определение и свойство
Внешний угол треугольника редко используется при решении геометрических задач. Однако при этом свойства внешнего угла лучше знать, потому как задача на применение этих свойств рано или поздно попадется каждому ученику.
Внешний угол
Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равняется 180 градусам. Смежными углами зовутся углы, одна из сторон которых лежит на одной прямой, а вторая является общей.
Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых и смежных углов будет два.
Рис. 1. Внешние углы треугольника.
Итого в треугольнике получается 6 внешних углов.
Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.
Свойства внешних углов
Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.
Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:
Вычтем из первого выражения второе и получим:
d=в+с – вот и все доказательство.
Рис. 2. Рисунок к доказательству.
Есть еще несколько дополнительных свойств внешних углов:
Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.
Рис. 3. Внешний угол тупоугольного треугольника.
Что мы узнали?
Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.
Внешний угол
Внешний угол.
Внешний угол треугольника (понятие и определение):
Внешний угол треугольника или многоугольника – это угол, смежный с каким-нибудь внутренним углом этого треугольника или многоугольника.
Внешним углом треугольника при данной вершине называется угол, смежный с внутренним углом треугольника при этой вершине.
Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.
Рис.1. Внешний угол треугольника
Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно.
При каждой вершине треугольника имеются два внешних угла. Таким образом, у каждого треугольника существует 6 внешних углов.
Рис.2. Внешние углы треугольника
Теорема о внешнем угле треугольника:
Внешний угол треугольника равен сумме двух оставшихся внутренних углов треугольника, не смежных с этим внешним углом.
Рис.3. Внешний угол треугольника
Доказательство теоремы о внешнем угле треугольника следует из теоремы о сумме углов треугольника, равной 180°:
Теорема о внешнем угле треугольника используется тогда, когда пытаются вычислить меры неизвестных углов в геометрии, в задачах с многоугольниками, где используются треугольники.
Теорема о внешнем угле треугольника применима только к плоским треугольникам и не применима ни в сферической геометрии, ни в связанной с ней эллиптической геометрии (геометрии Римана).
Внешний угол треугольника: определение и свойство
Вы будете перенаправлены на Автор24
Основные определения
Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:
Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.
Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.
Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ
Теорема о сумме углов треугольника
Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:
Готовые работы на аналогичную тему
Приведём её доказательство.
Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Внешний угол треугольника
В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:
Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.
Докажем эту теорему.
Рассмотрим следующий рисунок:
Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ
Рассмотрим пример задачи на данную тему.
Решение. Сделаем рисунок:
Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ
Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.
Что такое внешний угол треугольника каким свойством он обладает
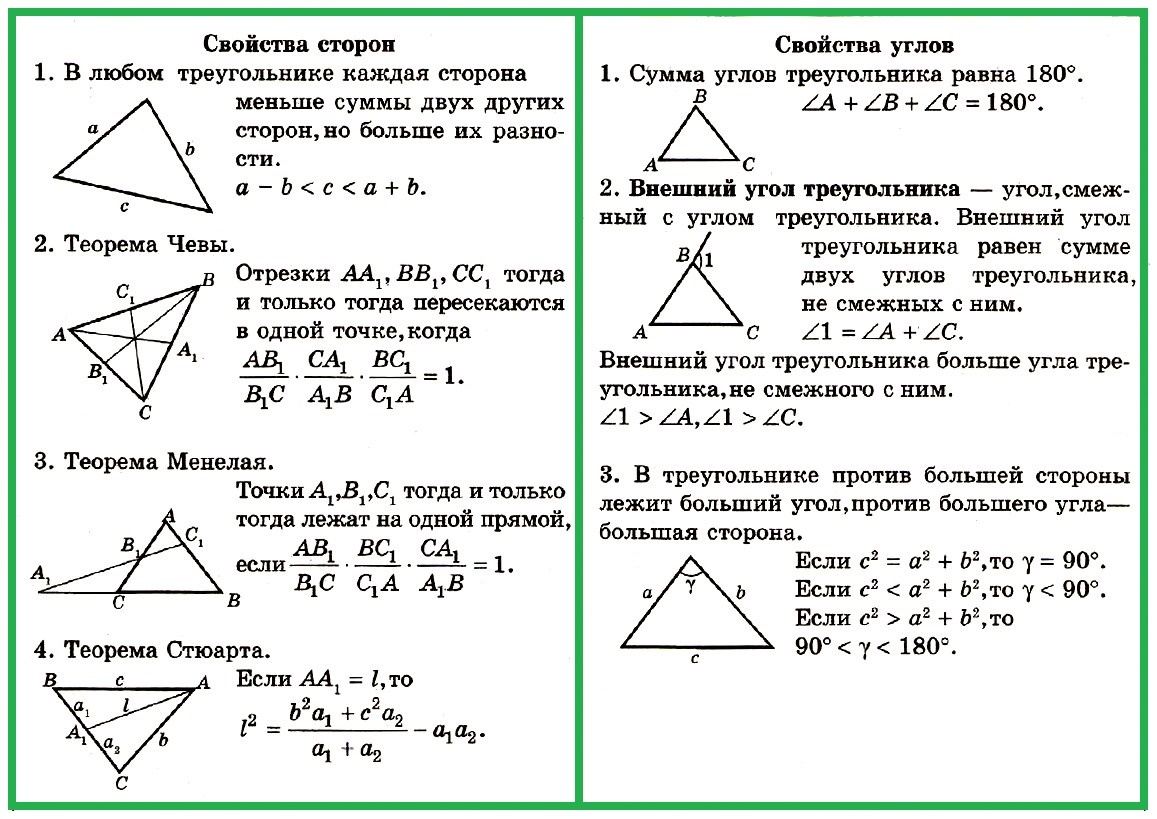
Свойства углов
1. Сумма углов треугольника равна 180°.
2. Внешний угол треугольника — угол, смежный с углом треугольника.
3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
4. Внешний угол треугольника больше угла треугольника, не смежного с ним.
5. В треугольнике против большей стороны лежит больший угол, против большего угла — большая сторона.
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
Задача № 1. Дано: AB = BC, CD AB, ∠ABC = 32. Найти: ∠ACD
Задача № 2. Дано: ABC, AB = BC, ∠DBC — внешний угол ABC, ∠DBC = 52. Найти: ∠BAC, ∠BCA.
Задача № 3. Дано: ABC, AB = BC, ∠C = 64, AD — биссектриса ∠A. Найти: ∠ADB.
Задача № 4. Дано: AD = DB, BK = KC, ∠BAD = 38, ∠BCK = 26. Найти: ∠BDK, ∠BKD, ∠DBK.
Это конспект по теме «Свойства сторон и углов треугольника». Выберите дальнейшие действия:
Каким свойством обладает внешний угол?
Как найти внешний угол в треугольнике?
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. ∠1 + ∠4 = 180°. Сумма внутренних углов углов любого треугольника тоже равна 180°, значит: ∠2 + ∠3 + ∠4 = 180°.
Какой угол называется внешним углом треугольника каким свойством он обладает?
Определение: Внешним углом треугольника называется угол, смежный с внутренним углом. Теорема (свойство внешнего угла): Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Как найти внешний угол треугольника при вершине С?
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Дано: ∆АВС, ∠1 — внешний угол при вершине С. Доказать: ∠1=∠А+∠В.
Как находить внешний угол при вершине?
Что такое внешний угол и как его найти?
Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно. Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.
Где находится внешний угол равнобедренного треугольника?
Внешний угол при основании равнобедренного треугольника на 90º больше половины внутреннего угла при его вершине.
Какой угол называется внешним углом треугольника Докажите что внешний угол треугольника равен сумме?
Какой угол называется внешним углом треугольника свойство внешнего угла?
Формулировка теоремы о внешнем угле треугольника
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине (внутренним углом) (рис. 2). Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Какой угол называется центральным углом окружности?
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра. Определение центрального угла: Центральный угол — это угол, вершина которого лежит в центре окружности. Центральный угол равен градусной мере дуги, на которую он опирается.
Как найти внешние углы равностороннего треугольника?
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. равен половине гипотенузы. равноугольный, а поэтому и равносторонний.
Что такое внешний и внутренний угол треугольника?
Как найти внешний угол правильного восьмиугольника?
Как найти внешний угол правильного многоугольника?
Свойства углов многоугольника
| Фигура | Формулировка теоремы |
|---|---|
| Углы n – угольника | Сумма углов многоугольника равна Посмотреть доказательство |
| Внешние углы n – угольника | Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° Посмотреть доказательство |
Сколько всего внешних углов в треугольнике?
Внешние углы треугольника. Итого в треугольнике получается 6 внешних углов. Нежелательно на рисунке строить два внешних угла при одной вершине одновременно.
Что такое внутренний угол?
Угол внутренний треугольника Угол, вершина которого совпадает с вершиной треугольника, а стороны проходят через две другие вершины. Например: угол ABC – это внутренний угол треугольника ABC при вершине B.