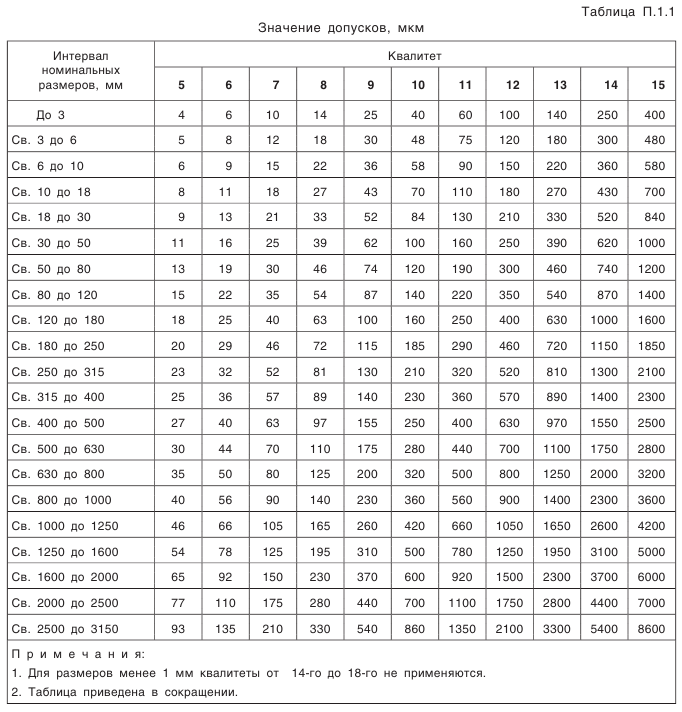
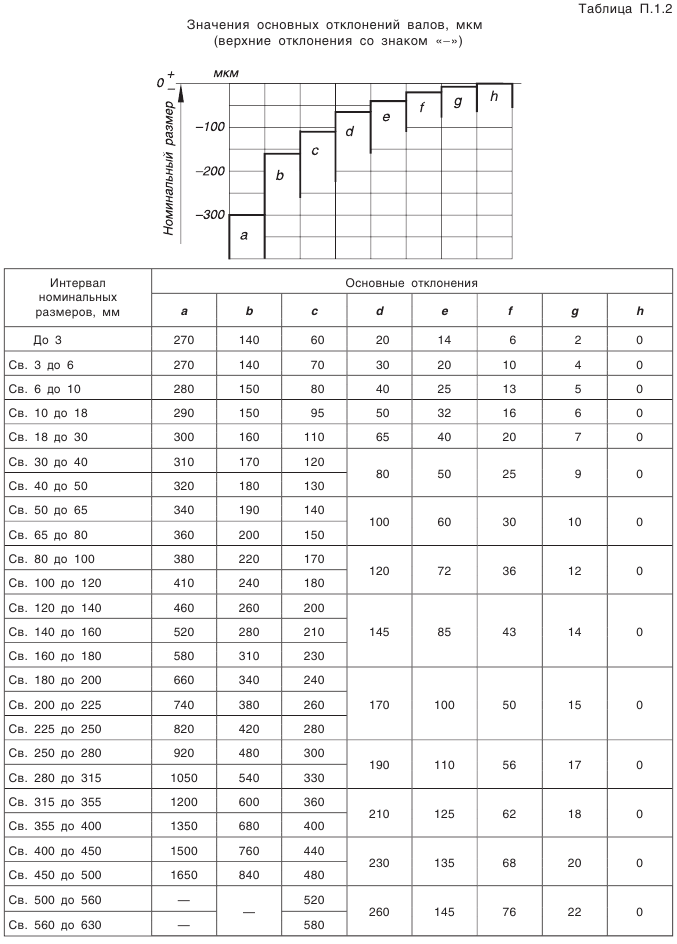
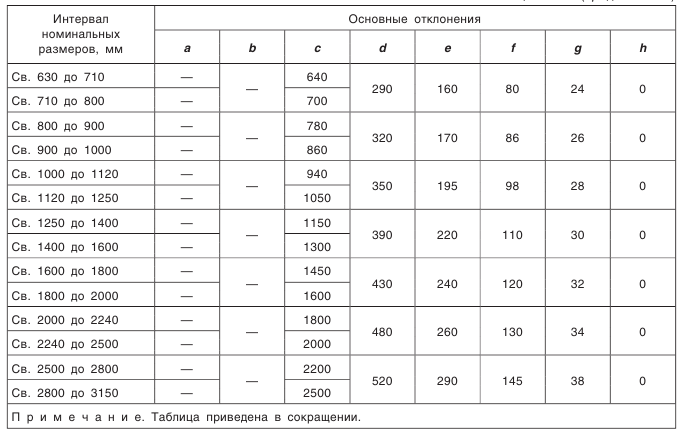
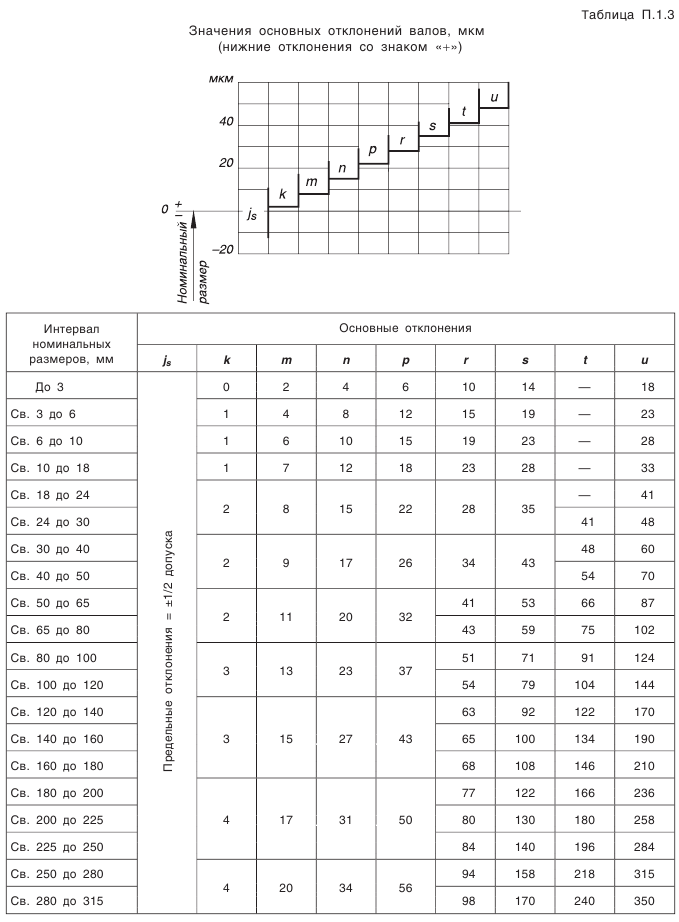
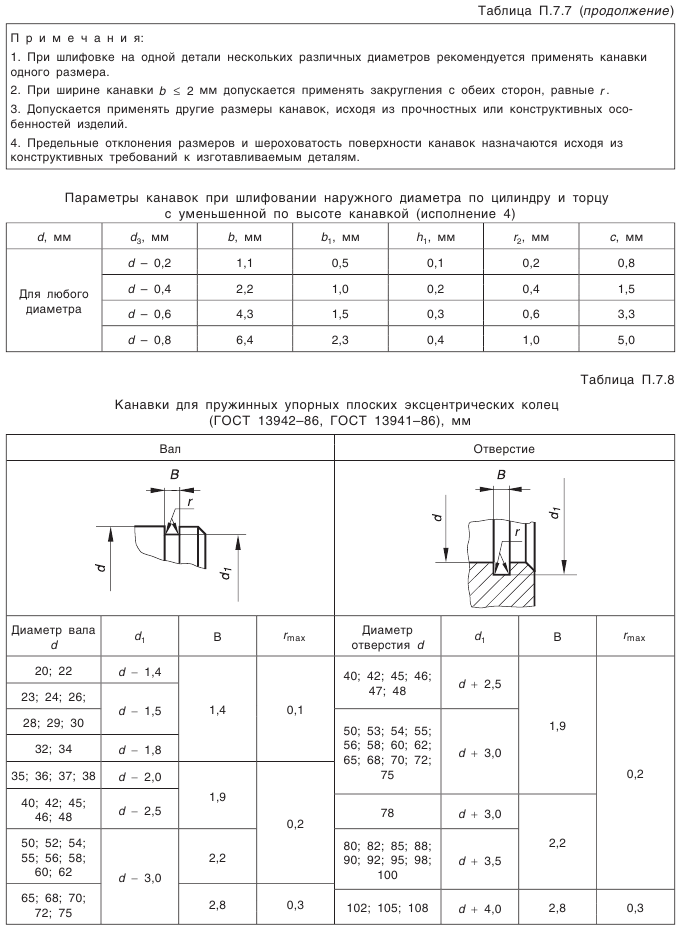
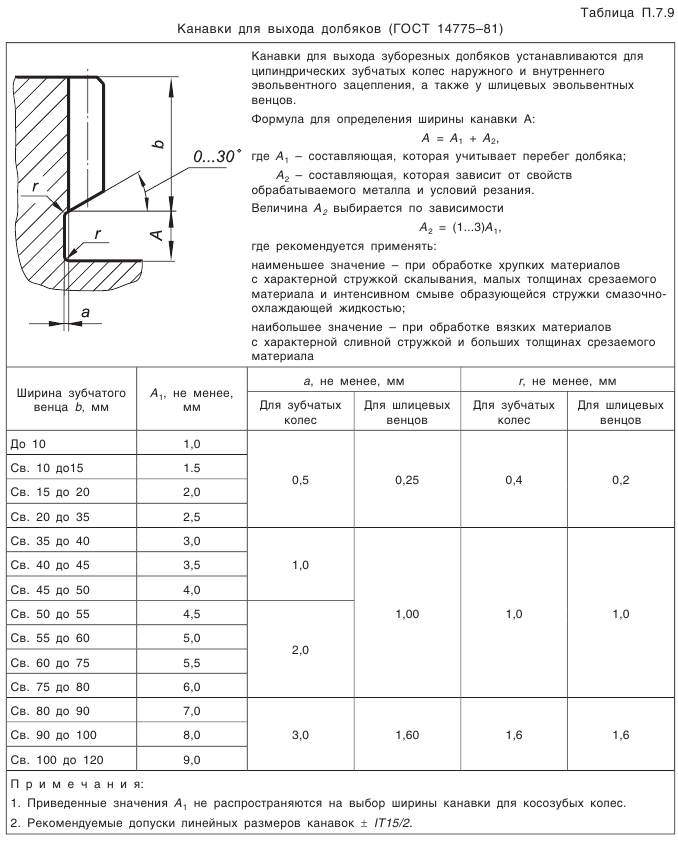
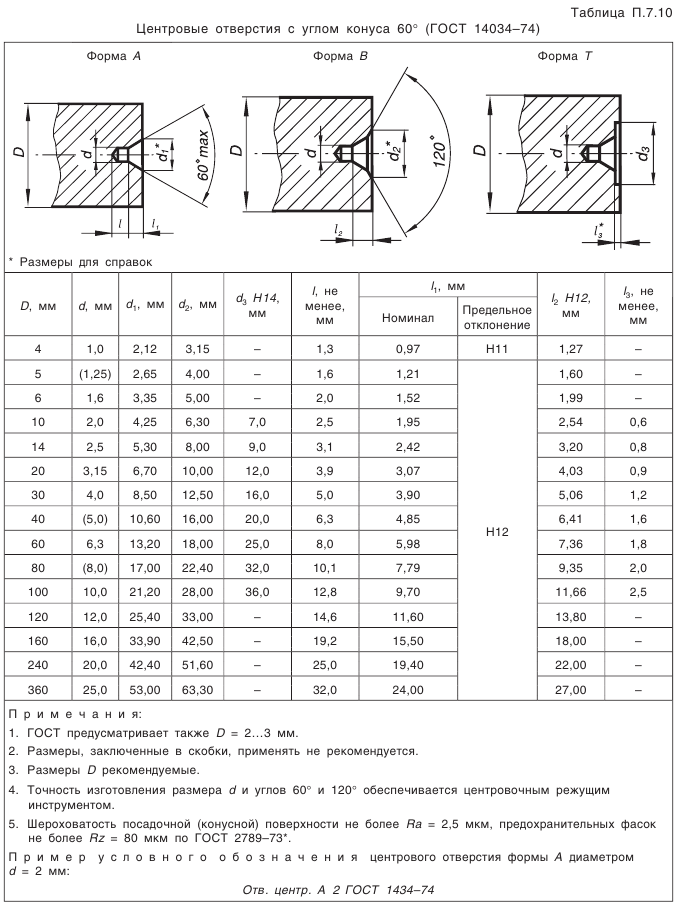
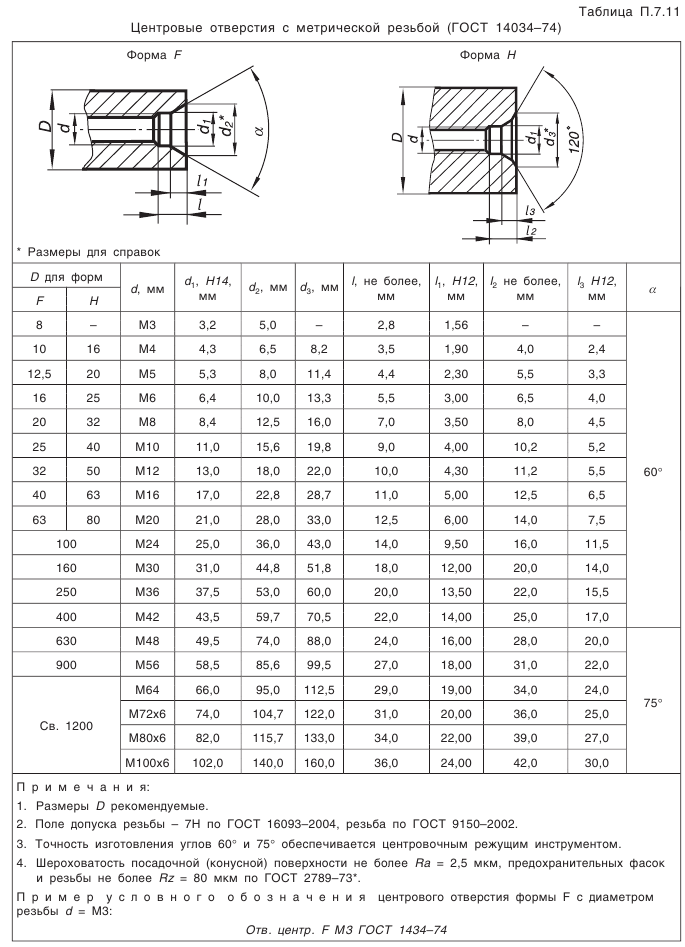
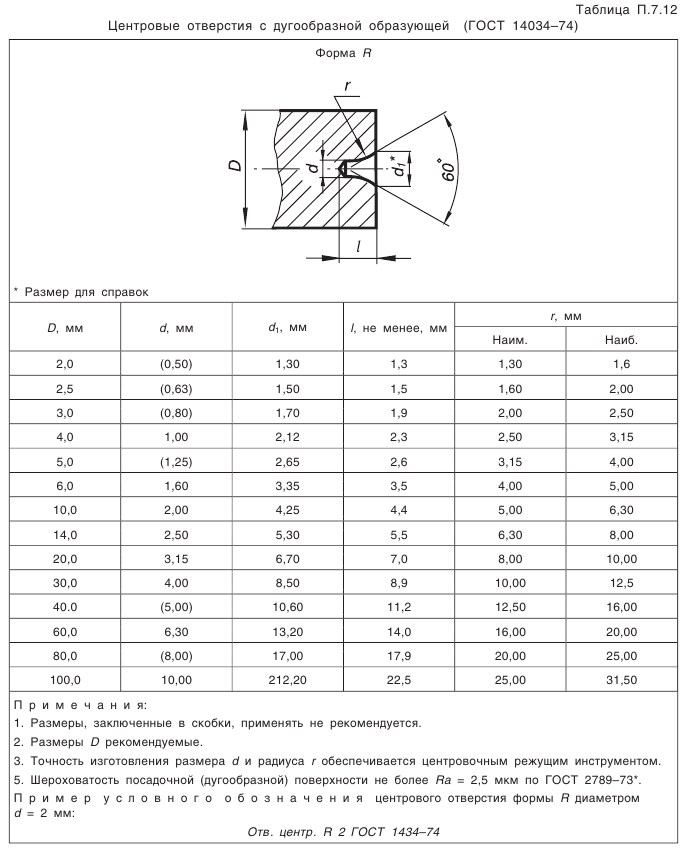
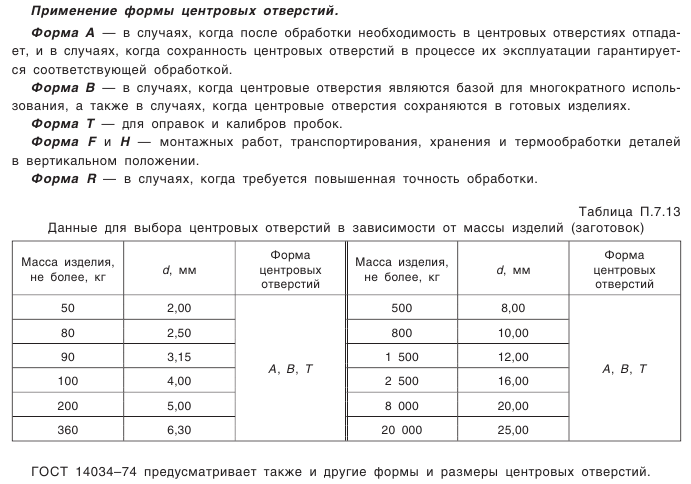
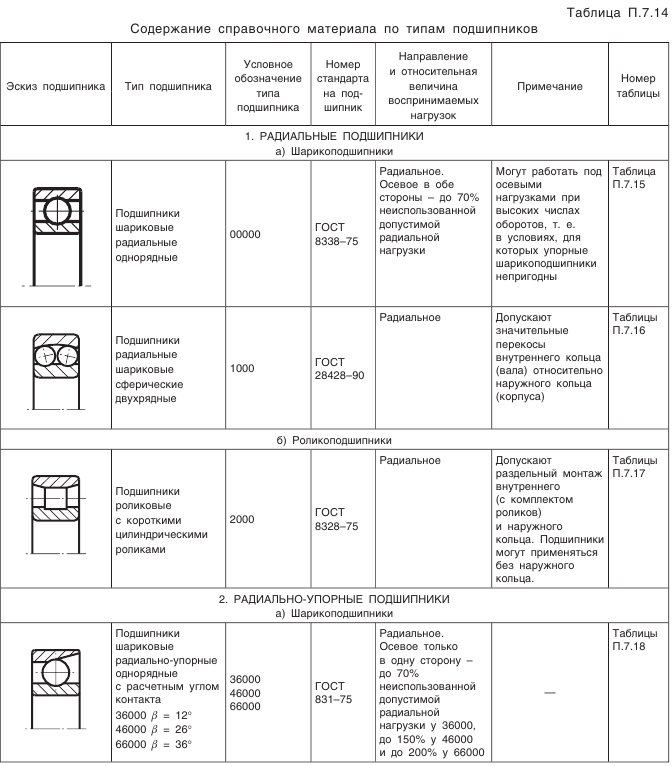
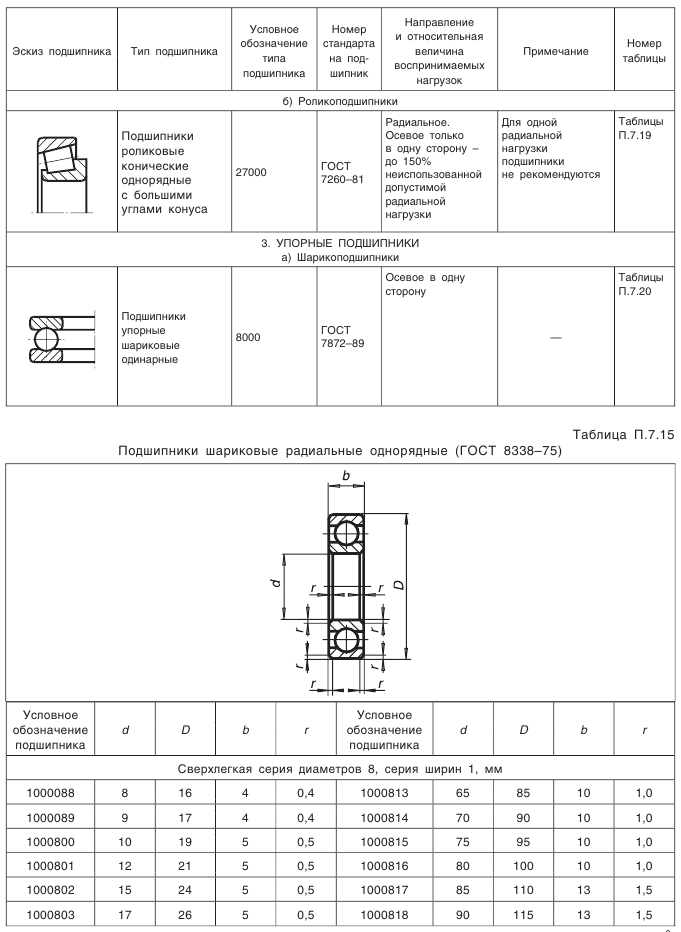
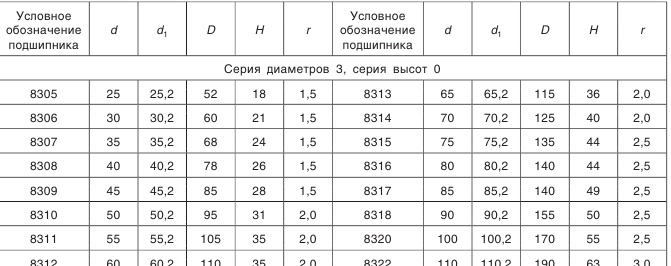
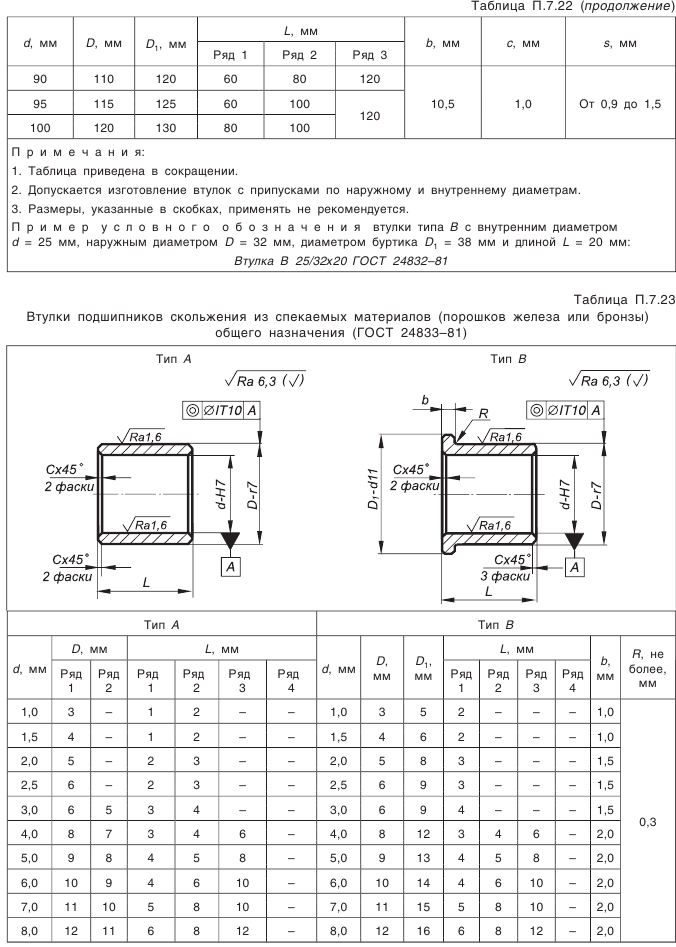
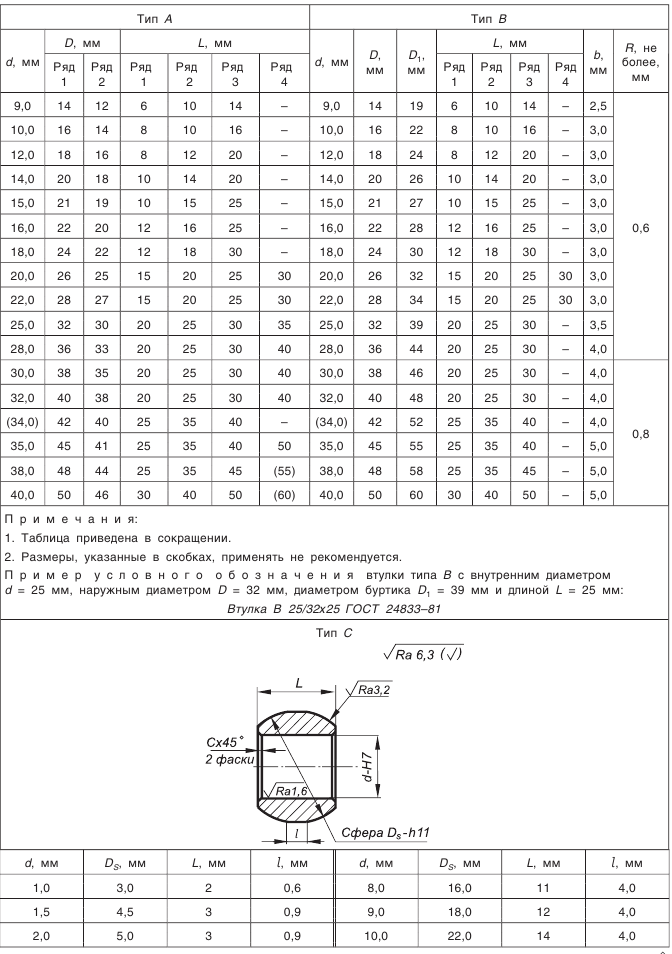
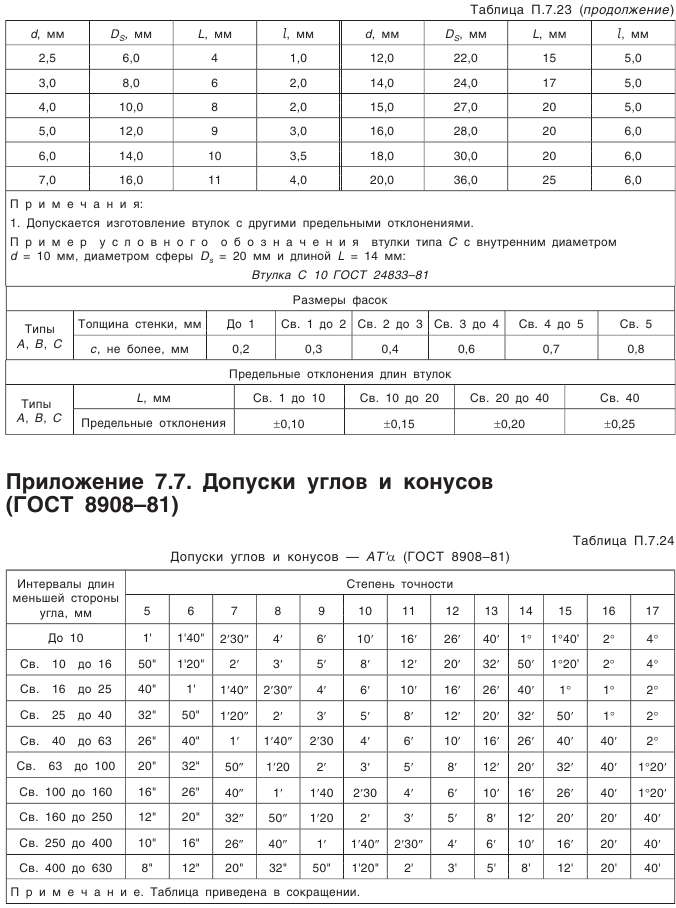
Что такое внешний окружной модуль
Детали машин
Конические зубчатые передачи
Общие сведения о конических зубчатых передачах
Конические передачи подразделяются не только по углу пересечения валов и осей зубчатых колес. Они бывают с прямыми и круговыми (спиралевидными) зубьями. Встречаются и конические передачи, у которых колеса выполнены с шевронными зубьями, но из-за сложности изготовления такие передачи широкого практического применения не нашли.
Прямозубые конические передачи имеют начальный линейный контакт в зацеплении, а передачи с круговыми зубьями – точечный контакт.
Основными преимуществами зубчатых колес с круговыми зубьями являются бόльшая несущая способность, относительная бесшумность и плавность работы. Недостаток – они сложнее в изготовлении, а, следовательно, дороже.
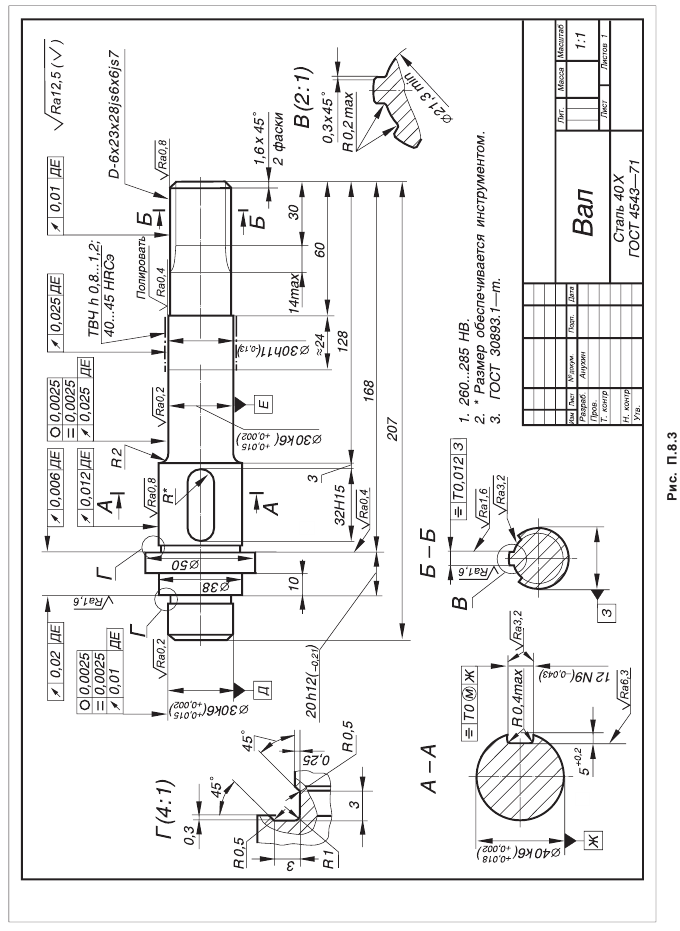
Нарезание кругового зуба производят резцовыми головками по методу обкатки (рис. 1). Угол наклона зуба βn в середине ширины зубчатого венца выбирают, учитывая плавность зацепления. Рекомендуется принимать βn = 35˚.
Сопряженные колеса с круговым зубом имеют противоположное направление линий зубьев – правое и левое, если смотреть со стороны вершины конуса. Шестерни выполняют с правым зубом, колеса – с левым (рис. 1 ).
В конических передачах шестерню, как правило, располагают консольно (рис. 2), при этом вследствие меньшей жесткости консольного вала и деформаций опор увеличивается неравномерность распределения нагрузки пол длине контактных линий в зацеплении. По этой причине конические колеса по сравнению с цилиндрическими работают с большим шумом.
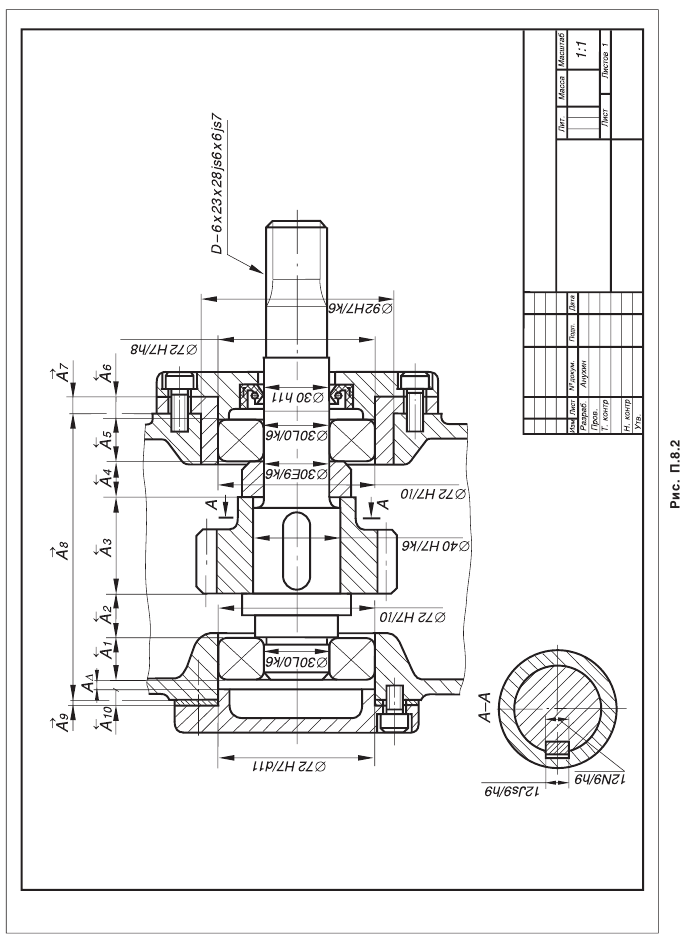
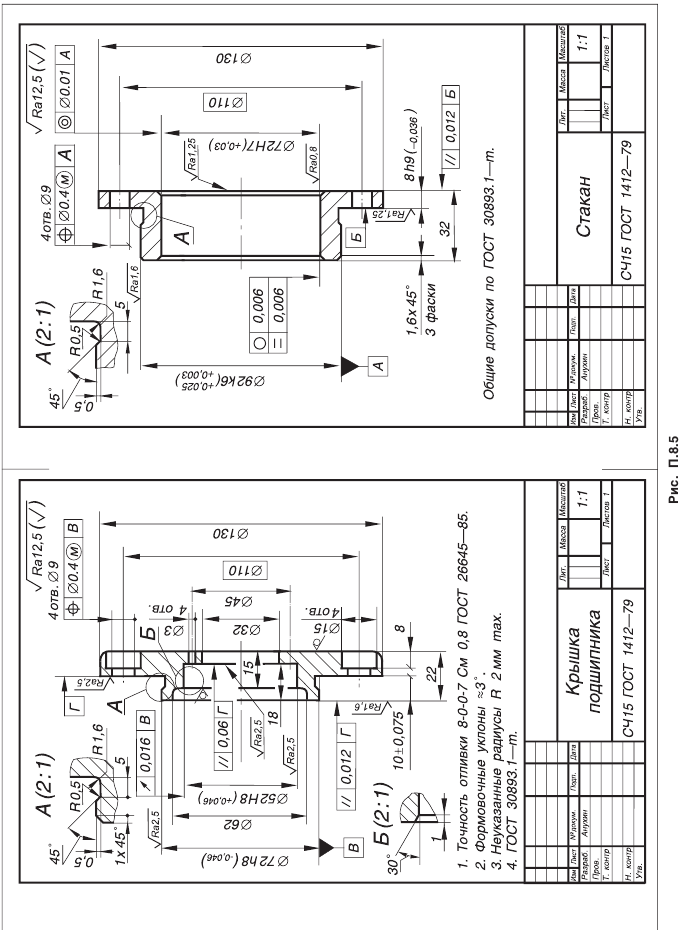
С целью снижения деформаций зубьев вал устанавливают на конических роликовых подшипниках, выдерживая соотношение l/l1 = 2,5 (рис. 2). Подшипники располагают в стакане для обеспечения возможности осевого перемещения узла конической шестерни при регулировании зацепления.
Передаточное число конической зубчатой передачи может быть определено из соотношений:
Для конической прямозубой передачи рекомендуемые значения передаточного числа u = 2…3, при колесах с круговыми зубьями – до 6,3.
Геометрия зацепления колес
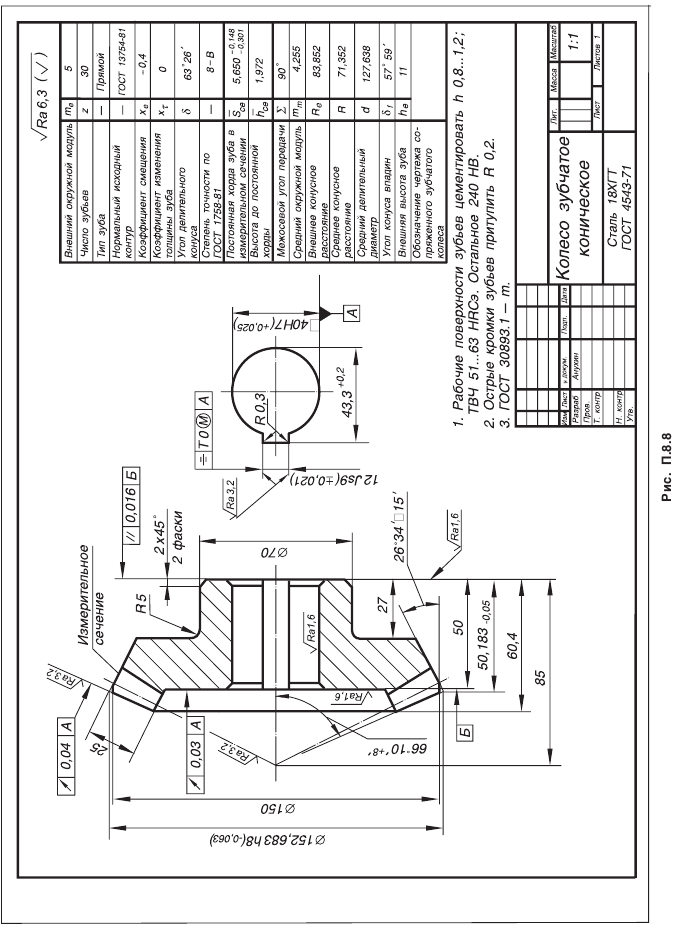
Эвольвентные зубья конического колеса профилируют на развертке дополнительного конуса, образующая которого перпендикулярна образующей делительного конуса. Дополнительные конусы можно построить для внешнего, среднего и внутреннего сечений зуба конического колеса.
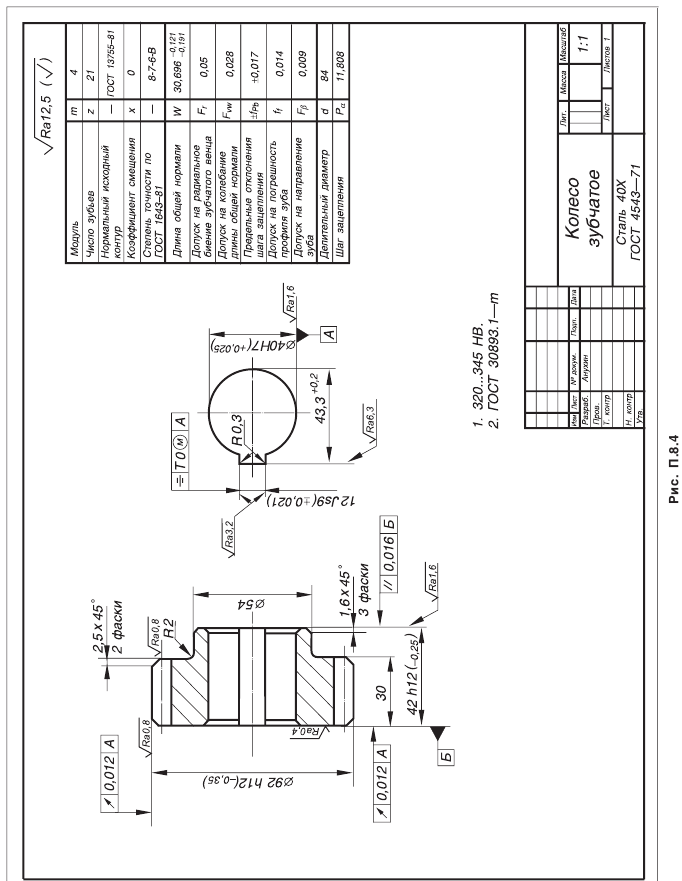
Ширина b венца зубчатого колеса ограничена двумя дополнительными конусами – внешним и внутренним.
Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют трех осевых форм (рис. 4).
Осевая форма I – нормально понижающиеся зубья.
Вершины делительного конуса и конуса впадин совпадают. Применяют для прямых зубьев, а также для круговых зубьев при m ≥ 2 мм и √(z1 2 + z2 2 ) = 20…100.
Осевая форма II – нормально сужающиеся зубья.
Вершина конуса впадин располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растет с увеличением расстояния от вершины. По этой форме одним инструментом можно обработать сразу обе поверхности зубьев колеса, что повышает производительность при нарезании зубчатых колес. Осевая форма II является основной для колес с круговыми зубьями. Применяют в массовом производстве.
Осевая форма III – равновысокие зубья.
Образующие конусов делительного, впадин и вершин параллельны. Высота зубьев постоянна по всей длине. Применяют для круговых зубьев при √(z1 2 + z2 2 ) ≥ 60 и для неортогональных передач с углом Σ me – для прямозубых колес, и mte – для колес с круговыми зубьями.
Внешний окружной модуль me или mte можно не округлять до стандартного, так как одним и тем же режущим инструментом можно нарезать колес с различными значениями модуля, лежащими в некотором непрерывном интервале.
Для повышения износостойкости и сопротивления зубьев заеданию конические зубчатые колеса выполняют с высотной модификацией., выравнивающей удельные скольжения зубьев шестерни и колеса. Коэффициенты смещения режущего инструмента хe1 для прямозубой шестерни и хn1 для шестерни с круговым зубом принимают по справочным таблицам.
Коэффициенты смещения для колес соответственно равны:
Для передач, у которых число зубьев z и передаточное число u отличаются от табличных значений, коэффициенты смещения хe1 и хn1 принимают с округлением в бόльшую сторону.
Основные геометрические соотношения конических зубчатых передач в соответствии с рисунком 4 приведены в таблице 1.
Таблица 1. Геометрические соотношения конических зубчатых передач.
Что такое внешний окружной модуль
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПЕРЕДАЧИ ЗУБЧАТЫЕ КОНИЧЕСКИЕ С ПРЯМЫМИ ЗУБЬЯМИ
Straight bevel gear pairs.
Calculation of geometry
Дата введения 1975-01-01
Постановлением Государственного комитета стандартов Совета Министров СССР от 28 марта 1974 г. N 718 срок действия установлен с 01.01.75
ПЕРЕИЗДАНИЕ. Май 1990 г.
Настоящий стандарт распространяется на зубчатые конические передачи с прямыми пропорционально понижающимися зубьями внешнего зацепления с внешним окружным модулем более 1 мм, с межосевыми углами от 10 до 170° и с прямолинейным профилем исходного контура, зубчатые колеса которых нарезаются методом обкатки зубострогальными резцами и парными зуборезными головками, а также методом копирования по шаблону.
Стандарт устанавливает метод расчета геометрических параметров зубчатой передачи, а также геометрических параметров зубчатых колес, приводимых на рабочих чертежах.
Стандарт не распространяется на конические зубчатые передачи с прямыми зубьями кругового профиля.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Принципиальная схема расчета геометрии приведена на чертеже.
1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-83 и ГОСТ 19325-73.
1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес, выделены в таблицах настоящего стандарта полужирным шрифтом.
1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.
1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду внешний торцовый профиль.
1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.
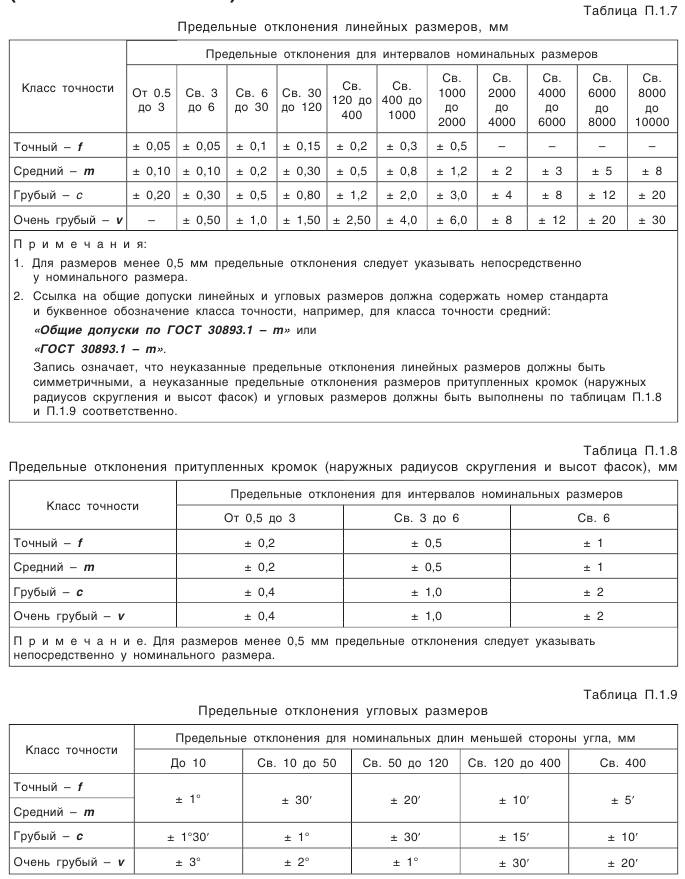
1.7. Вычисления по формулам стандарта и приложений к нему, за исключением случаев специально отмеченных, должны производиться со следующей точностью:
1.8. Пример расчета приведен в справочном приложении 4.
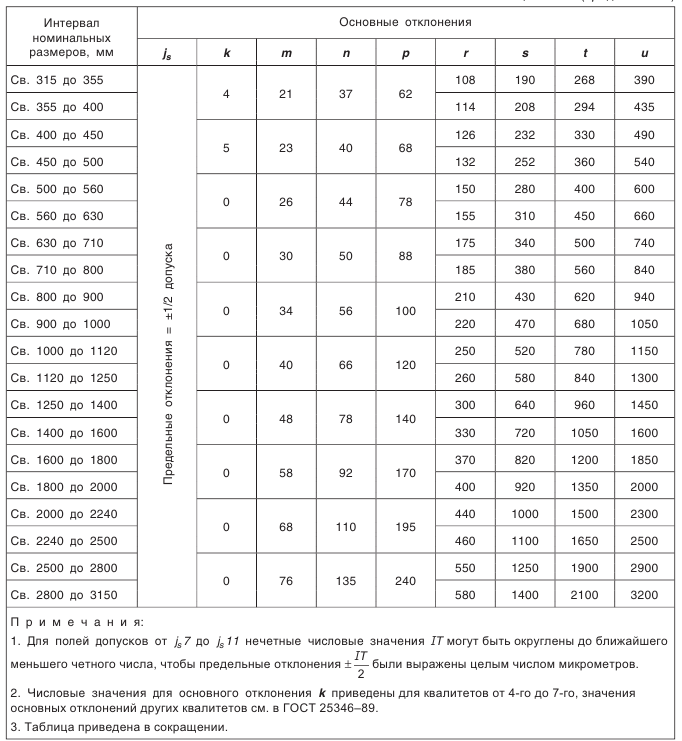
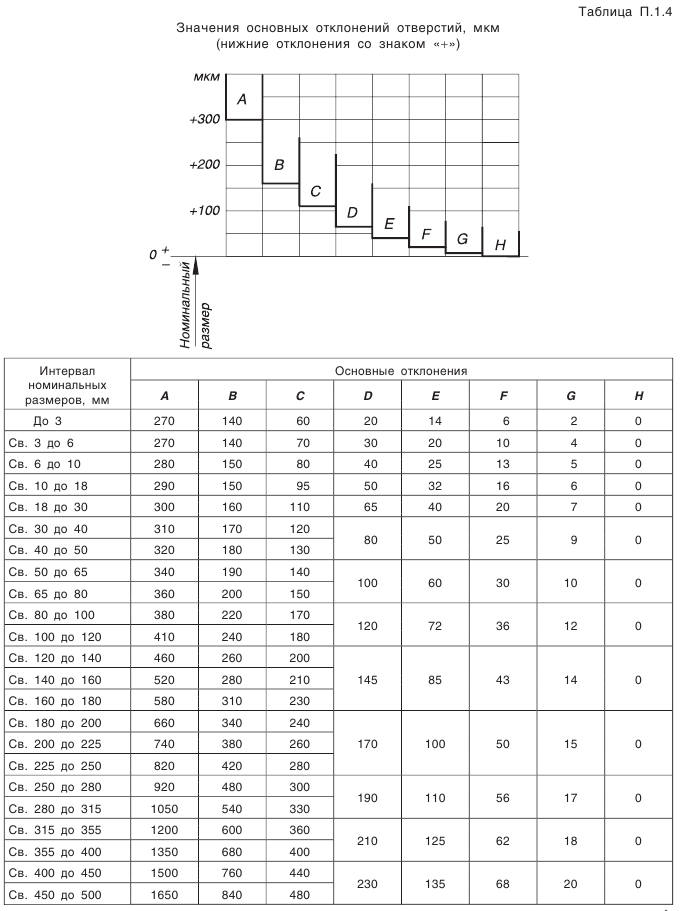
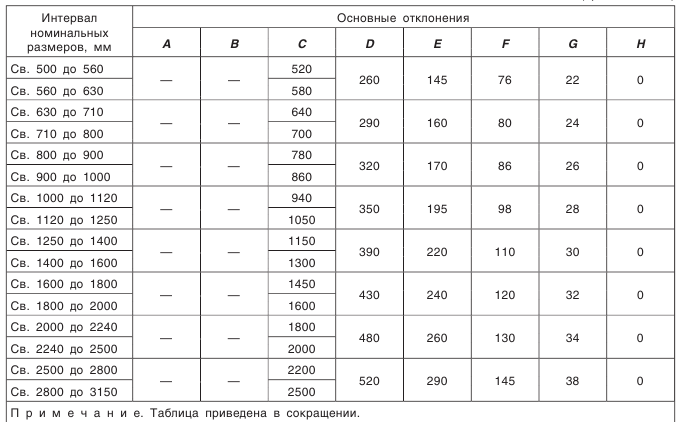
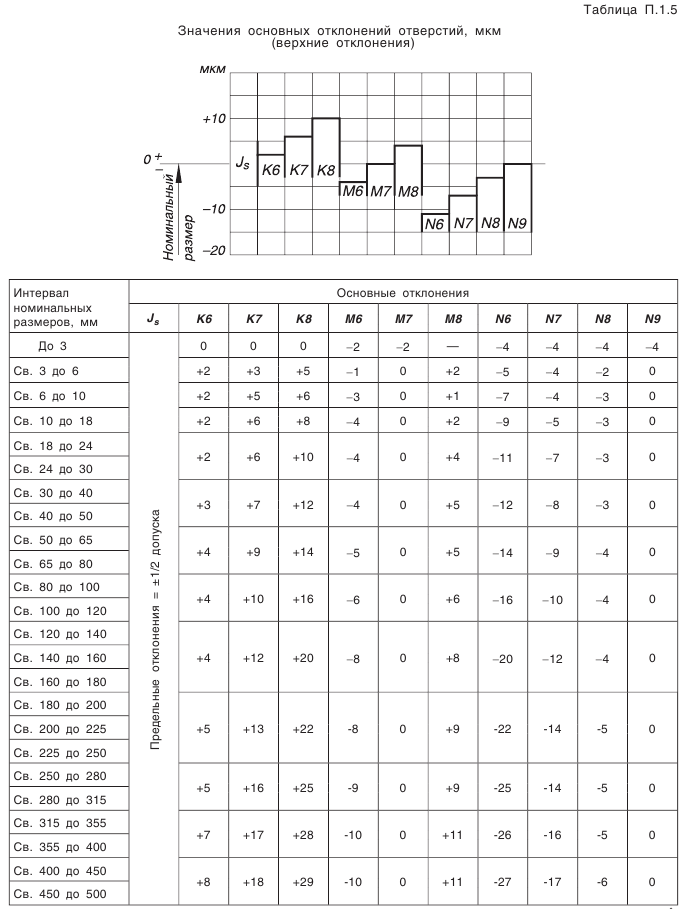
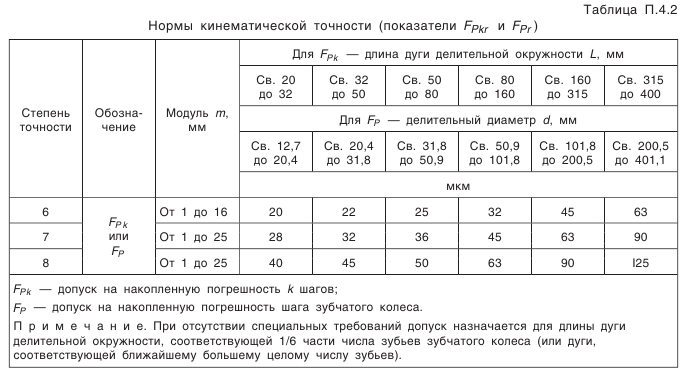
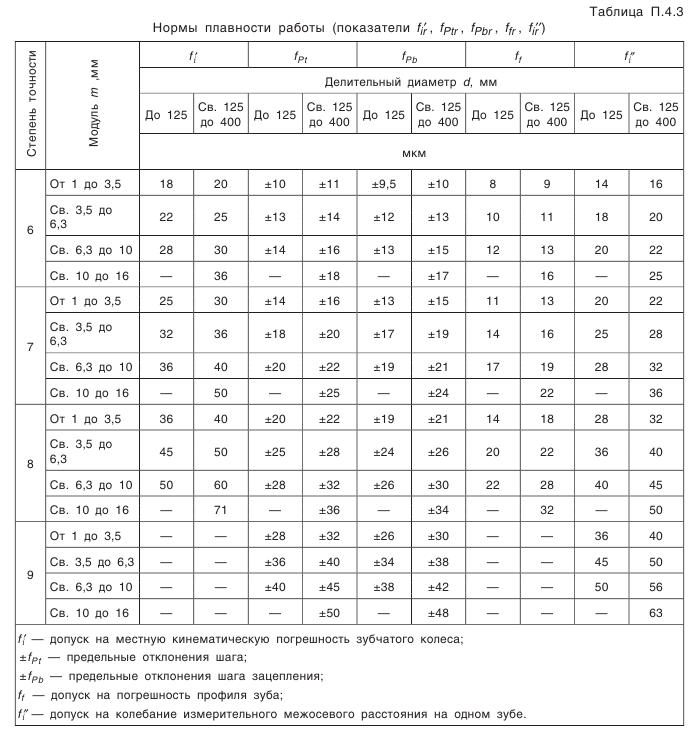
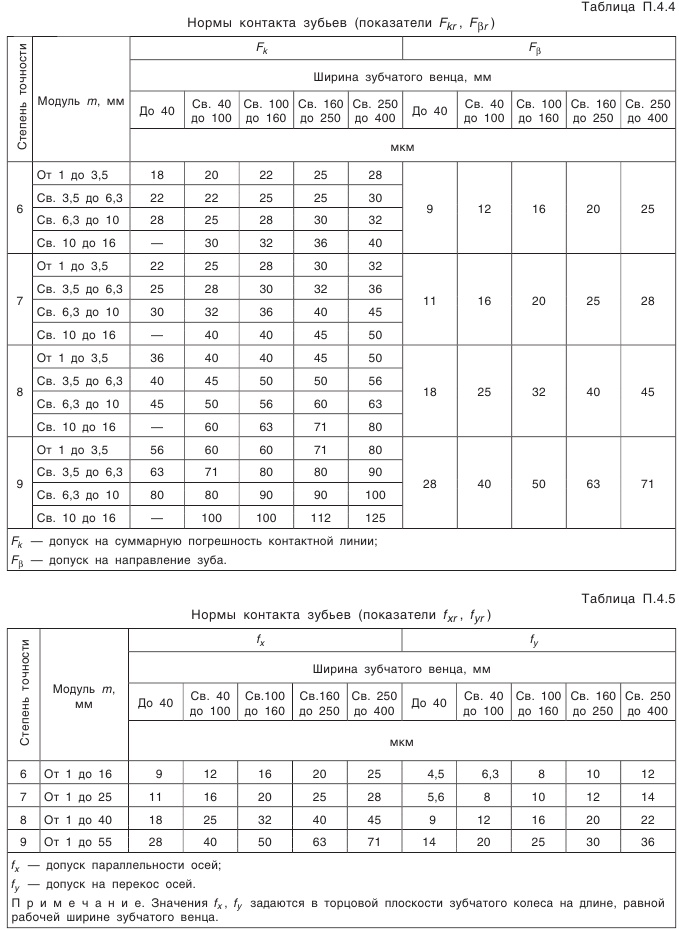
Выбор параметров зубчатого колеса, допусков размеров, формы, взаимного расположения и шероховатости поверхностей
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.


Not Found
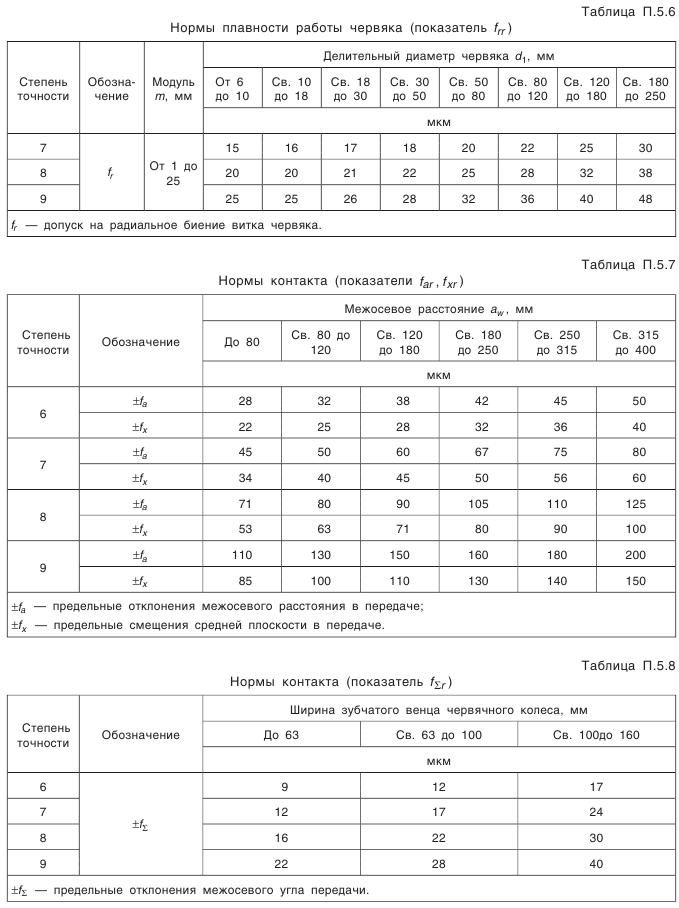
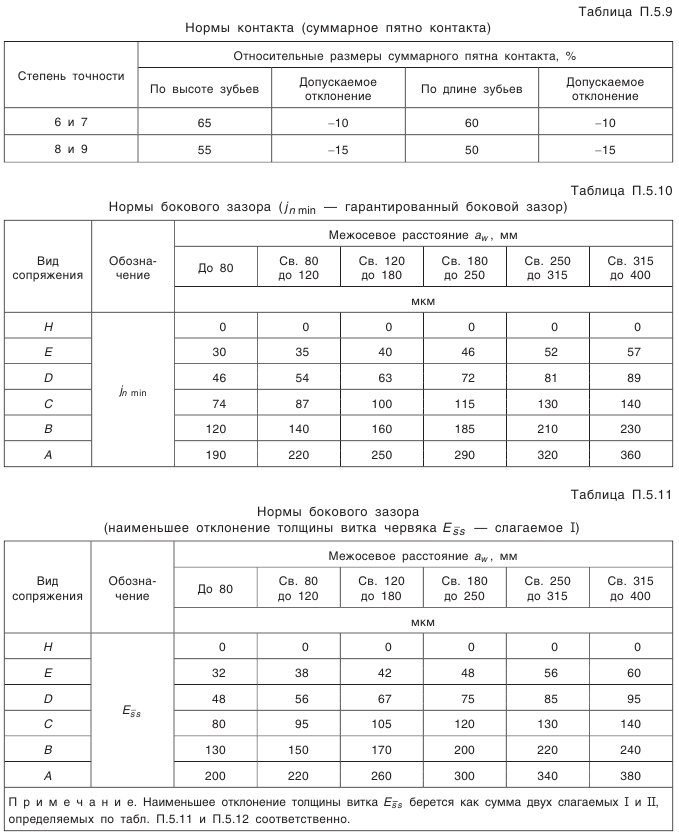
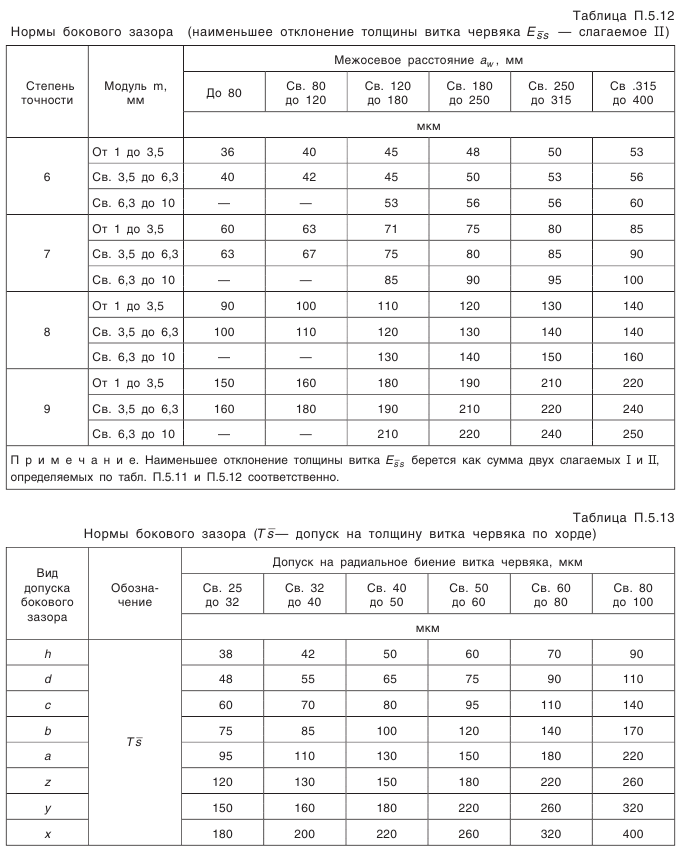
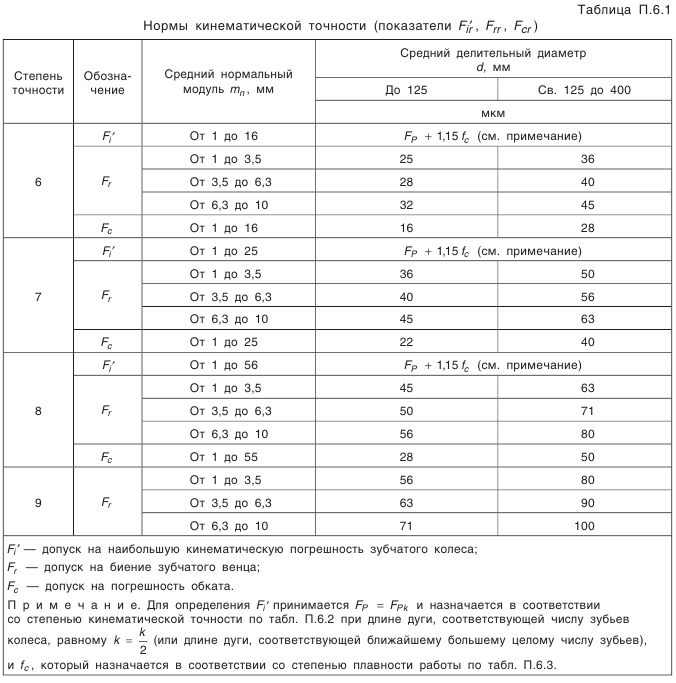
Глава IV ЗУБЧАТЫЕ И ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
Цилиндрические зубчатые передачи
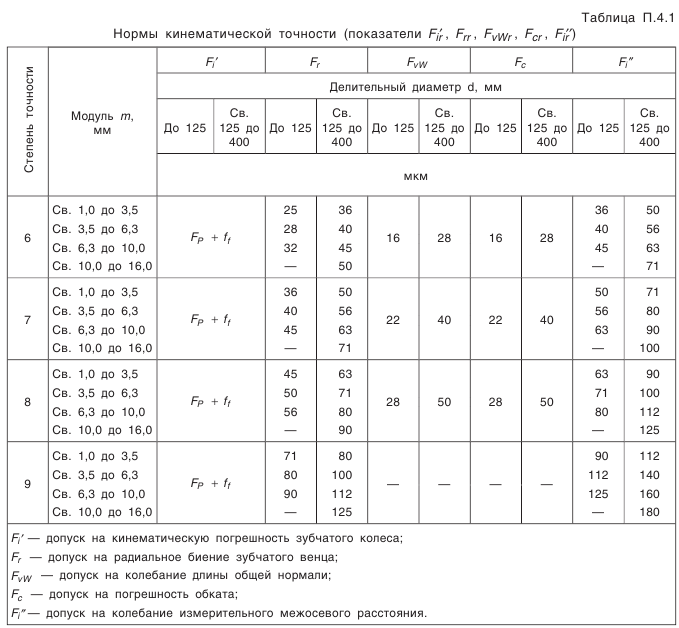
Термины и обозначения приведены в табл. 1, определения терминов см. ГОСТ 16530—83 и 16531-83.
1. Термины и обозначения цилиндрических зубчатых передач
Рис. 1. Исходный контур зубчатых цилиндрических колес эвольвентного зацепления то ГОСТ 13755—81 и конических колес с прямыми зубьями то ГОСТ 13754— 81
Шестерня — зубчатое колесо передачи с меньшим числом зубьев, колесо — с большим числом зубьев. При одинаковом числе зубьев зубчатых колес передачи шестерней называют ведущее зубчатое колесо, а колесом — ведомое. Индекс 1 — для величин, относящихся к шестерне, индекс 2 — относящихся к колесу. Индекс n
— для величин, относящихся к нормальному сечению,
t
— к окружному (торцовому) сечению. В тех случаях, когда не может быть разночтения и неясности, индексы
n
и
t
можно исключить. Термины параметров нормального исходного контура и нормального исходного производящего контура, выраженных в долях модуля нормального исходного контура, образуют добавлением слова «коэффициент» перед термином соответствующего параметра. Обозначения коэффициентов соответствуют обозначениям параметров с добавлением знака «*», например коэффициент радиального зазора пары исходных контуров
с*.Модули (по ГОСТ 9563—60).
Стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает: для цилиндрических колес — значения нормальных модулей; ддя конических колес — значения внешних окружных делительных модулей. Числовые значения модулей:
| Ряд1 | РЯД 2 | Ряд1 | Ряд 2 | Ряд1 | Ряд 2 | Ряд1 | Ряд 2 |
| 1 | 1,125 | — | — | 5 | 5,5 | 12 | 14 |
| 1,25 | 1,375 | 2,5 | 2,75 | 6 | 7 | 16 | 18 |
| 1,5 | 1,75 | 3 | 3,5 | 8 | 9 | 20 | 22 |
| 2 | 2,25 | 4 | 4,5 | 10 | 11 | 25 | 28 |
| 32 | 36 |
Под исходным контуром колес (рис. 1) подразумевают контур зубьев рейки в нормальном к направлению зубьев сечении. Радиальный зазор
с
= 0,25
m
, радиус кривизны переходной кривой зуба
рf
= 0,4
m.
Допускается увеличение радиуса р
f
, если это не нарушает правильности зацепления, и увеличение
с
до 0,35
m
при обработке колес долбяками и шеверами и до 0,4
m
при шлифовании зубьев. Для цилиндрических колес внешнего зацепления при окружной скорости более указанной в табл. 2 применяют исходный контур с модификацией профиля головки зуба (рис. 2). При этом линия модификации — прямая, коэффициент модификации
h
*g должен быть не более 0,45, а коэффициент глубины модификации ∆* — не более 0,02. Рекомендуемые значения коэффициента ∆* приведены в табл. 3.
Основные элементы
зубчатого зацепления указаны на рис. 3 и 4 в соответствии с обозначением по табл. 1.
Смещение колес зубчатых передач с внешним зацеплением.
Чтобы повысить прочность зубьев на изгиб, снизить контактные напряжения на их поверхности и уменьшить износ за счет относительного скольжения профилей, рекомендуется производить смещение инструмента для цилиндрических (и конических) зубчатых передач, у которых
Z1
≠
Z2
. Наибольший результат достигается в следующих случаях:
Рис. 2. Исходный контур с профильной модификацией
2. Окружная скорость колес в зависимости от их точности
| Тип колес | Окружная скорость в м/с при степени точности колеса по ГОСТ 1643-81 | ||
| 6 | 7 | 8 | |
| Прямозубые | 10 | 6 | 4 |
| Косозубые | 16 | 10 | 6 |
3. Коэффициент глубины модификации
∆
* в зависимости от модуля и степени точности
| Модуль m , мм | Степень точности по нормам плавности работы по ГОСТ 1643-81 | ||
| 6 | 7 | 8 | |
| До 2 | 0,010 | 0,015 | 0,020 |
| Св. 2 до 3,5 | 0,009 | 0,012 | 0,018 |
| » 3,5 » 6,3 | 0,008 | 0,010 | 0,015 |
| » 6,3 » 10 | 0,006 | 0,008 | 0,012 |
| » 10 » 16 | 0,005 | 0,007 | 0,010 |
| » 16 » 25 | — | 0,006 | 0,009 |
| »25 » 40 | — | — | 0,008 |
1) при смещении передач, у которых шестерня имеет малое число зубьев ( Z1
Читайте также: Развальцовка труб: тонкости технологии и основные инструменты
Рис. 5. Положение производящего реечного контура относительно заготовки:
номинальное;
б —
с отрицательным смещением;
в —
с положительным смещением
Рис. 6. График для определения нижнего предельного значения
Z1в зависимости отZ2, при которых εa
=1,2 (x1=х2=0,5)
Рис. 7. График для определения Хmin
(округляется до ближайшего большего целого числа)
Примеры. 1. Дано: z = 15; ß
= 0. По графику определяем
xmin
= 0,12 (см. штриховую линию). 2. Дано:
х = 0,ß
= 30 °. По графику определяем наименьшее число зубьев
Zmin
= 12 (см. штриховую линию)
Рис. 8. Влияние смещения исходного контура на геометрию зубьев
Рис. 9. Зацепление (в сечении, параллельном торцовому) зубчатого колеса со смещением с исходной производящей рейкой
Если исходная производящая рейка в станочном зацеплении смещена из номинального положения и установлена так, что ее делительная прямая не касается делительной окружности нарезаемого колеса, то в результате обработки получится колесо, нарезанное со смещением исходного контура (по старой терминологии — корригированное колесо).
4. Коэффициенты смещения у зубчатых колес прямозубой передачи
| Коэффициент смещения | Область применения | |||
| у шестерни x1 | у колеса x2 | |||
| 0 | 0 | Межосевое расстояние aw задано равным 0,5(z1 + z2) | Кинематические передачи | z1≥17 |
| 0,3 | -0,3 | 12 ≤ z1 30 | ||
| 0,5 | 0,5 | 10 ≤ z1 ≤ 30. В пределах 10 ≤ z1 ≤ 16 нижнее предельное значение z1 определяется по графику (рис.6) | ||
5. Коэффициент смещения у зубчатых колес косозубой и шевронной передач







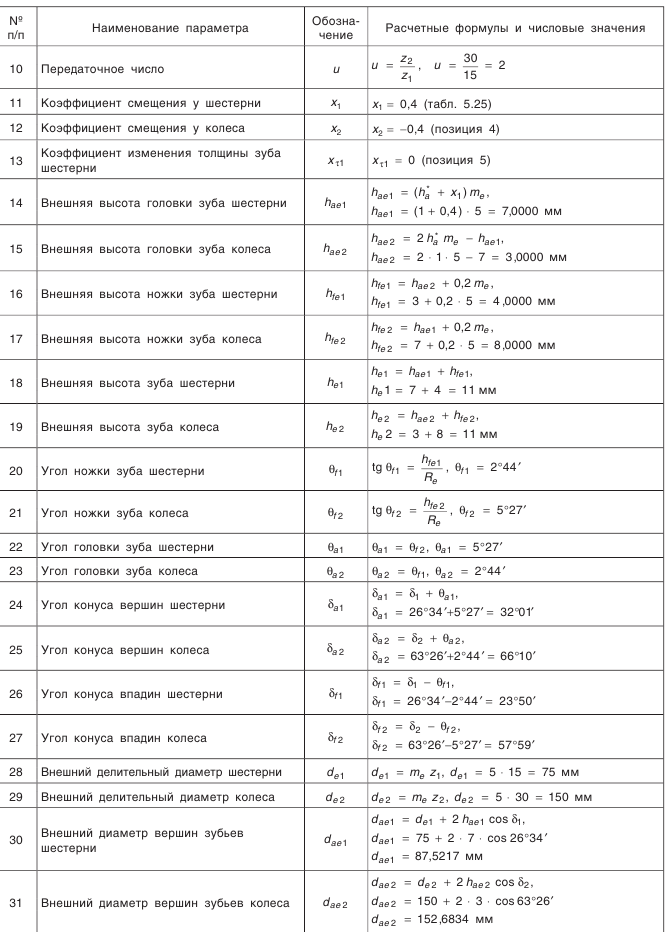
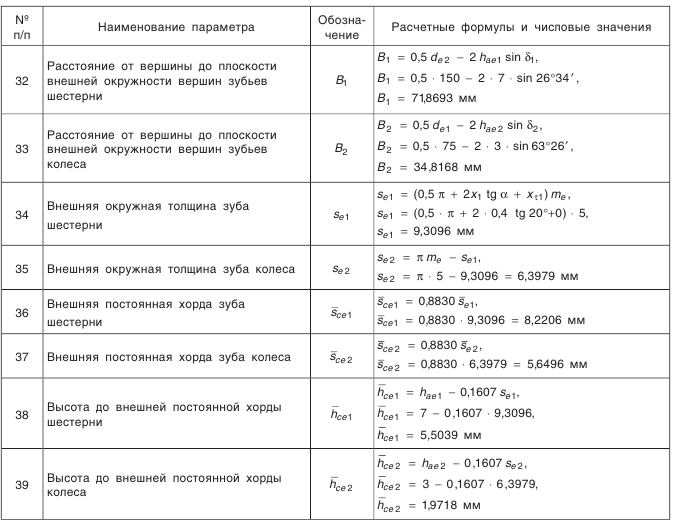
 конической передачи с прямыми зубьями показан в табл. 5.21.
конической передачи с прямыми зубьями показан в табл. 5.21.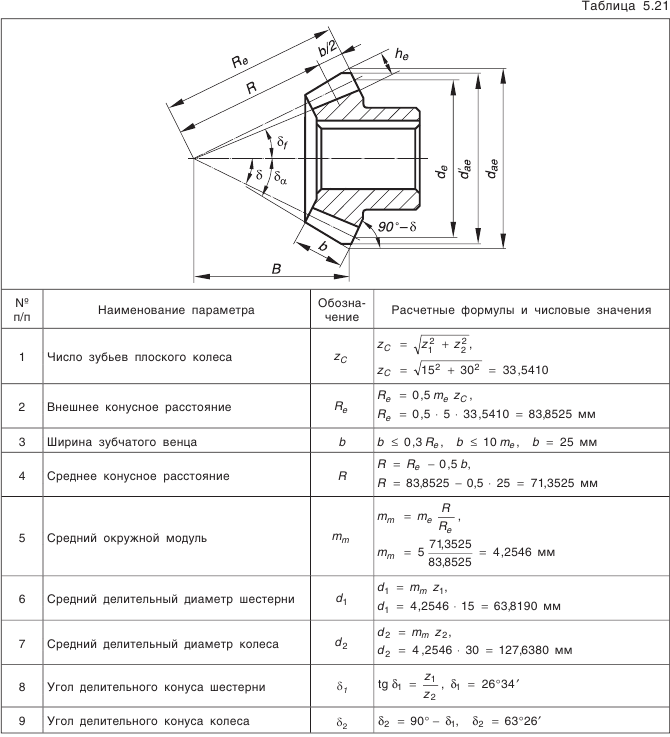
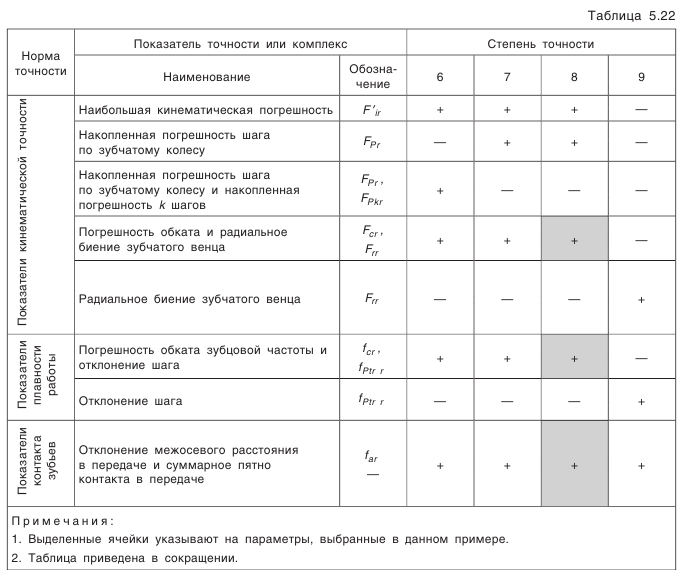
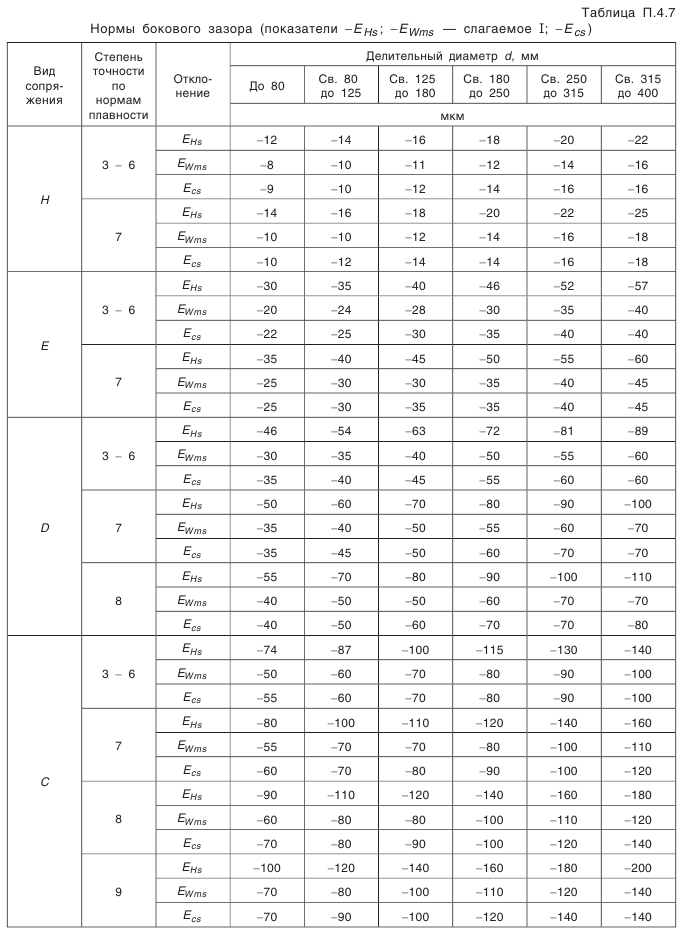
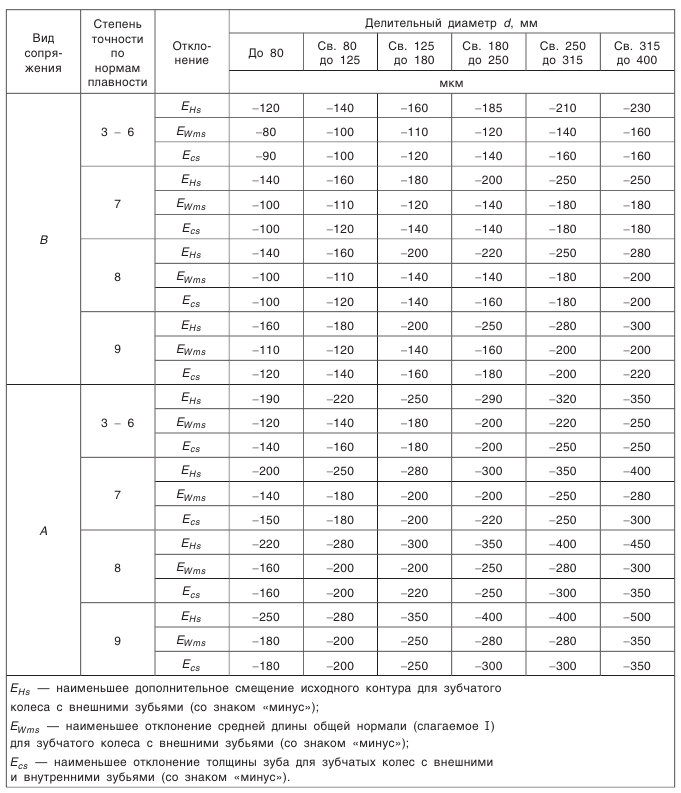
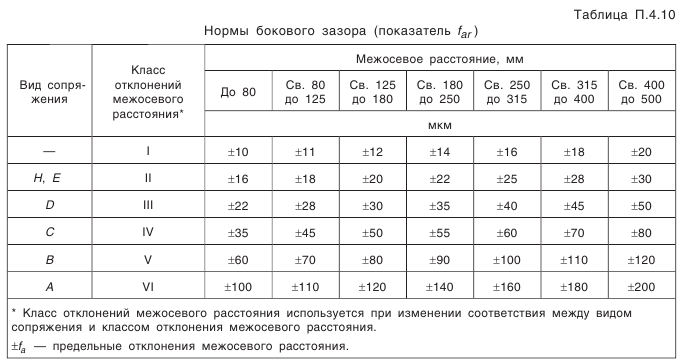
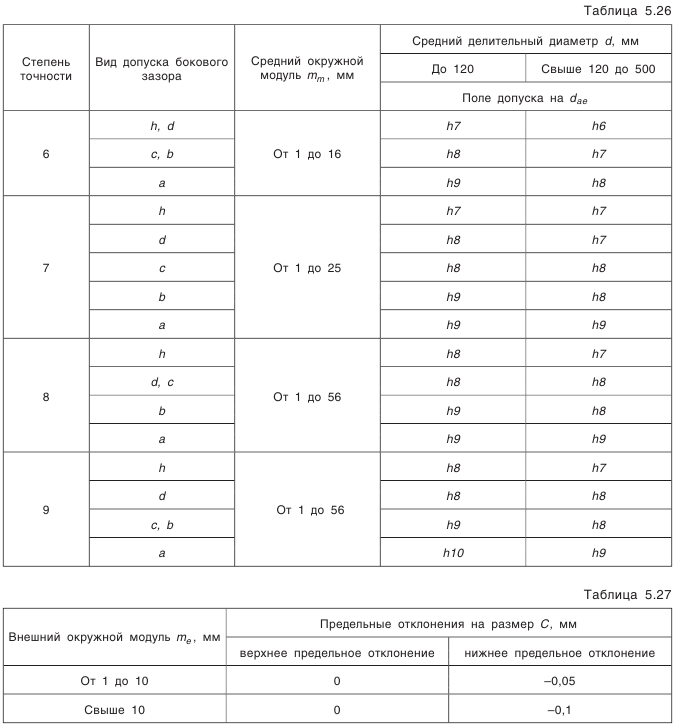
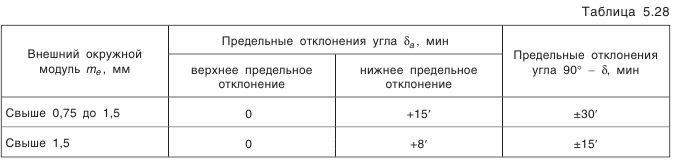
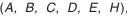 , и пять видов допусков на боковой зазор (рис. 5.21).
, и пять видов допусков на боковой зазор (рис. 5.21).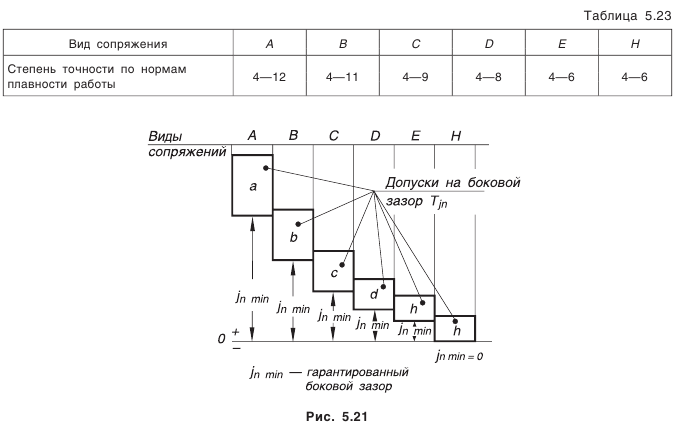
 :
:
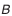 :
:
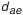 ; внешний диаметр вершин зубьев после притупления кромки
; внешний диаметр вершин зубьев после притупления кромки 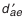 ; расстояние от базовой плоскости до плоскости внешней окружности вершин зубьев
; расстояние от базовой плоскости до плоскости внешней окружности вершин зубьев 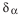 ; угол внешнего дополнительного конуса
; угол внешнего дополнительного конуса 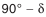 ; ширина зубчатого венца
; ширина зубчатого венца 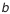 ; базовое расстояние А(Ц) — размер, входящий в размерную цепь; положение измерительного сечения; размеры фасок или радиусы кривизны линий притупления на кромках зубьев. Допускается указывать размеры фасок или радиусы кривизны линий притупления в технических требованиях чертежа.
; базовое расстояние А(Ц) — размер, входящий в размерную цепь; положение измерительного сечения; размеры фасок или радиусы кривизны линий притупления на кромках зубьев. Допускается указывать размеры фасок или радиусы кривизны линий притупления в технических требованиях чертежа.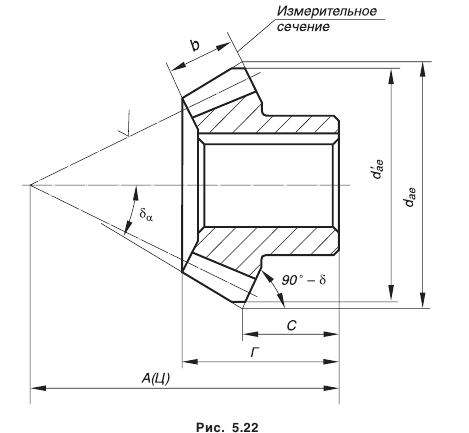
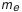 .
. .
.

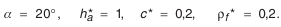
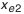 .
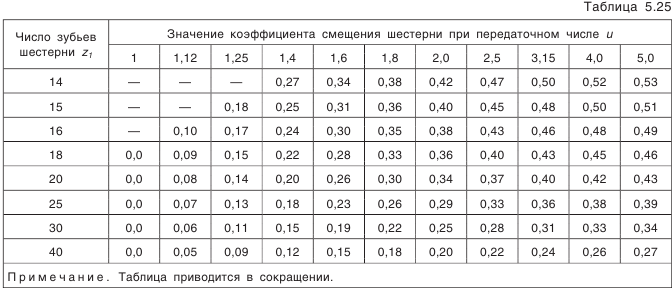
.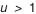 шестерню рекомендуется выполнять с положительным смещением по табл. 5.25, а колесо с равным ему по величине отрицательным смещением. Принимается
шестерню рекомендуется выполнять с положительным смещением по табл. 5.25, а колесо с равным ему по величине отрицательным смещением. Принимается 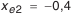 .
.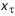 .
.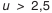 зубчатые колеса рекомендуется выполнять с различной толщиной зуба, увеличенной у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса. Коэффициент изменения толщины зуба принимается
зубчатые колеса рекомендуется выполнять с различной толщиной зуба, увеличенной у исходного контура шестерни и соответственно уменьшенной у исходного контура колеса. Коэффициент изменения толщины зуба принимается 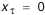 , так как
, так как  .
.
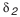 .
.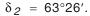
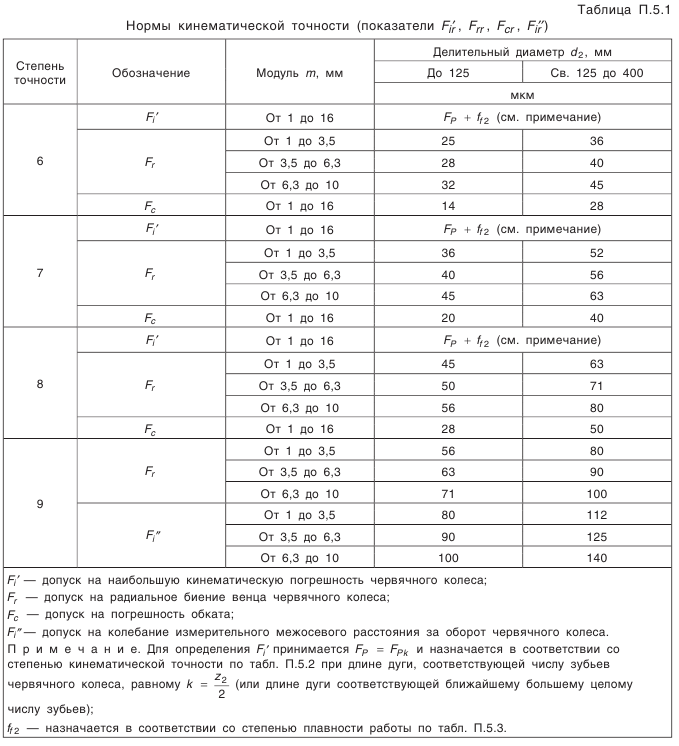
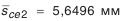 (см. табл. 5.21) и предельные отклонения на нее, которые определяют боковой зазор (расчет предельных отклонений см. ниже);
(см. табл. 5.21) и предельные отклонения на нее, которые определяют боковой зазор (расчет предельных отклонений см. ниже);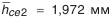 (см. табл. 5.21).
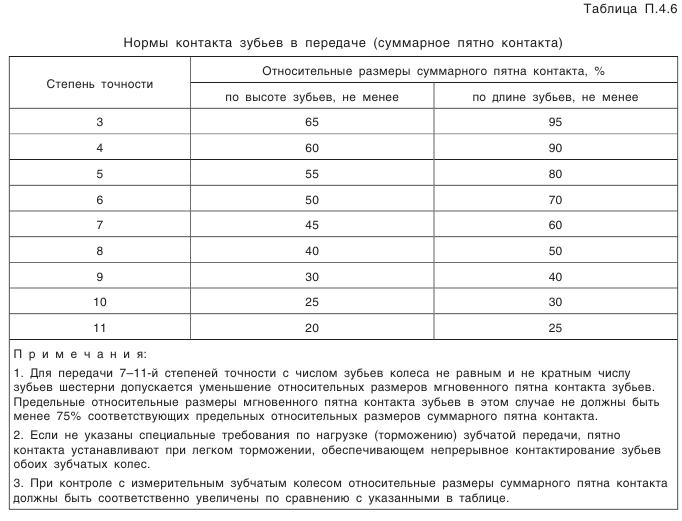
(см. табл. 5.21).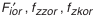 и относительные размеры суммарного пятна контакта.
и относительные размеры суммарного пятна контакта. . Выбранное измерительное сечение (см. рис. 5.23) находится на торце зубчатого колеса, поэтому выбранные значения наименьшего отклонения и допуска следует увеличить в
. Выбранное измерительное сечение (см. рис. 5.23) находится на торце зубчатого колеса, поэтому выбранные значения наименьшего отклонения и допуска следует увеличить в 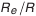 раз, где
раз, где 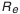 — внешнее конусное расстояние.
— внешнее конусное расстояние.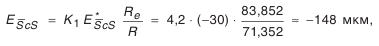
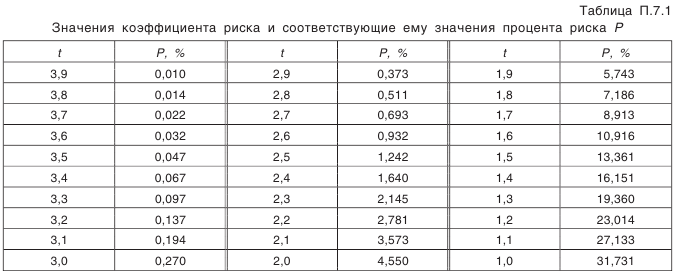
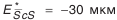 — наименьшее отклонение средней постоянной хорды зуба (см. табл. П.6.7, приложение 6);
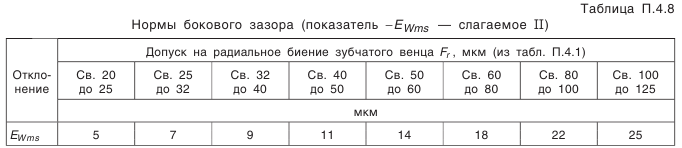
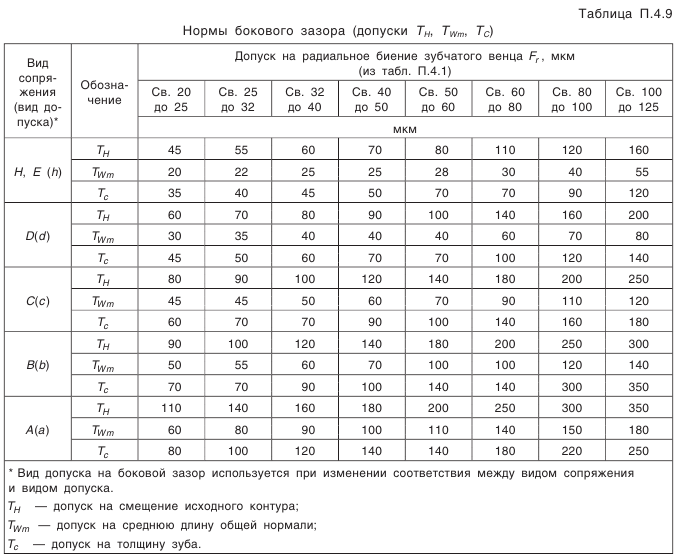
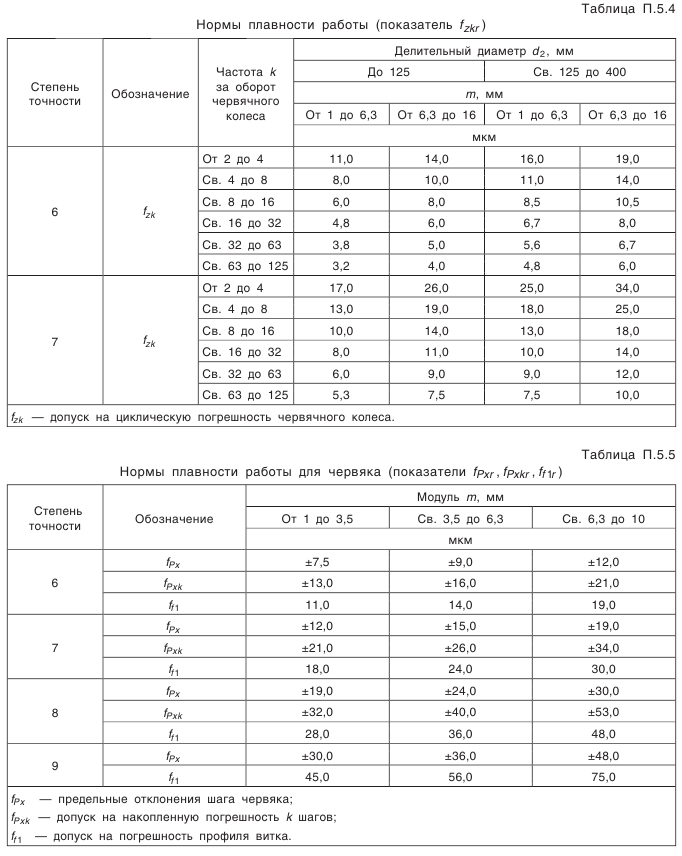
— наименьшее отклонение средней постоянной хорды зуба (см. табл. П.6.7, приложение 6);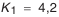 — коэффициент, определяемый по табл. П.6.8 (приложение 6). Допуск на среднюю постоянную хорду:
— коэффициент, определяемый по табл. П.6.8 (приложение 6). Допуск на среднюю постоянную хорду: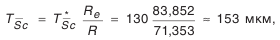
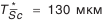 (см. табл. П.6.9).
(см. табл. П.6.9).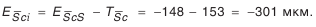
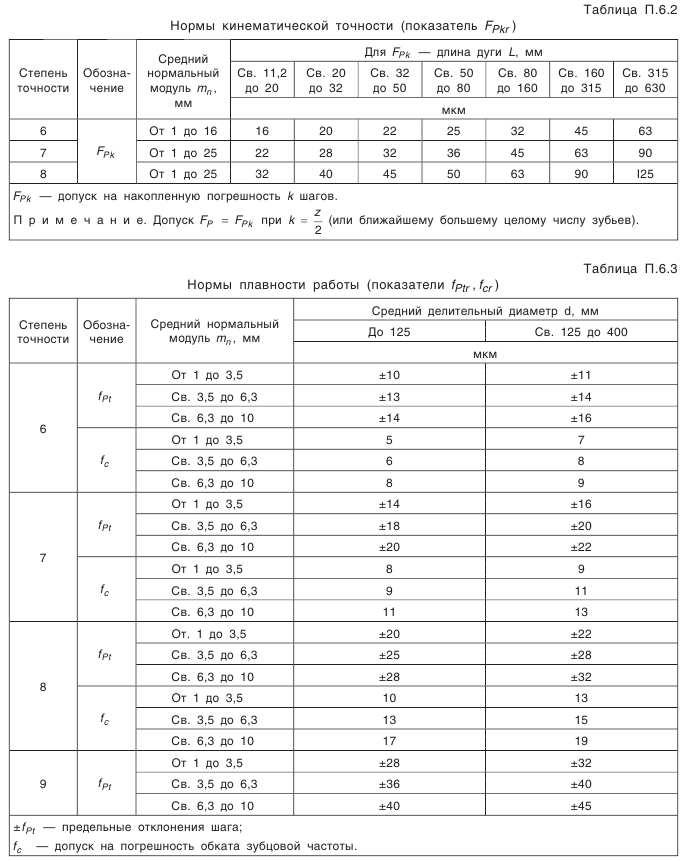
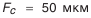 (см. табл. П.6.1, приложение 6);
(см. табл. П.6.1, приложение 6);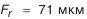 (см. табл. П.6.1, приложение 6).
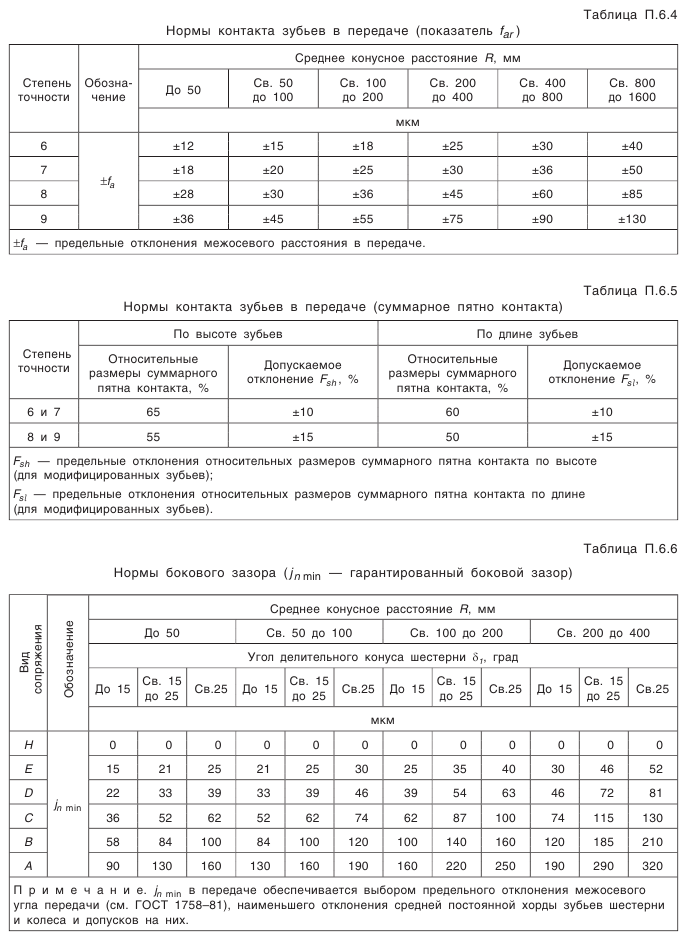
(см. табл. П.6.1, приложение 6).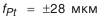 (см. табл. П.6.3);
(см. табл. П.6.3);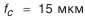 (см. табл. П.6.3, приложение 6).
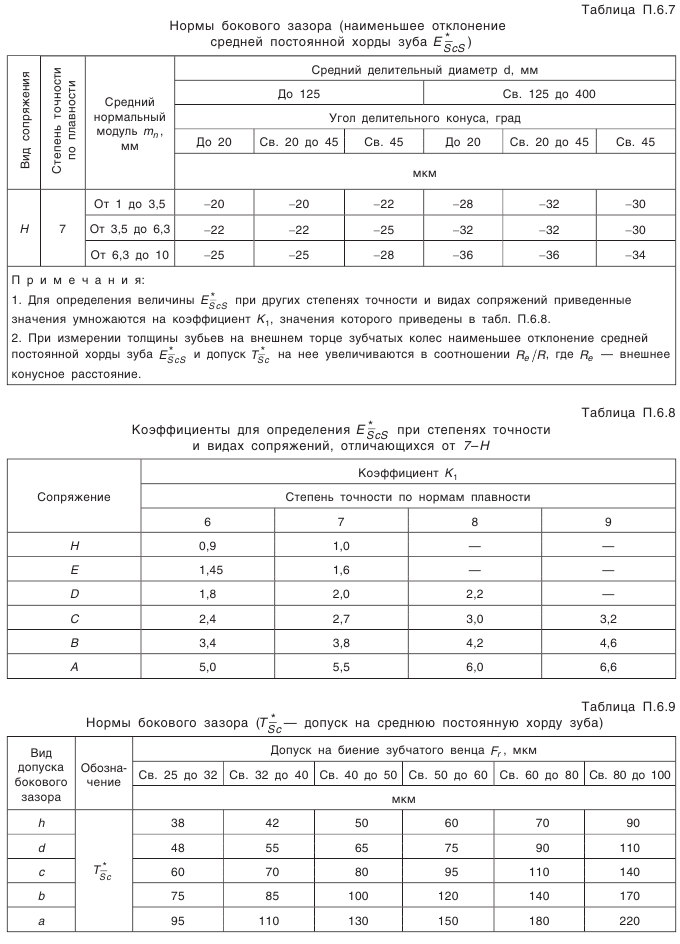
(см. табл. П.6.3, приложение 6).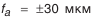 (табл. П.6.4);
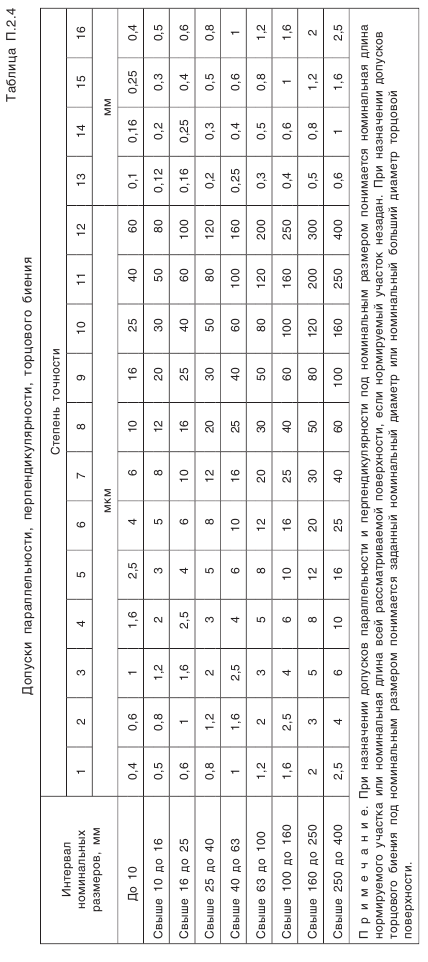
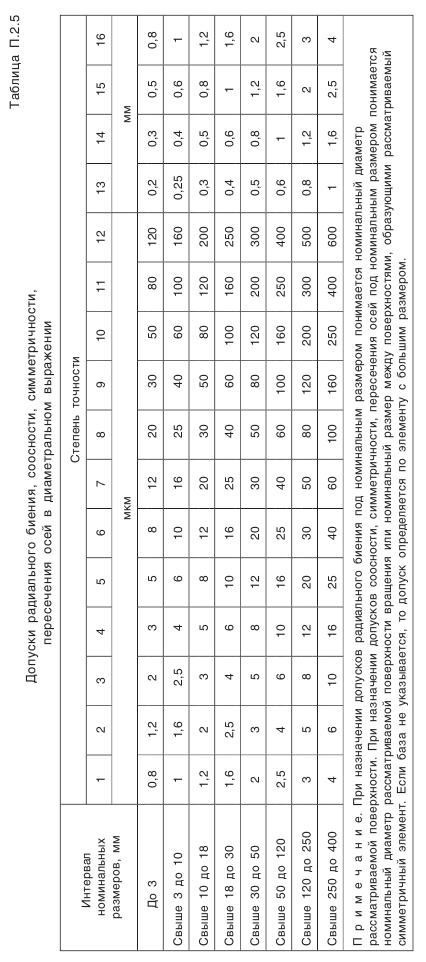
(табл. П.6.4);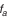 ограничивает допустимую величину отклонения от пересечения осей. Предельные отклонения задаются относительно рабочей оси колеса и, следовательно, включают как погрешность изготовления колеса, так и погрешности, возникающие при монтаже его в механизме, например торцовое биение базового буртика вала (рис. 5.24).
ограничивает допустимую величину отклонения от пересечения осей. Предельные отклонения задаются относительно рабочей оси колеса и, следовательно, включают как погрешность изготовления колеса, так и погрешности, возникающие при монтаже его в механизме, например торцовое биение базового буртика вала (рис. 5.24).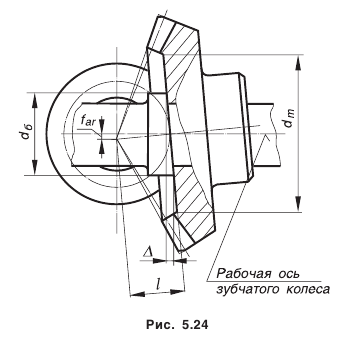
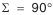 (см. табл. 5.20);
(см. табл. 5.20);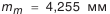 (см. табл. 5.21);
(см. табл. 5.21);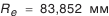 (см. табл. 5.21);
(см. табл. 5.21);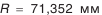 (см. табл. 5.21);
(см. табл. 5.21);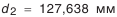 (см. табл. 5.21);
(см. табл. 5.21);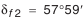 (см. табл. 5.21);
(см. табл. 5.21);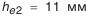 (см. табл. 5.21);
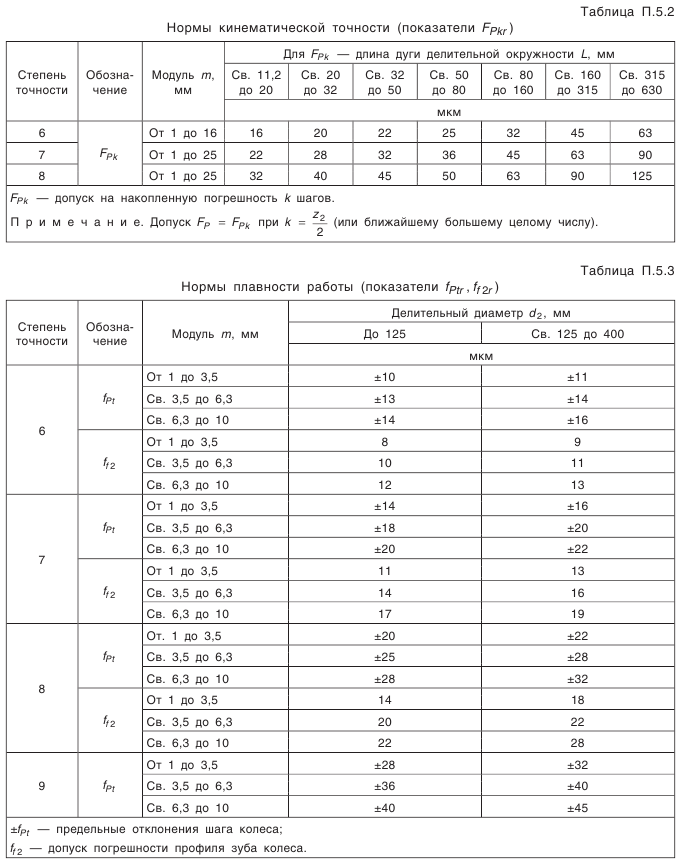
(см. табл. 5.21); и допуск на него. Расчет диаметра приведен в табл. 5.21:
и допуск на него. Расчет диаметра приведен в табл. 5.21: 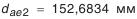 .
.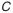 (см. рис. 5.22) и допуск на него.
(см. рис. 5.22) и допуск на него.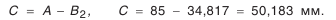
 и угол внешнего делительного дополнительного конуса
и угол внешнего делительного дополнительного конуса 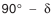 .
.
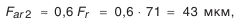
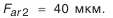
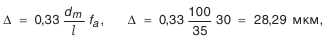
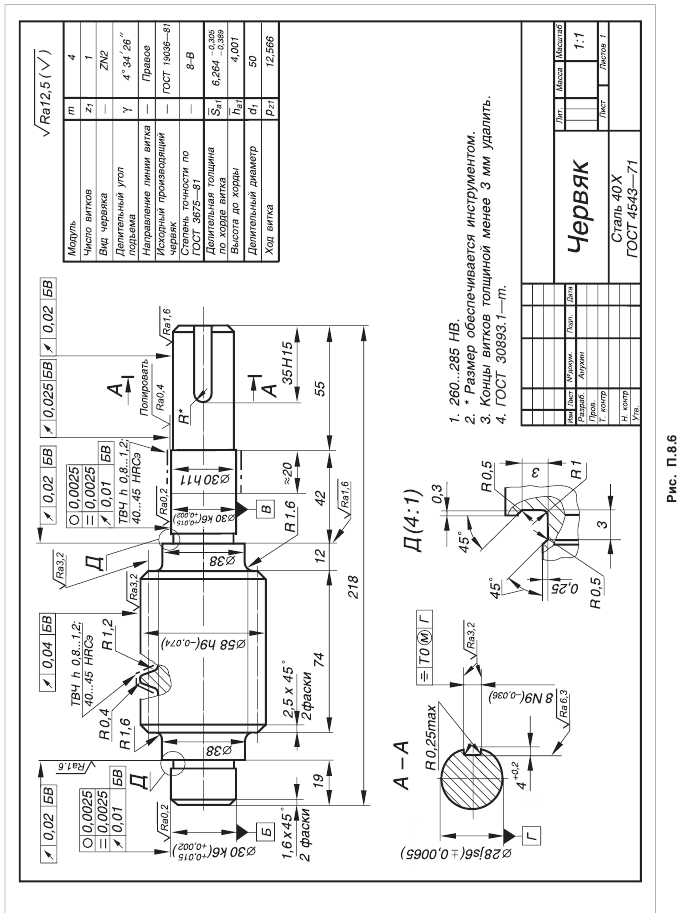
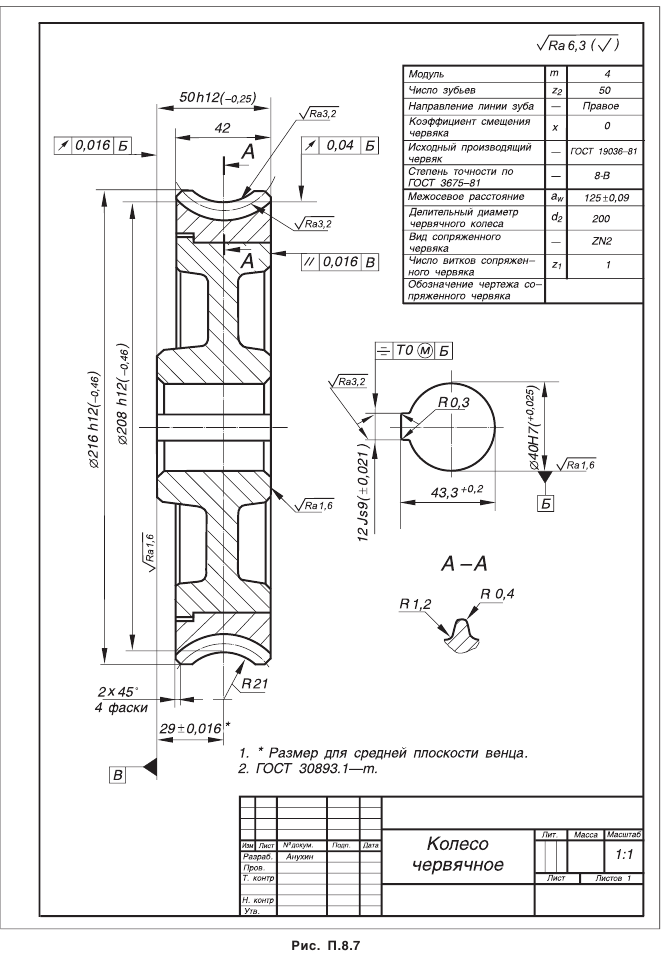
 — диаметр базового торца колеса, рассчитывается по данным чертежа (см. рис. П.8.8, приложение 8);
— диаметр базового торца колеса, рассчитывается по данным чертежа (см. рис. П.8.8, приложение 8);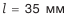 — расстояние от вершины конуса колеса до его базового торца (см. рис. 5.23 и 5.24);
— расстояние от вершины конуса колеса до его базового торца (см. рис. 5.23 и 5.24); 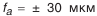 — предельные отклонения межосевого расстояния в передаче (см. табл. П.6.4, приложение 6);
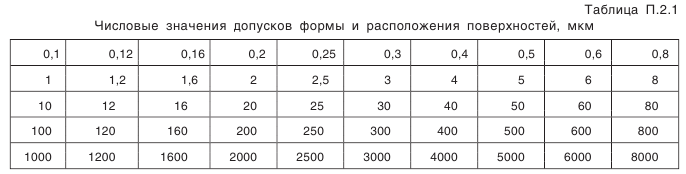
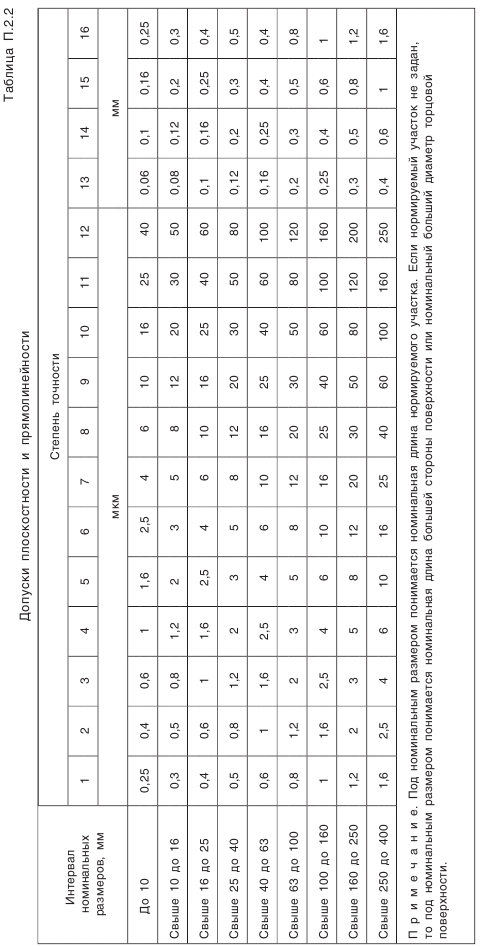
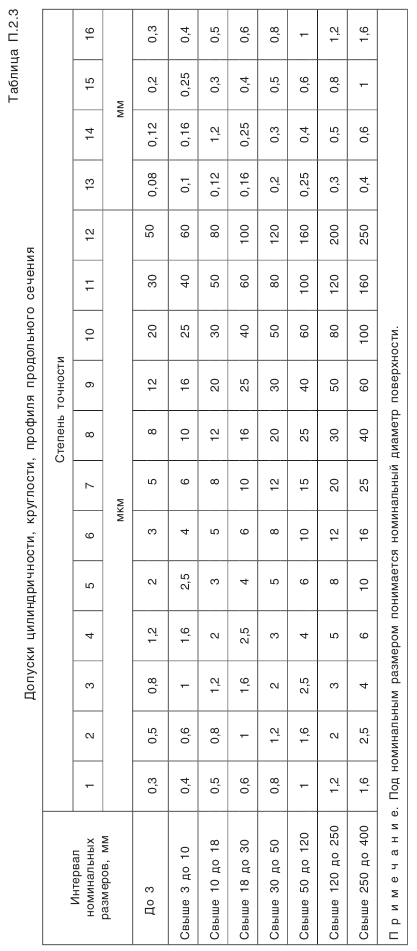
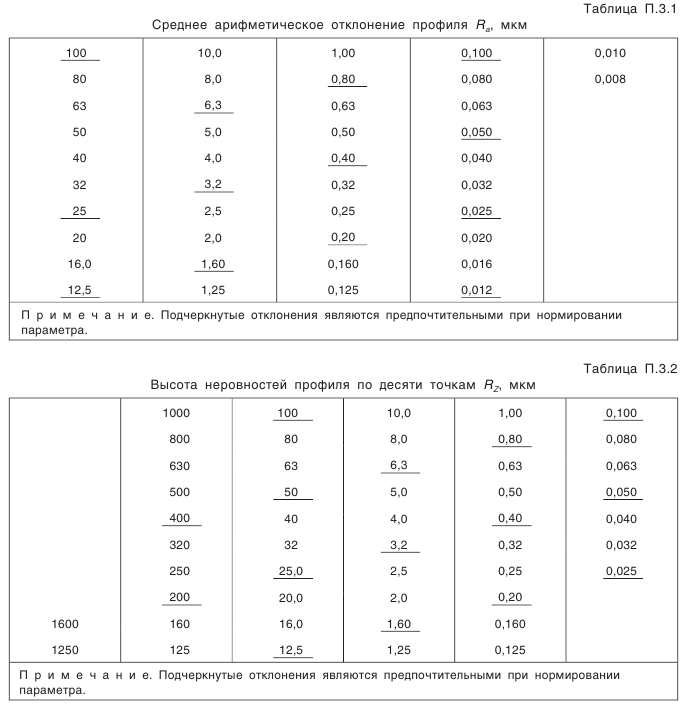
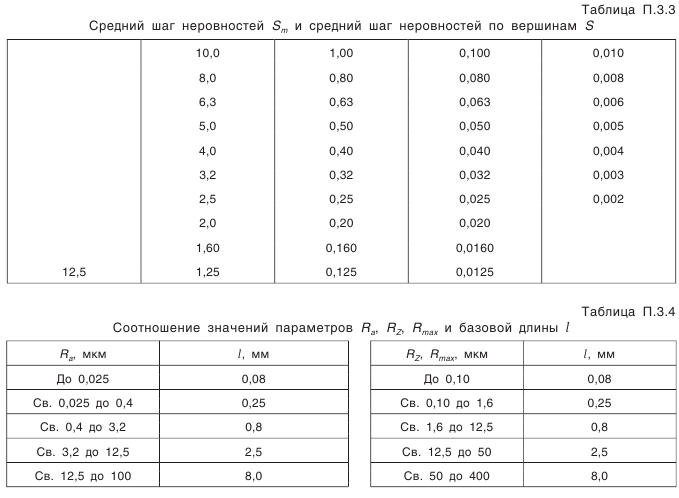
— предельные отклонения межосевого расстояния в передаче (см. табл. П.6.4, приложение 6);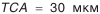 (см. табл. П.2.4, приложение 2). Позиция 15. Шероховатость профилей зубьев колеса.
(см. табл. П.2.4, приложение 2). Позиция 15. Шероховатость профилей зубьев колеса.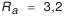 выбирается по наивысшей степени точности, в предложенном примере — по 8-й степени точности (см. табл. 5.6).
выбирается по наивысшей степени точности, в предложенном примере — по 8-й степени точности (см. табл. 5.6).