Что такое весовой граф

Теория Графов. Часть 1 Введение и классификация графов

«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Схема Московского метро

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Нулевой граф

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Множество E задается парой неупорядоченных вершин множества V.

Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =

Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Формула суммы степеней для G = V,E выглядит так:

То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Классификации графов

Первым признаком классификации является отсутствие или наличие ориентации у ребер.

Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Неориентированный граф

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Ориентированный граф

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Смешанный граф

Вторым признаком является отсутствие или наличие кратных ребер.

Мультиграф

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.

Заключение

В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.

Источник

Содержание урока

Взвешенный граф

Взвешенный граф

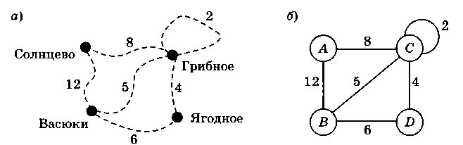
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Следующая страница Оптимальный путь в графе

Cкачать материалы урока

Источник

11. Взвешенный граф. Кратчайшие пути во взвешенном графе и алгоритм Форда постро-ения кратчайших маршрутов

На взвешенном графе 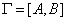с весовой функцией можно ввести понятие Рассто-яния между вершинами. Делается это так.

Будем считать далее, если не будет специальных оговорок, что все рассматриваемые гра-фы связны. Вес любого пути будем называть Длиной этого пути. Ясно, что между двумя верши-нами существует такой путь, который имеет минимальную возможную длину. Эта длина и на-зывается Расстоянием между двумя вершинами. Путь, который эту длину реализует, естествен-но, называется Кратчайшим.

Существует классический Алгоритм Форда поиска кратчайших путей в графе. Основан он на следующем простом факте: Если имеется кратчайший путь между какими-либо двумя вершинами, то его часть между любыми двумя вершинами на нем же самом также является кратчайшим путем.

Алгоритм Форда позволяет найти кратчайшие пути из какой-либо одной вершины графа во все остальные. Эту исходную вершину можно выбрать произвольно, но, сделав выбор, далее уже исходить из того, что будут описаны кратчайшие пути именно из этой вершины во все остальные.

Опишем алгоритм по шагам.

Шаг 0. Занумеруем все вершины из 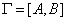, так что и при этом номер «1» имеет именно та вершина, из которой будут найдены кратчайшие пути во все остальные вершины. Построим, далее матрицу , положив

Шаг 1. Около первой строки матрицы 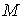, слева от матрицы, поставим числовую помет-ку «0» и такую же пометку проставим над первым столбцом матрицы. Затем просмотрим поме-ченную строку слева направо и всякий раз, встречая клетку с числом, прибавим это число к по-метке строки и сумму проставим над столбцом, в котором эта клетка находится.

Затем отразим пометки столбцов относительно главной диагонали. Возникнут помечен-ные строки. С каждой из помеченных строк проделаем то же самое: просмотрим помеченную строку слева направо и всякий раз, встречая клетку с числом, прибавим это число к пометке строки и сумму поставим в качестве пометки над столбком, в котором эта клетка стоит. При этом будем соблюдать принцип Ã: «имеющуюся пометку не менять».

Затем пометки столбцов отразим относительно главно диагонали и с помеченными стро-ками вновь проделаем то же самое. И так далее, пока не окажутся помеченными все строки и все столбцы.

Шаг 2. Просмотрим строки таблицы в порядке возрастания их номеров. В каждой строке просматриваются клетки слева направо и всякий раз, когда встречается число, оно складывает-ся с пометкой строки и сумма сравнивается с пометкой столбца, в котором найденное число расположено. Если сумма оказалась меньше, чем пометка столбца, то эта пометка столбца заме-няется на упомянутую сумму. Если же сумма оказалась больше или равной пометке, то ничего не меняется.

После такого просмотра всех строк новые пометки столбцов отражаются относительно главной диагонали и вся процедура повторяется. И так до тех пор пока не прекратятся какие бы то ни было изменения в пометках.

Шаг 3. Теперь по пометкам можно построить кратчайшие пути из первой вершины во все остальные. Фиксируем произвольную вершину и опишем кратчайший путь из первой вершины в вершину . Во-первых, длина этого кратчайшего пути равна помет-

Ке , стоящей над столбцом номер . Во-вторых, Предпоследняя Вершина в кратчайшем пути из первой вершины в вершину находится так: в столбце номер отыскиваем число, сумма которого с пометкой строки, в которой оно расположено, равна . Пусть номер строки, в ко-торой найденное число оказалось, равен . Тогда предпоследней вершиной в кратчайшем пути из 1 в будет вершина . (Разумеется, всё только что сказанное нуждается в доказательсвах,

Которые не приводятся.) Вершину, которая предшествует вершине , надо отыскивать как предпоследнюю в кратчайшем пути из 1 в и так далее.

Приведем пример. Пусть исходный взвешенный граф дает следующую матрицу :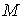

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Графы

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§17. Графы.

Что такое граф?

Ключевые слова:

Давайте подумаем, как можно наглядно представить такую информацию:

От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

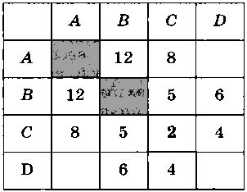
Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

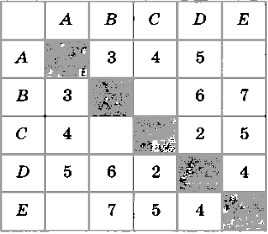
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»

Источник