Что такое весовая матрица в информатике определение

Содержание урока

Взвешенный граф

Взвешенный граф

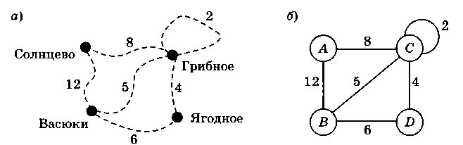
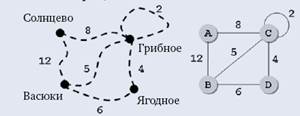
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Следующая страница Оптимальный путь в графе

Cкачать материалы урока

Источник

Весовая матрица графа это

В случае ориентированного графа с n вершинами и m дугами элемент матрицы инцидентности равен:

Строки матрицы также соответствуют вершинам, а столбцы – дугам.

Матрица инцидентности однозначно определяет структуру графа (см. рис. 1.1. а–в, д-ж). В каждом столбце матрицы B ровно две единицы. Равных столбцов нет.

Недостаток данного представления состоит в том, что требуется n m единиц памяти, большинство из которых будет занято нулями. Не всегда удобен доступ к информации. Например, для ответа на вопросы “есть ли в графе дуга (x, y)?” или “к каким вершинам ведут ребра из вершины x?” может потребоваться перебор всех столбцов матрицы.

Итак, граф — это (непустое) множество вершин и множество соединяющих их ребер. Эта структура естественно появляется тогда, когда в задаче есть несколько однотипных объектов и каждый из них может быть связан с произвольным количеством других объектов. В качестве объектов могут быть железнодорожные станции, маршрутизаторы локальных и глобальных сетей и т.п. В первом случае ребра графа — это дороги между станциями, во втором — каналы связи (кабельные, оптоволоконные, спутниковые и т.д.).

Для человека наиболее естественно использовать изображения графов (рисунки, схемы) для объяснения связей между элементами какой-то системы. Поскольку информатика занимается автоматической обработкой данных с помощью компьютеров, сразу возникает вопрос: “Как представить информацию о графе в памяти компьютера?” Хранить ее в виде рисунка (растрового или векторного) неэффективно, потому что рисунок предназначен для восприятия человеком, а не компьютером.

Компьютеру удобнее всего хранить информацию в виде таблиц (массив тоже можно считать простейшей таблицей). Для описания графа часто используют квадратную таблицу, которая описывает все возможные связи между узлами (без учета дублирования). Если, например, на пересечении строки Aи столбца Bзаписано число 1, это означает, что есть ребро, соединяющее вершины Aи B; число 0 в этой ячейке означает, что такого ребра нет. Такую таблицу называют матрицей смежности. На рисунке показанаи схема дорог, соответствующий ей

граф и его матрица смежности:

Единица на главной диагонали (выделенной серым цветом) показывает, что в графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Обратите внимание, что матрица смежности симметрична относительно главной диагонали, то есть если существует ребро из вершины Aв вершину B, то существует и ребро из Bв A. Такой граф называют неориентированным — ребра не имеют направления и каждое из них учтено в матрице смежности дважды.

Во многих практических задачах (например, при определении кратчайшего пути из одной вершины в другую) важную роль играет не только наличие связей между вершинами, но и “длины” этих связей, которые в теории графов называют “весами” (от слова “вес”). Весом может быть, например, длина дороги или стоимость авиаперелета. В этом случае вместо матрицы смежности используют весовую матрицу, в клетках которой записывают веса ребер, а если ребра нет, то клетку оставляют пустой. На рисунке показана схема, на которой указаны длины дорог, соответствующий ей граф и его весовая матрица:

Заметим, что весовая матрица никак не определяет взаимное расположение вершин. Например, рассмотренный выше граф можно нарисовать совсем иначе, например, так:

Однако с точки зрения теории графов это будет тот же самый граф, поскольку весовая матрица не изменилась. По аналогии можно вспомнить, что в математике записи 0,5, 1/2, 3/6 и 5/10 обозначают одно и то же число.

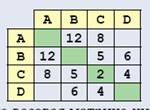
Что можно выяснить с помощью весовой матрицы? Во-первых, определить, есть ли ребро между двумя заданными вершинами, и если есть, какова его длина (вес). Для этого достаточно посмотреть в соответствующую ячейку. Например, значение, выделенное кружком на рисунке, показывает, что между вершинами Bи Cесть ребро с весом 5:

Предполагая, что веса ребер обозначают расстояния между вершинами, можно определить длину пути, проходящего через заданные вершины, — сумму длин ребер, составляющих этот путь. В данном случае длина замкнутого пути ABCDAскладывается из длин ребер AB, BC, CDи DA, которые определяются по таблице. Получаем: 3 + 5 + 6 + 4 = 18.

Наконец, полезно научиться рисовать граф по заданной весовой матрице. Нужно только помнить, что это можно сделать разными способами.

Для последней приведенной матрицы рисунок может быть, например, таким:

Вопросы и задачи:

1) Как по весовой матрице графа определить количество ребер (количество петель)?

2) Как можно обозначить отсутствие связи между вершинами при хранении весовой матрицы в памяти реального компьютера (рассмотрите разные варианты)?

3) Для каждой приведенной ниже весовой матрицы:

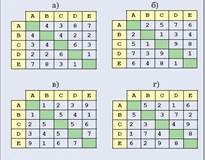
· определите вес ребра между вершинами Bи D(если оно есть);

· предполагая, что веса ребер обозначают расстояния между вершинами, определите длину пути ABDCEA;

· укажите, какой из трех путей — ABDC, ADECили AEBC— самый короткий, а какой самый длинный:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9465 – | 7448 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Матрица смежности — один из способов представления графа в виде матрицы.

Содержание

Определение [ править | править код ]

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i-й вершины.

Матрица смежности простого графа (не содержащего петель и кратных рёбер) является бинарной матрицей и содержит нули на главной диагонали.

Матрица смежности двудольного графа [ править | править код ]

Матрица смежности A двудольного графа, доли которого имеют r и s вершин, может быть записана в следующем виде

>,>

Примеры [ править | править код ]

Граф	Матрица смежности
	( 1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 0 0 0 1 0 0 ) >

Свойства [ править | править код ]

Матрица смежности неориентированного графа симметрична, а значит обладает действительными собственными значениями и ортогональным базисом из собственных векторов. Набор её собственных значений называется спектром графа, и является основным предметом изучения спектральной теории графов.

Два графа G₁ и G₂ с матрицами смежности A₁ и A₂ являются изоморфными тогда и только тогда, когда существует перестановочная матрица P, такая что

Из этого следует, что матрицы A₁ и A₂ подобны, а значит имеют равные наборы собственных значений, определители и характеристические многочлены. Однако обратное утверждение не всегда верно — два графа с подобными матрицами смежности могут быть неизоморфны (это бывает в случае, если матрица P не является перестановочной, например, матрицы ( 0 1 0 0 ) > и ( 0 2 0 0 ) > являются подобными, но соответствующие им графы не изоморфны).

Степени матрицы [ править | править код ]

Если A — матрица смежности графа G, то матрица A m обладает следующим свойством: элемент в i-й строке, j-м столбце равен числу путей из i-й вершины в j-ю, состоящих из ровно m ребер.

Структура данных [ править | править код ]

Матрица смежности и списки смежности являются основными структурами данных, которые используются для представления графов в компьютерных программах.

Использование матрицы смежности предпочтительно только в случае неразреженных графов, с большим числом рёбер, так как она требует хранения по одному биту данных для каждого элемента. Если граф разрежён, то большая часть памяти напрасно будет тратиться на хранение нулей, зато в случае неразреженных графов матрица смежности достаточно компактно представляет граф в памяти, используя примерно n 2 > бит памяти, что может быть на порядок лучше списков смежности.

В алгоритмах, работающих со взвешенными графами (например, в алгоритме Флойда-Уоршелла), элементы матрицы смежности вместо чисел 0 и 1, указывающих на присутствие или отсутствие ребра, часто содержат веса самих рёбер. При этом на место отсутствующих рёбер ставят некоторое специальное граничное значение (англ. sentinel ), зависящее от решаемой задачи, обычно 0 или ∞ .

Источник

Информатика. 11 класс

Конспект урока

Информатика, 11 класс. Урок № 7.

Тема — Моделирование на графах

Цели и задачи урока:

На уроке вы узнаете:

Давайте рассмотрим, пожалуй, самую известную головоломку, придуманную аж в XVIII веке, и захватившую умы человечества на многие годы. Называется она задача о семи Кёнигсбергских мостах. В Кёнигсберге начиная с XIV было построено 7 мостов: Медовый мост, Лавочный мост, Зелёный мост, Рабочий мост, Кузнечный мост, Деревянный мост и Высокий мост, соединяющий остров и полуострова в единый город. Тогда и возникла головоломка: «Как пройти по всем мостам, не проходя ни по одному дважды?»

Десятилетиям жители города пытались решить эту задачу как практически (гуляя по городу), так и теоретически.

И только Леонард Эйлер, введя новое понятие — ГРАФ, смог решить ее раз и навсегда.

Граф — абстрактный математический объект, представляющий собой множество вершин графа (обозначены красным цветом) и набор рёбер (обозначены синим), то есть соединений между парами вершин. При этом каждое ребро представляет собой отношение двух вершин.

— Неориентированные и ориентированные (когда движение по ребру возможно только в одну сторону).

— Взвешенными (когда у вершины или у ребра есть вес, отличающий его от другого) и невзвешенный.

— И другие более сложные графы (мультиграф, псевдограф, изоморфный граф и другие).

Эйлер установил, что:

1. Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно или не может существовать граф, который имел бы нечётное число нечётных вершин.

2. Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.

3. Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

ВЫВОД: пройти только один раз по каждому мосту невозможно.

Графы находят широкое применение во многих сферах нашей жизни. Например, с их помощью можно планировать оптимальные транспортные маршруты, упростить решение математических задач, визуализировать решения компьютерных программ, визуализировать различную информацию (схема метро, карта звездного неба и т. д.).

Очень часто для решения задач требуется найти кратчайший путь между двумя вершинами.

Кратчайшим путем мы будем называть путь, если: эти вершины соединены минимальным числом ребер (в случае, если граф невзвешенный); сумма ребер, соединяющих эти вершины, минимальна (для взвешенного графа).

Существует огромное количество алгоритмов, находящих кратчайший путь и один из них — это алгоритм Дейсктры.

Алгоритм заключается в том, что надо пошагово перебрать все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.

Для примера возьмем следующий взвешенный ориентированный граф и попытаемся найти кратчайший путь от вершины A до F. Пошагово переберём все вершины графа, вычеркивая их, которые будут являются известным минимальным расстоянием от вершины «начала» до конкретной вершины.

Первым шагом: присвоим вершине А метку равную 0, потому как эта вершина — начало. Остальным вершинам присвоим метки равные бесконечности.

Вторым шагом: выберем не вычеркнутую вершину, вес которой является минимальным («источник»). Сейчас это вершина А. Вычисляем сумму веса вершины источника и веса ребра

Если она окажется меньше веса вершины приемника, то изменим вес этой вершины.

Третьим шагом: вычеркнем вершину-«источник».

Повторим шаги 1, 2, 3 до тех пор, пока не будут вычеркнуты все вершины.

Еще один способом нахождения кратчайшего пути может служить «метод динамического программирования».

Пусть дан некоторый лабиринт, соединяющий комнаты в виде графа. При этом заходя в каждую комнату, нужно заплатить пошлину. Необходимо пройти по нему от точки А до точки В, потратив наименьшее количество денег.

Составим таблицу, в которой каждая ячейка будет соответствовать определенной ячейке. Числа в ячейках будут равны минимальному числу пошлины, которое можно получить, пройдя от начала (A) до соответствующей клетки.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Графы

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§17. Графы.

Что такое граф?

Ключевые слова:

Давайте подумаем, как можно наглядно представить такую информацию:

От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

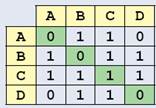
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

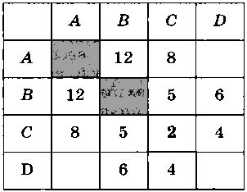
Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

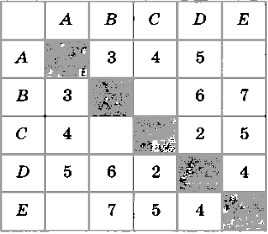
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

Подготовьте сообщение

а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»

Источник