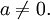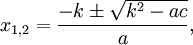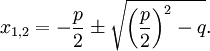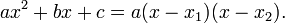Что такое вещественный корень

Алгоритм расчёта вещественных корней полиномов

Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

А теперь по порядку.

Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.

Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.

Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.

В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.

Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.

Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.

Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.

Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.

Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.

Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+. +k[1]*x+k[0] по схеме Горнера.

На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.

Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.

Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.

Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.

Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt =vg)break;.

В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.

Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.

Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.

Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.

Литература

1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты

Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1

Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:

Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.

Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.

Источник

Корень квадратного уравнения

Квадратное уравнение — уравнение вида ax 2 + bx + c = 0, где

Содержание

Уравнение с вещественными коэффициентами

Квадратное уравнение с вещественными коэффициентами 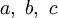может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b 2 − 4ac:

Другие записи решений

Вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение

Приведённое квадратное уравнение

Квадратное уравнение вида x 2 + px + q = 0, в котором старший коэффициент a равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до

Мнемонические правила

Уравнение с комплексными коэффициентами

В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше ее вариантам, но различимыми является только два случая: нулевого дискриминанта (один корень) и ненулевого (два корня).

Теорема Виета

В общем случае (для неприведённого квадратного уравнения ax 2 + bx + c = 0 ):

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

См. также

Ссылки

Полезное

Смотреть что такое «Корень квадратного уравнения» в других словарях:

Корень (в математике) — Корень в математике, 1) К. степени n из числа а ≈ число х (обозначаемое ), n я степень которого равна а (то есть xn = а). Действие нахождения К. называют извлечением корня. При а ¹ 0 существует n различных значений К. (вообще говоря,… … Большая советская энциклопедия

Разложение Квадратного трехчлена — Квадратное уравнение уравнение вида ax2 + bx + c = 0, где Содержание 1 Уравнение с вещественными коэффициентами … Википедия

Разложение квадратного трехчлена — Квадратное уравнение уравнение вида ax2 + bx + c = 0, где Содержание 1 Уравнение с вещественными коэффициентами … Википедия

Квадратные уравнения — Квадратное уравнение уравнение вида ax2 + bx + c = 0, где Содержание 1 Уравнение с вещественными коэффициентами … Википедия

Кубический корень — График функции y = Кубический (кубичный) корень из a решение уравнения (обычно п … Википедия

Метод Мюллера — итерационный численный метод для вычисления корня заданной функции f(x) = 0. Был представлен Давидом Мюллером в 1956 году. Метод Мюллера основан на методе секущих, который строит на каждом шаге итерации прямые, проходящие через две точки на… … Википедия

ИСТИННЫЙ КОЭФФИЦИЕНТ — еcтественного прироста нас., собственный коэффициент естественного прироста, коэффициент прогрессивности режима воспроиз ва, коэффициент Лотки, коэфф. естеств. прироста стабильного населения, соответствующего данному режиму воспроиз ва нас. И. к … Демографический энциклопедический словарь

Источник

Большая Энциклопедия Нефти и Газа

Вещественный корень

Сколько вещественных корней имеет уравнение х sinx О. [5]

Если вещественный корень лежит на мнимой оси, то, следовательно, он равен нулю. [6]

Если вещественный корень будет расположен близко к вещественному нулю, то в разложении на простые дроби изображения по Лапласу выходной переменной коэффициент при члене, соответствующем данному корню, будет достаточно малым и влияние этого корня на реакцию системы окажется незначительным. Однако проектировщик должен постоянно помнить, что реакция скорректированной системы определяется не только корнями ее характеристического уравнения, но и нулями передаточной функции. Поэтому всегда целесообразно во избежание ошибок при синтезе проверять показатели качества скорректированной системы путем компьютерного моделирования. [7]

Преобразовать полученные вещественные корни с помощью стандартной функции Fioattostr в текстовые величины, годные для вывода в текстовых окнах. [9]

Его простые вещественные корни определяют замкнутые фазовые кривые невозмушенной системы, от которых под действием возмущения родятся предельные циклы. [10]

Наличие вещественных корней в этом уравнении является указанием на возможность существования волны Стоунли для данной пары материалов. [11]

Если вещественных корней нет, то заданного, значения г / гаах не достигает ни одна капля. Если есть два различных вещественных корня PI и ф2, то заданная высота является максимальной для двух капель. Это отчетливо видно из рис. 8.4 задачи 8 про мокрое колесо. Наибольшей высоты из всех капель, как видно из того же рисунка, достигает только одна капля. [12]

А лишь вещественные корни ; обозначим их через Я. [13]

Если один вещественный корень или пара комплексных сопряженных корней расположены на мнимой оси комплексной плоскости, то система находится на границе устойчивости. Линейные системы, характеристические уравнения которых имеют пару мнимых корней, могут совершать незатухающие свободные колебания. [14]

АО есть вещественный корень этого уравнения. [15]

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Локализация корней полинома

Пример [Уилкинсон]. Вычислить корни полинома

Правило знаков Декарта

Теорема [Декарт]. Число положительных корней полинома

Доказательство ☞ ЗДЕСЬ.

С помощью преобразования корней полинома (см. пункт 1 ☞ ЗДЕСЬ ) можно доказать следствие:

Число отрицательных корней полинома

Если из каких-то соображений известно, что все корни полинома вещественны, то число положительных из них определяется по правилу знаков Декарта однозначно:

Система полиномов Штурма

Обобщенная система полиномов Штурма

Ганкелевы матрицы в теории локализации корней

Ответ. Три вещественных корня.

Имеет место соотношение

Пример. Определить число вещественных корней полинома

Формула Маркова

Устойчивость

Локализация собственных чисел матрицы

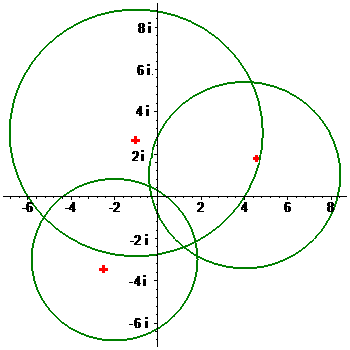
Теорема Гершгорина

Пример. Построить круги Гершгорина для матрицы

Симметричные матрицы

Доказательство ☞ ЗДЕСЬ.

Совместность

Мы рассмотрим здесь только общий случай, т.е. будем считать выполненными следующие предположения.

Теорема. При выполнении условий предположений 1 и 2 система неравенств будет совместна тогда и только тогда, когда выполнено хотя бы одно из следующих условий:

Условие пункта b) теоремы можно проверить по теореме Эрмита-Сильвестра с использованием формулы Маркова.

Пример. Исследовать на совместность систему

Эту рекомендацию можно обобщить.

Статья не закончена!

Определение структуры множества решений

Проблему, поставленную в заглавие, разделим на три.

Задачи

Источники

[4]. Утешев А.Ю., Калинина Е.А. Лекции по высшей алгебре. Часть II. Учеб. пособие. СПб. «СОЛО». 2007. 279 c.

[6]. Markoff A. On the determination of the number of roots of an algebraic equation situated in a given domain. Мат. сборник. 1940. Т. 7(49), N 1, c. 3–6. Текст ☞ ЗДЕСЬ (pdf)

Источник