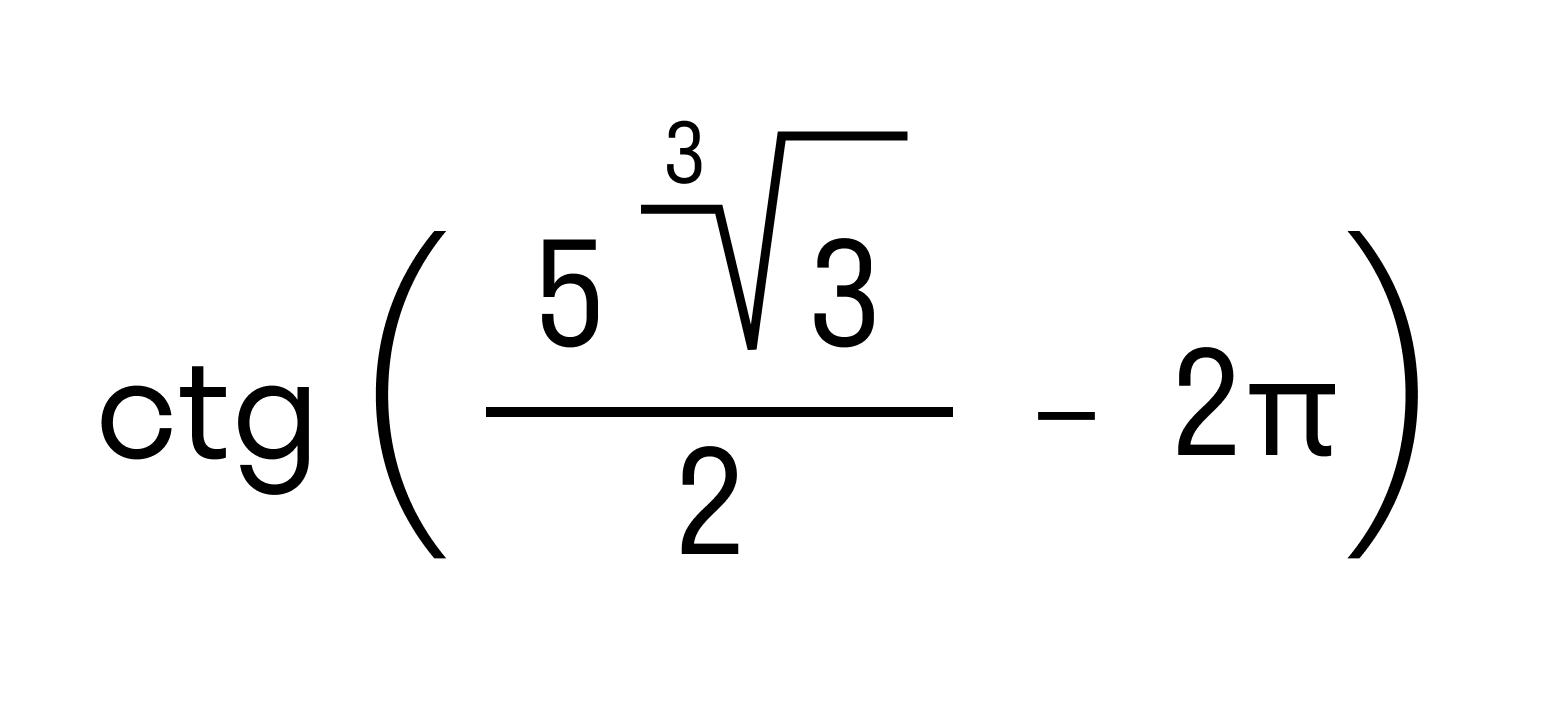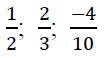Что такое вещественные числа в математике

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

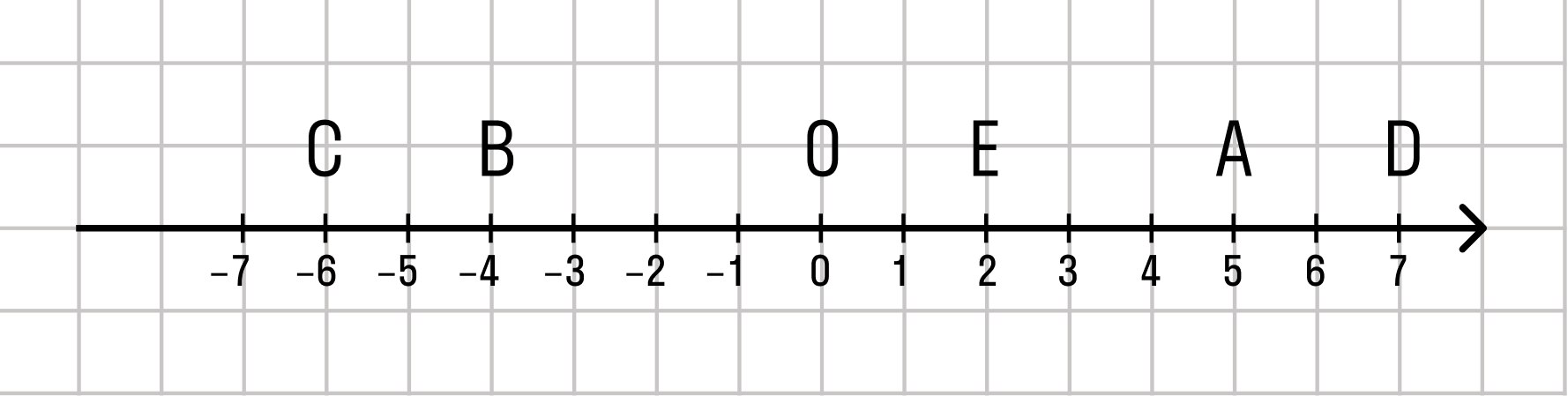
Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Числа. Действительные числа.

Вещественное, или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.

Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых иррациональные числа.

Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой. Вещественные числа состоят из простых объектов: целых и рациональных чисел.

Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.

Бесконечная десятичная дробь, это десятичная дробь, у которой после запятой есть бесконечное число цифр.

Числа, которые нельзя представить в виде , являются иррациональными числами.

Пример:

Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.

Рациональные и иррациональные числа создают множество действительных чисел. Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая.

Для числовых множеств используются обозначения:

Теория бесконечных десятичных дробей.

Вещественное число определяется как бесконечная десятичная дробь, т.е.:

где ± есть один из символов + или −, знак числа,

a₀ — целое положительное число,

a₁,a₂,…a_n,… — последовательность десятичных знаков, т.е. элементов числового множества <0,1,…9>.

Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:

Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно. Например, предположим даны 2 положительны числа:

Если a₀0, то α b₀ то α>β. Когда a₀=b₀ переходим к сравнению следующего разряда. И т.д. Когда α≠β, значит после конечного количества шагов встретится первый разряд n, такой что a_n≠b_n. Если a_nn, то α b_n то α>β.

Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например, суммой вещественных чисел α и β является вещественное число α+β, которое удовлетворяет таким условиям:

Аналогично определяет операция умножения бесконечных десятичных дробей.

Источник

Вещественные числа

Содержание

Натуральные числа [ править ]

Множество натуральных чисел [math] \mathbb N = \<1, 2, 3, \ldots\>[/math] определяется следующим образом:

Натуральные числа — первичные элементы, природа которых не обсуждается, все остальное базируется на этом.

Целые числа [ править ]

Рациональные числа [ править ]

Множество рациональных чисел [math] \mathbb Q = \ <\frac mn | m \in \mathbb Z, n \in \mathbb N \>[/math]

Множество рациональных чисел упорядочено, то есть всегда выполняется только один из трех случаев: [math] r \lt q, r = q[/math] или [math] r \gt q [/math]

Модуль [ править ]

Аксиома Архимеда [ править ]

В множестве [math] \mathbb Q [/math] выполняется аксиома Архимеда:

[math] 0 \lt r \lt q \\ r, q \in \mathbb Q \Rightarrow \\ \exists n \in \mathbb N : q \lt n \cdot r [/math]

Дополнение множества рациональных чисел [ править ]

Пусть [math]A, B[/math] — два числовых множества.

Неполнота числовой оси [ править ]

Тогда [math] \nexists d \in \mathbb Q : A \le d \le B [/math]

Случай [math] d^2=2 [/math] невозможен. Докажем это.

1) Для всех рациональных [math] \delta \in (0; 1): [/math]

[math] (d + \delta)^2 = d^2 + 2d\delta + \delta^2 \\ \delta^2 \lt \delta \Rightarrow (d + \delta)^2 \lt d^2 + 2d\delta + \delta = d^2 + (2d+1)\delta [/math]

[math] \delta_0 \in \mathbb Q; \delta_0 = \min<(\frac<1><3>, \frac<2-d^2><2d+1>)> \in (0; 1) [/math] ;

Для такого [math] \delta_0: (d + \delta_0)^2 \lt 2 \Rightarrow (d + \delta_0) \in A [/math]

2) Пусть [math] d^2 \gt 2 [/math] Для всех рациональных [math] \delta \in (-1; 0): [/math] [math] (d + \delta)^2 = d^2 + 2d\delta + \delta^2 \gt d^2 + 2d\delta + \delta[/math]

Этим утверждением обнаруживается серьезный пробел во множестве рациональных чисел. Для его ликвидации вводятся некоторые объекты. При таком пополнении должны выполняться:

Из разбора ясно, что мы стоим на аксиоматических позициях.

Для анализа важно то, что для [math] \mathbb R [/math] выполняется аксиома непрерывности.

Существует несколько моделей построения [math] \mathbb R [/math] :

Базируясь на аксиоме Архимеда и непрерывности, можно установить, что [math] \mathbb Q [/math] всюду плотно на [math] \mathbb R [/math] :

В любом вещественном интервале [math] (a, b) : (x: a \lt x \lt b) [/math] найдется рациональное число.

Для нас этот факт важен тем, что он гарантирует единственность пополнения [math] \mathbb Q [/math] для выполнения аксиомы непрерывности.

Любое такое пополнение, независимо от модели, приводит к множествам, изоморфным друг другу.

Источник

01.2. Вещественные числа и их свойства

Множество вещественных чисел является бесконечным. Оно состоит из рациональных и иррациональных чисел. Рациональ­ным называется число вида P/Q, где Р и Q — целые числа. Вся­кое вещественное число, не являющееся рациональным, назы­вается Иррациональным. Всякое рациональное число либо является целым, либо представляет собой конечную или пери­одическую бесконечную десятичную дробь. Например, рацио­нальное число 1/9 можно представить в виде 0,11111. Иррациональное число представляет собой бесконечную неперио­дическую десятичную дробь; примеры иррациональных чисел:

= 1,41421356. ; = 3,14159265.

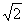
Сведения о вещественных числах могут быть кратко сис­тематизированы в виде перечисления их свойств.

А. Сложение и умножение вещественных чисел

Для любой пары вещественных чисел А и B определены единственным образом два вещественных числа а + B и а ∙ B, Называемые соответственно их Суммой и Произведением. Для любых чисел А, b и С имеют место следующие свойства.

4. Существует единственное число 0, такое, что а + 0 = a для любого числа а.

5. Для любого числа а существует такое число (-а), что а + (-а) = 0.

6. Существует единственное число 1 ≠ 0, Такое, что для любого числа а имеет место равенство

7. Для любого числа а ≠ 0 существует такое число а-1, что а ∙ а-1 = 1. Число а-1 обозначается также символом .

В. Сравнение вещественных чисел

Для любых двух вещественных чисел имеет место одно из трех соотношений: А = b (А равно B), а > b (А больше B) или А b и b > с, то а > с.

9. Если а > b, то а + с > b + с.

10. Если а > 0 и b > 0, то а b > 0

Источник

Виды чисел.

У нас есть числа натуральные, целые, рациональные и иррациональные, а также вещественные или действительные и еще есть другие, но в школьной программе в основном используют эти числа.

Натуральные числа ( N ) − это числа, используемые для счета предметов. Нуль не является натуральным числом.
Например: 1; 2; 3; 132; 168; 326; 548; 10050…

Целые числа ( Z ) — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (−) натуральных чисел.
Например: …−3; −2; 1; 0; 548; 10050…

Рациональные числа ( Q ) – это положительные и отрицательные числа можно представить в виде обыкновенной несократимой дроби вида: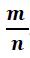

где m−целое число (числитель), n – натуральное число (знаменатель).
Например:

Иррациональные числа ( I ) − числа, которые не представимыми в виде дроби вида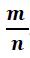

Например: √2; √5; π; e

Вещественные (действительные) числа ( R ).
Рациональные числа и иррациональные числа образуют множество действительных чисел.
Изобразим это множество чисел в виде рисунка:

Видно их вложенность друг в друга.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Источник