Что такое вес в геодезии
Геодезия
Для студентов аспирантов и преподавателей
Разделы
Определение веса измеряемых величин
Достоверность и точность уравненных элементов геодезической сети во многом зависит от правильности установления реального веса каждой измеряемой величины. В общем случае вес каждой непосредственно измеренной величины должен вычисляться по формуле
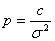
где с — постоянная для сети безразмерная величина (c=const), устанавливаемая до некоторой степени произвольно; 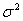
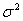
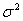
На стадии проектирования средние квадратические ошибки т измеряемых величин задают с учетом имеющегося опыта измерений таких величин в ранее построенных геодезических сетях. В этом случае вес запланированных к измерению в проектируемой сети горизонтальных направлений N, азимутов а, расстояний s вычисляют по формулам
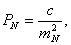
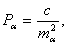
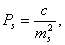
Горизонтальные направления на пунктах геодезической сети каждого данного класса измеряются равноточно. Поэтому целесообразно принять с=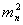
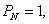
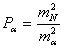
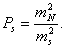
Средние квадратические ошибки измеренных направлений, азимутов, длин сторон можно найти разными способами и получить соответственно разные значения ошибки для одной и той же величины. Например, ошибку измеренного угла в триангуляции можно найти из уравнивания угловых измерений на станции (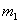
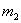
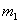
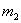
Известно, что совокупное влияние случайных и систематических ошибок на результаты измерений однородных величин наиболее полно сказывается на величинах свободных членов условных уравнений. Поэтому, чтобы получить средние квадратические ошибки, характеризующие реальную точность измерений, следует использовать невязки (свободные члены) условных уравнений.
В триангуляции среднюю квадратическую ошибку измеренного угла вычисляют по невязкам треугольников, используя формулу Ферреро
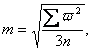
где п — число невязок со треугольников;
средняя квадратическая ошибка измеренного направления равна
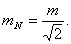
Для определения 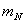
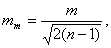
где п — число измерений, т. е. невязок треугольников в данном случае.
При свето- и радиодальномерных измерениях расстояний среднюю квадратическую ошибку 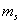
где а0 и а1 — эмпирические коэффициенты. Они указываются в паспорте прибора, а определяются из обработки измерений расстояний разной длины на эталонном полигоне. Однако практика показывает, что реальная точность измерений расстояний далека от величины, получаемой по формуле (5.9).
Наиболее достоверное значение средней квадратической ошибки измерения расстояний в сетях трилатерации и в линейно-угловых сетях можно вычислить по свободным членам со условных уравнений центральных систем и геодезических четырехугольников с измеренными в них длинами сторон:
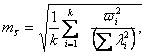
где 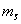
средней длины 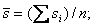
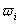
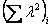
Если известны 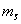
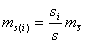
Формулы (5.10) и (5.11) дают несравненно более точные результаты, чем формула (5.9), поэтому их следует применять при вычислении по формулам (5.4) или (5.5) веса измеренных сторон.
Среднюю квадратическую ошибку определения астрономических азимутов на пунктах Лапласа вычисляют обычно по отклонениям значений азимута в приемах от его среднего значения. Величина полученной таким образом ошибки 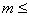
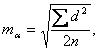
где п — число разностей d; в среднем тa =1,0″, что достаточно хорошо согласуется с другими оценками, полученными, например, при уравнивании обширных блоков астрономо-геодезической сети ( тa 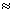
Вопросы надежной оценки точности измерений каждой базисной стороны и каждого азимута на пунктах Лапласа (не по сходимости результатов измерений в приемах) нуждаются в дальнейшем изучении и решении.
Неравноточные измерения. Вес измерений
Если измерения выполнялись не в одинаковых условиях, то результаты нельзя считать одинаково надежными. Такие измерения называют неравноточными. Например, один и тот же угол можно измерить точным и техническим теодолитом. Результаты данных измерений будут неравноточными.
Мерой сравнения результатов при неравноточных измерениях, т.е. мерой относительной ценности полученных неравноточных результатов является вес результата измерения.
Вес выражает как бы степень доверия, оказываемого данному результату по сравнению с другими результатами.
Чем надежнее результат, тем больше его вес.
Вес измерения – это отвлеченное число, обратно пропорциональное квадрату СКП (среднеквадратическая погрешность)результата измерения.
P = К / m2,
где P – вес результата измерения,
К – произвольное постоянное число для данного ряда измерений,
m – СКП (среднеквадратическая погрешность)результата измерения.
Из формулы видно, что чем меньше СКП измерения, тем оно точнее и его вес больше.
Отношение весов двух измерений обратно пропорционально квадратам СКП этих измерений, т.е.:
Если имеется ряд измерений l1, l2, …, ln, то очевидно, что вес одного измерения будет меньше веса среднего арифметического этих значений, т.е.:
A0 = (a1P1 + a2P2 + … + anPn) / (P1 + P2 + … +Pn),
где A0 – общая арифметическая середина,
ai – результат отдельно взятого измерения,
Pi – вес отдельно взятого измерения.
СКП любого результата измерения равна погрешности измерения с весом 1, делимой на корень квадратный из веса этого результата, т.е.:
где m – СКП любого результата измерения;
M – погрешность измерения с весом 1;
P – вес данного результата измерения.
СКП (среднеквадратическая погрешность) измерения с весом 1 равна корню квадратному из дроби, в числителе которой – сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
n – число измерений.
Геодезические сети.
Геодезической сетью называют систему закрепленных на местности точек земной поверхности, положение которых определено в общей для них системе координат и высот. Точки, относящиеся к геодезической сети называют геодезическими пунктами.
Геодезические сети могут создаваться как на малых, так и на огромных площадях земной поверхности. По территориальному признаку их можно подразделить на глобальную (общеземную) геодезическую сеть, покрывающую весь земной шар; национальные (государственные) геодезические сети, создаваемые в пределах территории каждой отдельной страны в единой системе координат и высот, принятой в данной стране; сети сгущения, предназначенные для создания съемочного обоснования топографических съемок; местные геодезические сети, т. е. сети на локальных участках, используемые для решения различных задач в местной системе координат.
Геодезические сети подразделяются на плановые и высотные. Плановые сети служат для определения плановых координат геодезических пунктах Х и Y. Высотные для определения высот пунктов H. Геодезические пункты закреплены на местности по разному, временными и постоянными значками.
Виды геодезических сетей:
1) Государственные геодезические сети- главные сети, имеют большую протяжённость ими покрыта вся территория страны. Предназначены: являются основой для построения низших сетей, для решения научных задач.
2) Сети сгущения: предназначены для увеличения плотности пунктов на 1 площади.
3) Сети съёмочного обоснования на основе которых непосредственно производятся съёмки контуров и рельефа местности, инженерно-геодезические работы при строительстве сооружений.
4) Специальные сети, развиваемые при строительстве сооружений, представляющих к геодезическим работам специальные требования.
Плановые геодезические сети
Плановые сети служат для определения плановых координат геодезических пунктах Х и Y. Представляют собой совокупность пунктов, которые имеют исключительно горизонтальные координаты. Выполняются на плоскости, не требующей дополнительного нивелирования контрольных точек. Используются для составления кадастрового плана земельного участка и межевания территории.
Плановые геодезические сети подразделяются на три категории:
— государственные геодезические сети (ГГС),
— сети съёмочного обоснования (ССО).
Государственные геодезические сети и сети сгущения могут создаваться методами:
триангуляции (построение на местности примыкающих друг к другу треугольников, в которых измеряются все горизонтальные углы и длины сторон треугольника),
полигонометрии (построение на местности системы ломаных линий, называемых полигонометрическими ходами, которые в отдельных случаях замыкаются, образуя многоугольники, называемые полигонами),
Построение геодезических сетей производится по принципу «от общего к частному», от более крупных и точных построений к более мелким и менее точным.
Государственные геодезические сети по точности и назначению разделяются на четыре класса 1, 2, 3, 4 классы.
Веса результатов измерений и их функций
Вес результата измерения определяют по формуле

где 

Вес – относительная характеристика точности, т.е. он дает представление о точности результата измерения только при сравнении с весами других результатов измерений в данной задаче.
В качестве единицы меры дисперсий принимают СКП измерения 
Подставив в (3.11) вместо 
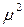



Величину 
Заменив в формуле (3.6) величины 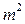
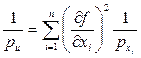
Таким образом, методика определения весов функций измеренных величин такая же, что и при вычислении СКП функций измеренных величин. Формулы для определения весов функций получаются из формул для СКП тех же функций заменой величин 

Порядок вычисления веса функции измеренных величин следующий:
1) записывается функция в буквенном выражении;
2) определяется обратный вес этой функции по вышеизложенным правилам;
3) осуществляется переход от обратного веса к весу.
Эта тема принадлежит разделу:
Геодезия
Государственный университет по землеустройству.. кафедра геодезии и геоинформатики..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Веса результатов измерений и их функций
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Все темы данного раздела:
Дополнительная
4. Батраков Ю.Г. Геодезические сети специального назначения. М.; Картгеоцентр – Геодезиздат, 1999. 5. Инструкция по развитию съемочного обоснования и съемке ситуации и рельефа с применение
Вычислительная обработка тахеометрического хода
По данным полевого журнала тахеометрической съемки (табл. 2.1.) вычислить и занести в журнал для каждой станции среднее значение горизонтального угла, место нуля МО, углы на
Журнал тахеометрической съемки
Станция 216 i = 1,40 м Нст. = Положение вертикального круга № точек наблю-дений Расстояние по дальномеру D’=100
Вычисление координат точек тахеометрического хода
В “Ведомость вычисления координат” из журнала тахеометрической съемки (табл.2.1.) выписать средние значения горизонтальных углов и средние значения горизонтальных проложений сторон
Вычисление высот точек тахеометрического хода
В «Ведомость вычисления высот точек тахеометрического хода» (табл. 2.2.) выписать: – из табл. 1 высоты исходных пунктов
Вычисление высот съемочных пикетов
Из «Ведомости вычисления высот точек тахеометрического хода» (табл. 2.2.) выписать в журнал тахеометрической съемки высоты точек хода. Вычислить последовательно углы наклон
Составление плана участка
На чертежной бумаге размером 3545 см построить координатную сетку со сторонами 10 с
Вопросы для самопроверки
1. Какова цель тахеометрической съемки? 2. Как определяют при тахеометрической съемке плановое положение съемочных пикетов и их высоты? 3. В чем различие между абр
Рекомендации по обработке вычислений
Для выполнения контрольной работы по теме «Теория погрешностей измерений» необходимо решить около тридцати контрольных задач. Контрольная работа выполняется в соответствии с вариантами, у
Решение.
Результаты расчетов сведены в таблицу 3.1 (табличная форма). Табл. 3.1 № п/п Результаты измерений
Задача 1.
Для исследования точности измерения горизонтального угла полным приемом теодолитом 3Т5КП, им был многократно измерен угол. Результаты оказались следующими: 39°17,4′; 39º 16,8′; 39°
Задача 2.
Дана совокупность угловых невязок в треугольниках объемом 50 единиц. На данной совокупности проверить свойства случайных погрешностей. Считая невязки истинными погрешностями, вычислить СКП и прои
Оценка точности функции измеренных величин
На содержание этого раздела следует обратить особое внимание и учесть порядок определения СКП функции, вычисляемой по измеренным величинам (аргументам) с СКП, связанными с искомой в
Решение.
Для определения погрешности дирекционного угла последней линии, прежде всего, необходимо представить этот дирекционный угол как функцию исходных и измеренных величин. Так как были измерены п
Задача 4.
Линия теодолитного хода измерена частями с СКП
Задача 6.
Вычислить превышение, полученное тригонометрическим нивелированием, и его предельную погрешность, если расстояние, измеренное нитяным дальномером D =210,5м с СКП
Задача 10.
В треугольнике измерены две стороны и
РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке ряда равноточных измерений одной и той же величины вычисляют: 1) среднеарифметическое значение измеренной величины (как наиболее надежное)
Решение.
Дирекционный угол последней линии теодолитного хода вычисляем по известной формуле Условие
Решение.
Длина определяется соотношением
Задача 18.
Чему равен вес среднеарифметического значения угла, полученного из =. приемов (см. приложение табл. 2)?
НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке неравноточных измерений одной и той же величины решаются последовательно следующие задачи: 1) определяют средневесовое значение из результатов
Задача 24.
По четырем теодолитным ходам на узловую линию передан дирекционный угол. Число горизонтальных углов поворота в каждом ходе различно. Произвести математическую обработку результатов значений дирек
Задача 25.
По четырем ходам геометрического нивелирования с различным числом станций была передана высота на узловой репер, что дало результаты (см. приложение табл. 2): № п
Задача 26.
В таблице приведены невязки в полигонах геометрического нивелирования и периметры полигонов. Оценить точность нивелирования. № пол-ов
Задача 27.
Произвести оценку точности измерения горизонтальных углов в замкнутом теодолитном ходе по невязкам в полигонах. № полигонов Число углов в поли
Задача 28.
По невязкам в треугольниках сети триангуляции произвести оценку точности угловых измерений. № треугольников Невязки
Округление приближенных чисел
В приближенных вычислениях часто приходиться округлять числа (как приближенные, так и точные), т. е. отбрасывать одну или несколько последних цифр. Чтобы обеспечить наибольшую близо
Погрешности измерений
Точность измерений характеризуется погрешностями измерений. Погрешностью измерения называют разность между изм
Вопросы для самопроверки
1. Какие измерения называют равноточными? 2. Что называется погрешностью измерений? 3. Как классифицируются погрешности измерений? 4. Какими свойствами обладают случайные
Общая постановка задачи
Если плотность пунктов опорной плановой геодезической сети недостаточна для выполнения топографических съемок, то сеть сгущают путем развития планово-высотного съемочного обосновани
Исходные данные
Схема сети и результаты полевых измерений показаны на рис. 4.1. В соответствии с вариантом индивидуального задания (см. табл. 4 приложения), на схеме изменяют значения длины линии и
Последовательность выполнения работы
Составляют схематический чертеж согласно заданному варианту. Уравнивание углов выполняется в следующем порядке. 4.3.1. Выбирают узловую линию, т.е. линию, примыкающую к узл
Вопросы для самопроверки
1. По какой формуле вычисляется дирекционный угол узловой линии при передаче его от исходной стороны по ходу с левыми (правыми) углами? 2. По какой формуле вычисляется окончательное значе
Основные правила дифференцирования
Производная –этопредел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую конечную производную, называют диффер
