Что такое вершины математика 5 класс

Многоугольники

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Источник

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

— наглядные представления о фигурах на плоскости;

— изображение геометрических фигур.

Многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Периметр многоугольника – это сумма всех его сторон.

Диагональ многоугольника – это отрезок, соединяющий две несмежные вершины многоугольника.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мы уже знаем, из каких элементов состоят некоторые геометрические фигуры и как их изобразить на плоскости. Сегодня мы рассмотрим многоугольник.

Ломаная линия лежит в основе построения многоугольника.

Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.

Отрезки АВ, ВС, СD,DE называются звеньями ломаной. У ломаной, которую мы изобразили, четыре звена.

Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.

Измерим длину ломаной.

Сумма длин всех звеньев равна:

АВ + ВС + СD + DЕ = 14 см – длина ломаной

Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.

Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.

Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.

∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника

Точки А, В, С, D, E – вершины многоугольника

Кроме того, у многоугольника есть ещё и диагонали.

Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.

Сумма всех сторон многоугольника составляет периметр многоугольника.

P = АВ + ВС + СD + DЕ + ЕА

Рассмотрим разновидности многоугольников.

Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.

Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.

Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.

Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Для определения площади многоугольника надо выяснить, сколько раз выбранная единица измерения содержится в этой фигуре.

Не только человек может рисовать многоугольники. Природа тоже создаёт многоугольники в большом разнообразии. Рассмотрим, где они встречаются. Например, шестиугольники можно увидеть в сотах пчёл и – под микроскопом – в строении глаза мухи или некоторых других насекомых.

Панцирь черепахи тоже изобилует большим количеством многоугольников. Как и кожа змеи: она буквально покрыта многоугольниками. В общем, природа постаралась и разнообразила мир геометрическими фигурами.

№ 1. Чему равен периметр правильного шестиугольника со стороной 4 см?

Решение: для решения этой задачи достаточно вспомнить, что в правильных фигурах все стороны равны, следовательно, все стороны шестиугольника равны 4 см. Вычислим периметр шестиугольника, это сумма всех его сторон.

Р = 4 см + 4 см + 4 см + 4 см + 4 см + 4 см = 24 см

№ 2. Из листа железа размером 10 × 14 см вырезали два квадрата со стороной 4 см и три прямоугольника со сторонами 2см и 6см. Определите площадь остатка.

Решение: сначала найдём площадь листа:

S = 10 cм · 14 см = 140 см 2

Далее вычислим площадь квадратов со сторонами 4см:

S = 4 cм · 4 см = 16 см 2

Тогда площадь двух квадратов равна:

16 см 2 · 2 = 32 см 2

Найдём площадь прямоугольника:

S = 2 cм · 6 см = 12 см 2

Тогда площадь трёх прямоугольников равна:

12 см 2 · 3 = 36 см 2

Определим площади всех квадратов и прямоугольников, вырезанных из листа:

32 см 2 + 36 см 2 = 68 см 2

А теперь найдём площадь остатка: 140 см 2 – 68 см 2 = 72 см 2

Источник

Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями

Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Простейшие четырёхугольники

Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.

Наиболее часто приходится сталкиваться со следующими видами:

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.

Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.

Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Треугольный многоугольник

Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.

В зависимости от особенностей, фигура может называться:

Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.

Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.

Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.

Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Теорема об углах

Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.

Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник

Мерзляк 5 класс — § 13. Многоугольники. Равные фигуры

Вопросы к параграфу

1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.

3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.

4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.

5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.

6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.

Решаем устно

1. Сумму чисел 24 и 18 уменьшите на 33.

(24 + 18) — 33 = 42 — 33 = 9

2. Разность чисел 30 и 14 увеличьте в 3 раза.

3. Произведение чисел 12 и 5 увеличьте на 19.

(12 • 5) + 19 = 60 + 19 = 79

4. Частное чисел 189 и 9 уменьшите в 7 раз.

(189 : 9) : 7 = 21 : 7 = 3

5. Укажите среди данных отрезков равные, если:

Ответ: АВ = TQ и EF = MN.

Упражнения

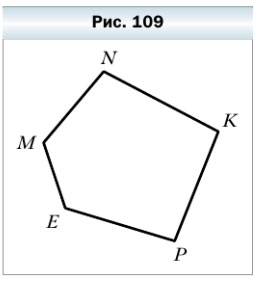
321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

Периметр многоугольника равен сумме длин его сторон.

2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.

324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.

Периметр многоугольника равен сумме длин его сторон.

8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.

1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.

2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.

3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.

4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.

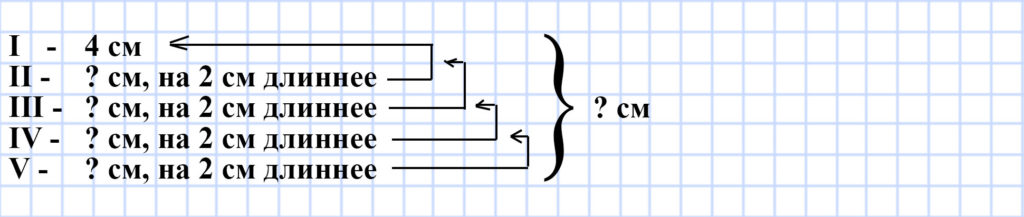
328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.

2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.

3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.

4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.

5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.

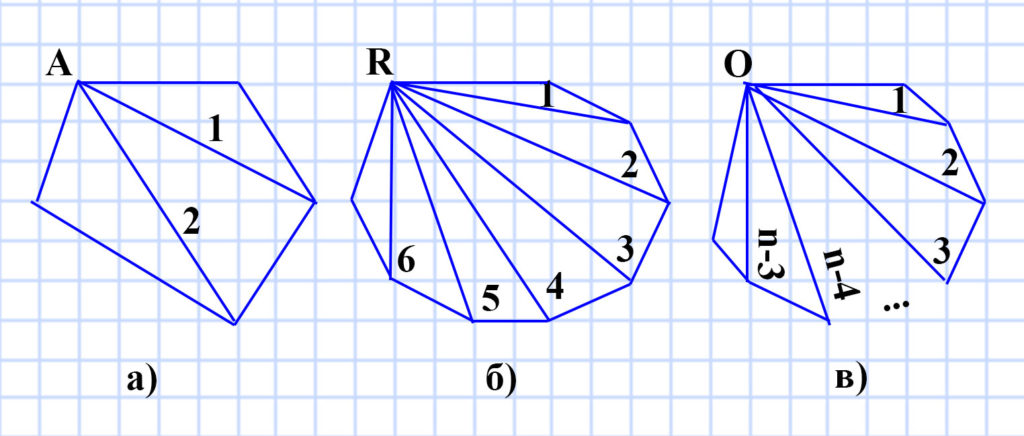
329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?

а) Из одной вершины пятиугольника можно провести 2 диагонали.

б) Из одной вершины девятиугольника можно провести 6 диагоналей.

в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:

2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?

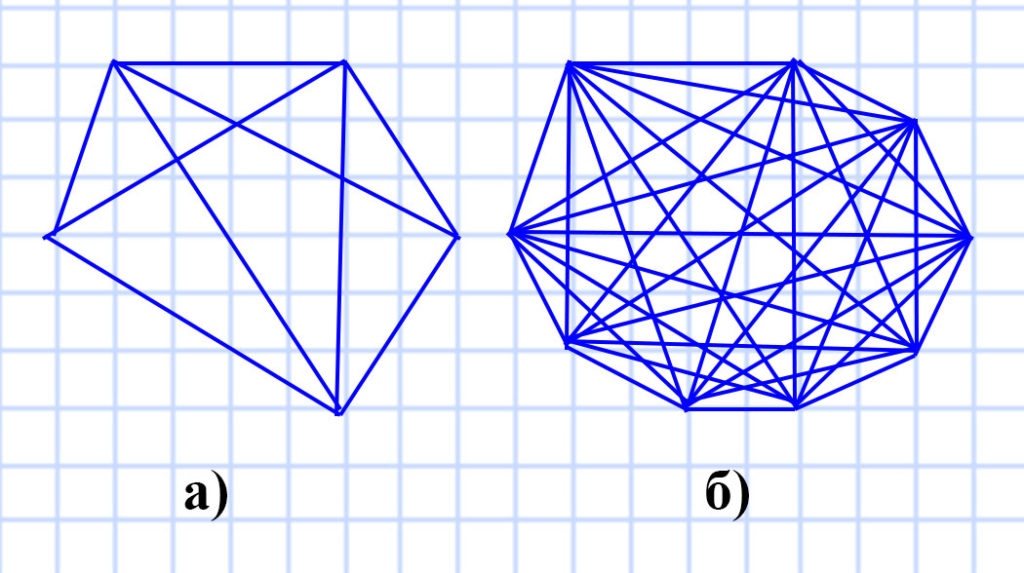
а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.

б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.

в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:

Ответ: 5, 27, n • (n-3) : 2.

330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?

Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:

331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:

а) 19°

Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:

Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:

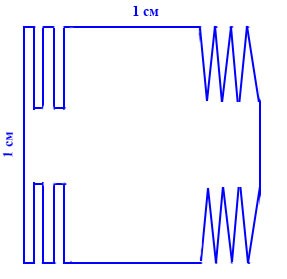
332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.

В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.

Упражнения для повторения

333. Сравните:

1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г

2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см

3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм

4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг

334. Выполните сложение, выбирая удобный порядок вычислений:

1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927

2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898

3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300

4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400

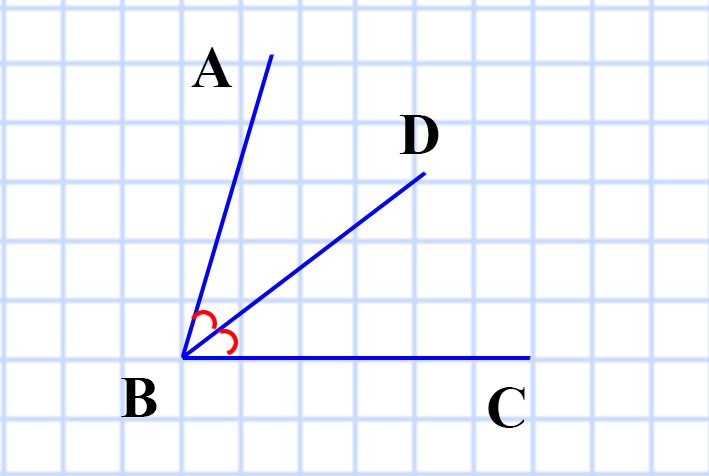
335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.

Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:

∠DBC = ∠ABC : 2 = 74° : 2 = 37°

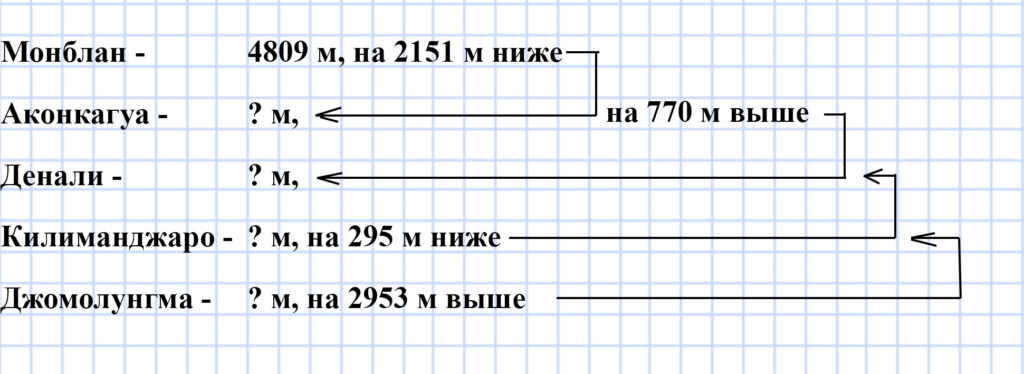
336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?

1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.

2) 6 960 — 770 = 6 190 (м) — высота горы Денали.

3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.

4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.

Ответ: 8 848 метров.

Задача от мудрой совы

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.

Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.

Под заданные условия подходит только число 5.

Источник